Wasserfluss
Storyboard 
In gesättigtem Boden können Situationen auftreten, in denen Druckschwankungen auftreten. Diese Schwankungen wiederum erzeugen einen Fluss, der in diesem Fall innerhalb der Bodenporen stattfinden sollte. Da diese Poren im Bereich von Mikrometern oder zehn Mikrometern liegen, neigt der Fluss aufgrund der niedrigen Reynoldszahlen dazu, laminar zu sein.
ID:(369, 0)
Flussdichtelösung aus einem Kanal
Bild 
Die erhaltene Lösung für die Höhe und die Parameter der Strömung an einem Referenzpunkt ($j_{s0}$) und die Referenzhöhe der Wassersäule ($h_0$) zeigt uns, dass die Flussdichte ($j_s$) gleich ist:
| $ \displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{1}{\sqrt{1 - \displaystyle\frac{ 2 x }{ s_0 }}} $ |
Wir können die Flussdichte ($j_s$) graphisch in Bezug auf die zusätzlichen Faktoren $j_s/j_{s0}$ und $x/x_0$ wie folgt darstellen:
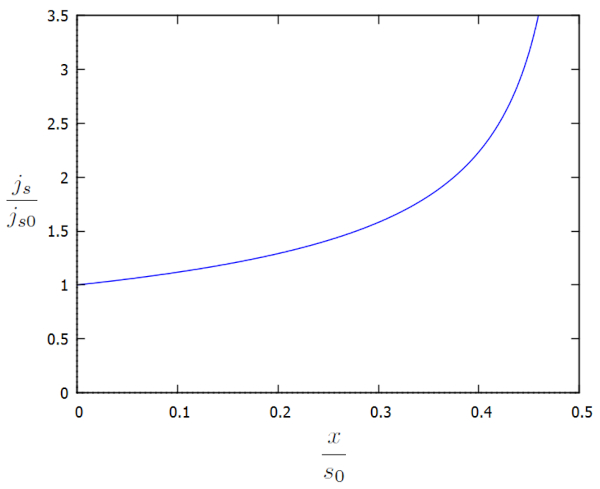
die Flussdichte ($j_s$) steigt weiter an, wenn wir uns dem Kanal nähern, da die Höhe der Wassersäule am Boden ($h$) abnimmt. Dieser Anstieg ist notwendig, um die Fließgeschwindigkeit in die Flussdichte ($j_s$) aufrechtzuerhalten oder alternativ zu erhöhen.
ID:(7827, 0)
Laminare Strömung durch ein Rohr
Notiz 
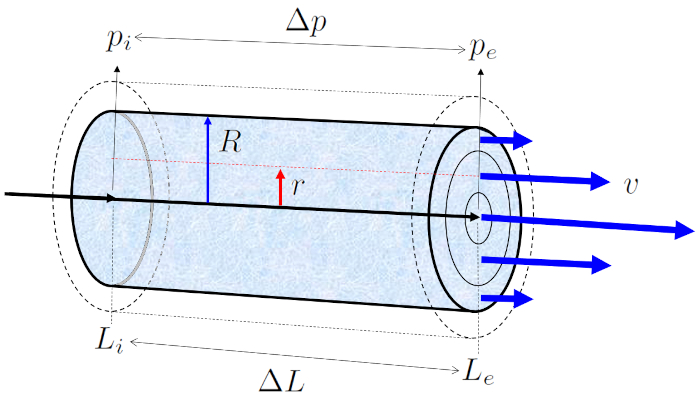
Wenn ein mit Flüssigkeit gefülltes Rohr mit einer Viskosität von ERROR:5422,0 Die Druck in der Ausgangsposition ($p_i$) bei der Position am Anfang des Rohres ($L_i$) und die Druck in Endlage (e) ($p_e$) bei der Positionieren am Ende des Rohres ($L_e$) ausgesetzt wird, entsteht entlang von der Rohrlänge ($\Delta L$) Eine Druckunterschied ($\Delta p_s$), was das Profil von die Geschwindigkeit auf einer Zylinder-Radio ($v$) ergibt:
Bei Strömungen mit niedrigen Werten von der Anzahl der Reynold ($Re$), wo die Viskosität bedeutender ist als die Trägheit der Flüssigkeit, entwickelt sich der Fluss laminar, das heißt ohne das Vorhandensein von Turbulenzen.
ID:(2218, 0)
Laminare im Strom
Zitat 
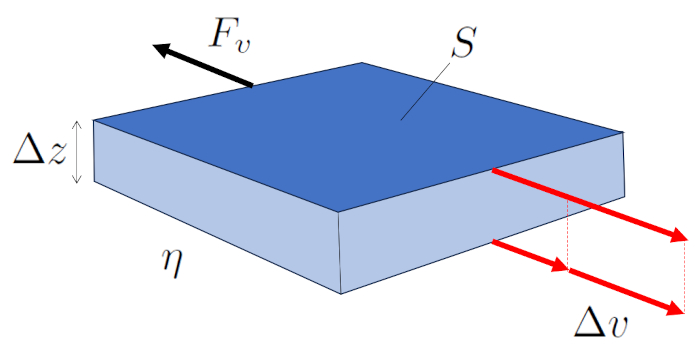
Im laminaren Fluss bewegen sich benachbarte Schichten, und zwischen ihnen wirkt eine durch die Viskosität erzeugte Kraft. Die schnellere Schicht zieht ihre langsamere Nachbarschicht mit, während die langsamere Schicht den Fortschritt der schnelleren einschränkt.
Daher ist die Kraft die Viscose Kraft ($F_v$), die von ERROR:10119.1 über die andere erzeugt wird, eine Funktion von ERROR:5556.1, ERROR:5436.1 und ERROR:5422.1, wie in der folgenden Gleichung dargestellt:
| $ F_v =- S \eta \displaystyle\frac{ \Delta v }{ \Delta z }$ |
illustriert im folgenden Diagramm:
ID:(7053, 0)
Durch einen Zylinder fließen
Übung 
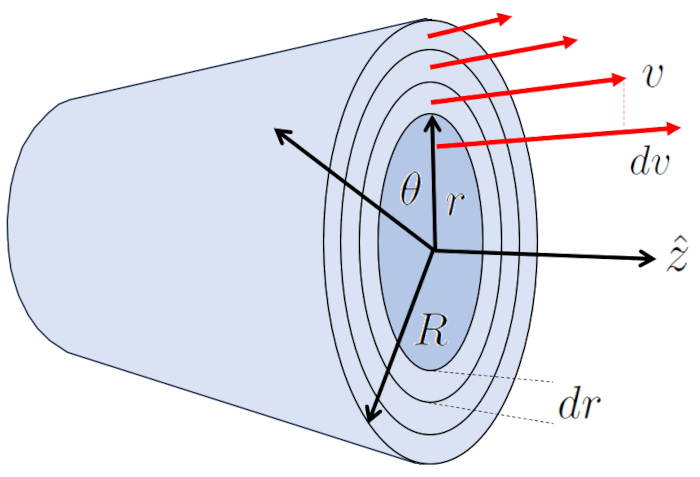
Der laminare Fluss um einen Zylinder kann als mehrere zylindrische Schichten dargestellt werden, die unter dem Einfluss benachbarter Schichten gleiten. In diesem Fall wird die Viscose Kraft ($F_v$) mit der Rohrlänge ($\Delta L$), die Viskosität ($\eta$) und den Variablen die Zylinder-Stern Position ($r$) und die Geschwindigkeit auf einer Zylinder-Radio ($v$) wie folgt ausgedrückt:
| $ F_v =-2 \pi r \Delta L \eta \displaystyle\frac{ dv }{ dr }$ |
Die Schicht am Rand bei ERROR:5417.1 bleibt aufgrund des Randeffekts stehen und verlangsamt durch die Viskosität ($\eta$) die benachbarte Schicht, die eine Geschwindigkeit hat.
Das Zentrum ist der Teil, der sich mit die Maximale Durchflussrate ($v_{max}$) bewegt und die umgebende Schicht mitzieht. Diese Schicht zieht wiederum die nächste Schicht und so weiter, bis sie die Schicht erreicht, die Kontakt mit der Zylinderwand hat, die sich nicht bewegt.
Auf diese Weise überträgt das System Energie von der Mitte zur Wand und erzeugt ein Geschwindigkeitsprofil, das wie folgt dargestellt wird:
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
mit:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
ID:(7057, 0)
Strömung nach Hagen-Poiseuillee Gleichung
Gleichung 
Das Profil von die Geschwindigkeit auf einer Zylinder-Radio ($v$) in der Positionsradius in einem Rohr ($r$) ermöglicht es uns, der Volumenstrom ($J_V$) in einem Rohr durch Integration über die gesamte Oberfläche zu berechnen, was zur bekannten Hagen-Poiseuille-Gesetz führt.
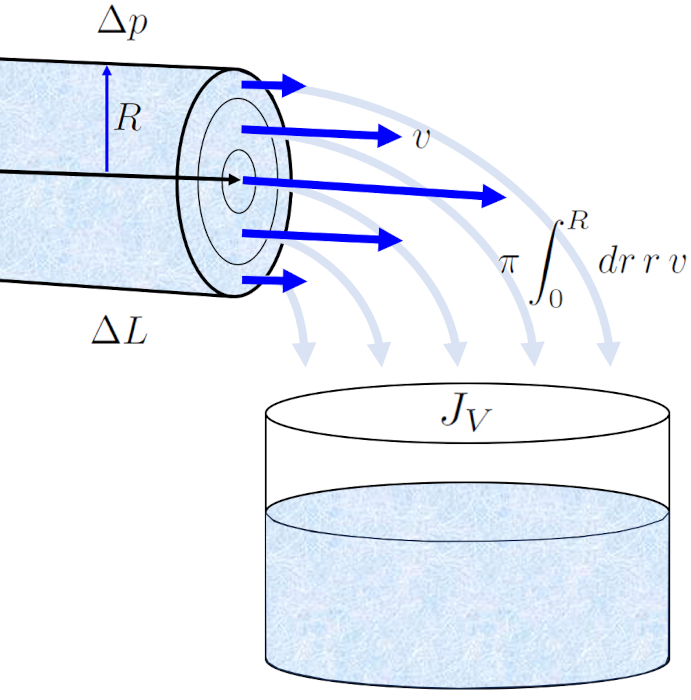
Das Ergebnis ist eine Gleichung, die von ERROR:5417,0 zur vierten Potenz abhängt. Es ist jedoch entscheidend zu beachten, dass dieses Strömungsprofil nur im Falle einer laminaren Strömung gültig ist.
Daraus ergibt sich mit die Viskosität ($\eta$), dass der Volumenstrom ($J_V$) vor ein Rohrlänge ($\Delta L$) und eine Variación de la Presión ($\Delta p$) die Ausdruck:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Die Originalarbeiten, die zu diesem Gesetz mit einem kombinierten Namen führten, waren:
![]() "Ueber die Gesetze, welche des der Strom des Wassers in röhrenförmigen Gefässen bestimmen", Gotthilf Hagen, Annalen der Physik und Chemie 46:423442 (1839).
"Ueber die Gesetze, welche des der Strom des Wassers in röhrenförmigen Gefässen bestimmen", Gotthilf Hagen, Annalen der Physik und Chemie 46:423442 (1839).
![]() "Recherches expérimentales sur le mouvement des liquides dans les tubes de très-petits diamètres" (Experimentelle Untersuchungen zur Bewegung von Flüssigkeiten in Röhren mit sehr kleinen Durchmessern), Jean-Louis-Marie Poiseuille, Comptes Rendus de l'Académie des Sciences 9:433544 (1840).
"Recherches expérimentales sur le mouvement des liquides dans les tubes de très-petits diamètres" (Experimentelle Untersuchungen zur Bewegung von Flüssigkeiten in Röhren mit sehr kleinen Durchmessern), Jean-Louis-Marie Poiseuille, Comptes Rendus de l'Académie des Sciences 9:433544 (1840).
ID:(2216, 0)
Volumenstrom
Script 
Während ein Abgelaufene Zeit ($\Delta t$) bewegt sich die Flüssigkeit mit eine Mittlere Geschwindigkeit der Flüssigkeit ($v$) um ein Rohrelement ($\Delta s$). Wenn die Abschnitt ($S$) die Menge an Flüssigkeit darstellt, die in der Abgelaufene Zeit ($\Delta t$) diesen Abschnitt durchquert, wird sie wie folgt berechnet:
$\Delta V = S \Delta s = Sv \Delta t$
Diese Gleichung besagt, dass das Volumen der Flüssigkeit, das während ein Abgelaufene Zeit ($\Delta t$) durch den Abschnitt die Abschnitt ($S$) fließt, gleich dem Produkt aus der Querschnittsfläche und der zurückgelegten Distanz der Flüssigkeit in dieser Zeit ist.
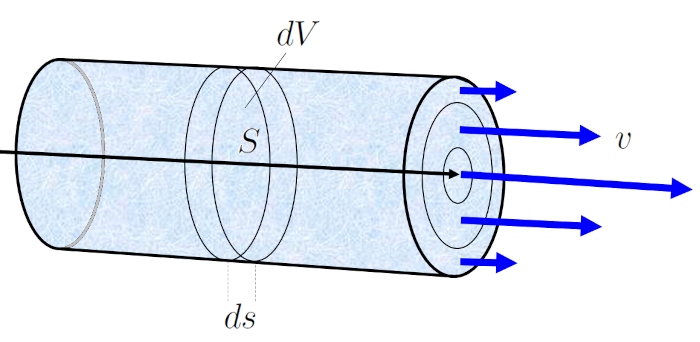
Dies erleichtert die Berechnung von der Volumenelement ($\Delta V$), dem Volumen der Flüssigkeit, das in einem bestimmten Zeitraum von der Abgelaufene Zeit ($\Delta t$) durch den Kanal fließt, entsprechend der Volumenstrom ($J_V$).
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
ID:(2212, 0)
Wasserfluss
Beschreibung 
In gesättigtem Boden können Situationen auftreten, in denen Druckschwankungen auftreten. Diese Schwankungen wiederum erzeugen einen Fluss, der in diesem Fall innerhalb der Bodenporen stattfinden sollte. Da diese Poren im Bereich von Mikrometern oder zehn Mikrometern liegen, neigt der Fluss aufgrund der niedrigen Reynoldszahlen dazu, laminar zu sein.
Variablen
Berechnungen
Berechnungen
Gleichungen
Wenn wir die Hydraulische Leitfähigkeit ($G_h$) betrachten, k nnen wir feststellen, dass der Z hler den Querschnitt des Rohrs enth lt, der als $\pi R^2$ dargestellt wird. Hier entspricht der Rohrradius ($R$) einer Eigenschaft der Fl ssigkeit, die Viskosität ($\eta$) steht im Zusammenhang mit der Viskosit t der Fl ssigkeit, und der Rohrlänge ($\Delta L$) bezieht sich auf den erzeugten Druckgradienten.
| $ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$ |
Somit kann der Faktor, der spezifisch f r die Geometrie der Poren ist, als die Hydrodynamische Permeabilität ($k$) mit der folgenden Formel definiert werden:
| $ k = \displaystyle\frac{ R ^2}{8}$ |
(ID 108)
Wenn wir das Profil von ERROR:5449,0 f r ein Fluid in einem zylindrischen Kanal betrachten, in dem die Geschwindigkeit auf einer Zylinder-Radio ($v$) in Abh ngigkeit von ERROR:10120,0 gem folgendem Ausdruck variiert:
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
unter Verwendung von der Rohrradius ($R$) und die Maximale Durchflussrate ($v_{max}$). K nnen wir die Maximale Durchflussrate ($v_{max}$) mithilfe von die Viskosität ($\eta$), die Druckunterschied ($\Delta p$) und der Rohrlänge ($\Delta L$) wie folgt berechnen:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Wenn wir die Geschwindigkeit ber den Querschnitt des Kanals integrieren, erhalten wir der Volumenstrom ($J_V$), definiert als das Integral von $\pi r v(r)$ bez glich ERROR:10120,0 von $0$ bis ERROR:5417,0. Dieses Integral kann wie folgt vereinfacht werden:
$J_V=-\displaystyle\int_0^Rdr \pi r v(r)=-\displaystyle\frac{R^2}{4\eta}\displaystyle\frac{\Delta p}{\Delta L}\displaystyle\int_0^Rdr \pi r \left(1-\displaystyle\frac{r^2}{R^2}\right)$
Die Integration f hrt zur resultierenden Hagen-Poiseuille-Gesetz:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
(ID 3178)
Der Volumenstrom ($J_V$) kann aus die Hydraulische Leitfähigkeit ($G_h$) und die Druckunterschied ($\Delta p$) unter Verwendung der folgenden Gleichung berechnet werden:
| $ J_V = G_h \Delta p $ |
Weiterhin, unter Verwendung der Beziehung f r die Hydraulic Resistance ($R_h$):
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
ergibt sich:
| $ \Delta p = R_h J_V $ |
(ID 3179)
Da die viskose Kraft gegeben ist als
| $ F_v =- S \eta \displaystyle\frac{ \Delta v }{ \Delta z }$ |
und die Oberfl che des Zylinders ist
$S=2\pi R L$
wobei $R$ der Radius und $L$ die L nge des Kanals ist, kann die viskose Kraft ausgedr ckt werden als
| $ F_v =-2 \pi r \Delta L \eta \displaystyle\frac{ dv }{ dr }$ |
wobei $\eta$ die Viskosit t repr sentiert und $dv/dr$ den Geschwindigkeitsgradienten zwischen der Wand und dem Fluss darstellt.
(ID 3623)
Wenn eine die Druckunterschied ($\Delta p_s$) auf einen Abschnitt mit einer Fl che von $\pi R^2$ wirkt, wobei der Rohrradius ($R$) als der Krümmung Radio ($r$) fungiert, erzeugt sie eine Kraft, die wie folgt dargestellt wird:
$\pi r^2 \Delta p$
Diese Kraft treibt die Fl ssigkeit gegen den Viskosewiderstand an, der durch folgenden Ausdruck gegeben ist:
| $ F_v =-2 \pi r \Delta L \eta \displaystyle\frac{ dv }{ dr }$ |
Durch das Gleichsetzen dieser beiden Kr fte erhalten wir:
$\pi r^2 \Delta p = \eta 2\pi r \Delta L \displaystyle\frac{dv}{dr}$
Dies f hrt zu folgender Gleichung:
$\displaystyle\frac{dv}{dr} = \displaystyle\frac{1}{2\eta}\displaystyle\frac{\Delta p}{\Delta L} r$
Wenn wir diese Gleichung von einer Position, die durch der Krümmung Radio ($r$) definiert ist, bis zum Rand, wo der Rohrradius ($R$) ist (unter Ber cksichtigung, dass die Geschwindigkeit am Rand null ist), integrieren, k nnen wir die Geschwindigkeit auf einer Zylinder-Radio ($v$) als Funktion von der Krümmung Radio ($r$) erhalten:
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
Dabei ist:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
die Maximale Durchflussrate ($v_{max}$) in der Mitte des Flusses.
(ID 3627)
Da die Hydraulic Resistance ($R_h$) gem der folgenden Gleichung gleich die Hydraulische Leitfähigkeit ($G_h$) ist:
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
und da die Hydraulische Leitfähigkeit ($G_h$) wie folgt in Bezug auf die Viskosität ($\eta$), der Rohrradius ($R$) und der Rohrlänge ($\Delta L$) ausgedr ckt wird:
| $ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$ |
k nnen wir folgern, dass:
| $ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$ |
(ID 3629)
(ID 3804)
Der Fluss wird als das Volumen der Volumenelement ($\Delta V$) geteilt durch die Zeit der Abgelaufene Zeit ($\Delta t$) definiert, was durch die folgende Gleichung ausgedr ckt wird:
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
und das Volumen ist das Produkt der Querschnittsfl che die Rohr Sektion ($S$) mit dem zur ckgelegten Weg der Rohrelement ($\Delta s$):
| $ \Delta V = S \Delta s $ |
Da der zur ckgelegte Weg der Rohrelement ($\Delta s$) pro Zeiteinheit der Abgelaufene Zeit ($\Delta t$) der Geschwindigkeit entspricht, wird dies durch die folgende Gleichung dargestellt:
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Somit ist der Fluss eine Flussdichte ($j_s$), der mit der folgenden Gleichung berechnet wird:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
(ID 4349)
Die Definition von der Volumenstrom ($J_V$) ist der Volumenelement ($\Delta V$) w hrend der Abgelaufene Zeit ($\Delta t$):
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
was im Grenzfall eines infinitesimal kleinen Zeitintervalls der Ableitung von der Volume ($V$) bez glich der Zeit ($t$) entspricht:
| $ J_V =\displaystyle\frac{ dV }{ dt }$ |
(ID 12713)
(ID 14459)
Wenn wir das Hagen-Poiseuille-Gesetz betrachten, das es uns erm glicht, der Volumenstrom ($J_V$) aus der Rohrradius ($R$), die Viskosität ($\eta$), der Rohrlänge ($\Delta L$) und die Druckunterschied ($\Delta p$) zu berechnen:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
k nnen wir die Hydraulische Leitfähigkeit ($G_h$) einf hren, das in Bezug auf der Rohrlänge ($\Delta L$), der Rohrradius ($R$) und die Viskosität ($\eta$) definiert ist:
| $ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$ |
um zu folgendem Ergebnis zu gelangen:
| $ J_V = G_h \Delta p $ |
(ID 14471)
Beispiele
(ID 15202)
Die erhaltene L sung f r die H he und die Parameter der Strömung an einem Referenzpunkt ($j_{s0}$) und die Referenzhöhe der Wassersäule ($h_0$) zeigt uns, dass die Flussdichte ($j_s$) gleich ist:
| $ \displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{1}{\sqrt{1 - \displaystyle\frac{ 2 x }{ s_0 }}} $ |
Wir k nnen die Flussdichte ($j_s$) graphisch in Bezug auf die zus tzlichen Faktoren $j_s/j_{s0}$ und $x/x_0$ wie folgt darstellen:

die Flussdichte ($j_s$) steigt weiter an, wenn wir uns dem Kanal n hern, da die Höhe der Wassersäule am Boden ($h$) abnimmt. Dieser Anstieg ist notwendig, um die Flie geschwindigkeit in die Flussdichte ($j_s$) aufrechtzuerhalten oder alternativ zu erh hen.
(ID 7827)
Wenn ein mit Fl ssigkeit gef lltes Rohr mit einer Viskosit t von ERROR:5422,0 Die Druck in der Ausgangsposition ($p_i$) bei der Position am Anfang des Rohres ($L_i$) und die Druck in Endlage (e) ($p_e$) bei der Positionieren am Ende des Rohres ($L_e$) ausgesetzt wird, entsteht entlang von der Rohrlänge ($\Delta L$) Eine Druckunterschied ($\Delta p_s$), was das Profil von die Geschwindigkeit auf einer Zylinder-Radio ($v$) ergibt:

Bei Str mungen mit niedrigen Werten von der Anzahl der Reynold ($Re$), wo die Viskosit t bedeutender ist als die Tr gheit der Fl ssigkeit, entwickelt sich der Fluss laminar, das hei t ohne das Vorhandensein von Turbulenzen.
(ID 2218)
Im laminaren Fluss bewegen sich benachbarte Schichten, und zwischen ihnen wirkt eine durch die Viskosit t erzeugte Kraft. Die schnellere Schicht zieht ihre langsamere Nachbarschicht mit, w hrend die langsamere Schicht den Fortschritt der schnelleren einschr nkt.
Daher ist die Kraft die Viscose Kraft ($F_v$), die von ERROR:10119.1 ber die andere erzeugt wird, eine Funktion von ERROR:5556.1, ERROR:5436.1 und ERROR:5422.1, wie in der folgenden Gleichung dargestellt:
| $ F_v =- S \eta \displaystyle\frac{ \Delta v }{ \Delta z }$ |
illustriert im folgenden Diagramm:

(ID 7053)
Der laminare Fluss um einen Zylinder kann als mehrere zylindrische Schichten dargestellt werden, die unter dem Einfluss benachbarter Schichten gleiten. In diesem Fall wird die Viscose Kraft ($F_v$) mit der Rohrlänge ($\Delta L$), die Viskosität ($\eta$) und den Variablen die Zylinder-Stern Position ($r$) und die Geschwindigkeit auf einer Zylinder-Radio ($v$) wie folgt ausgedr ckt:
| $ F_v =-2 \pi r \Delta L \eta \displaystyle\frac{ dv }{ dr }$ |
Die Schicht am Rand bei ERROR:5417.1 bleibt aufgrund des Randeffekts stehen und verlangsamt durch die Viskosität ($\eta$) die benachbarte Schicht, die eine Geschwindigkeit hat.
Das Zentrum ist der Teil, der sich mit die Maximale Durchflussrate ($v_{max}$) bewegt und die umgebende Schicht mitzieht. Diese Schicht zieht wiederum die n chste Schicht und so weiter, bis sie die Schicht erreicht, die Kontakt mit der Zylinderwand hat, die sich nicht bewegt.

Auf diese Weise bertr gt das System Energie von der Mitte zur Wand und erzeugt ein Geschwindigkeitsprofil, das wie folgt dargestellt wird:
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
mit:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
(ID 7057)
Das Profil von die Geschwindigkeit auf einer Zylinder-Radio ($v$) in der Positionsradius in einem Rohr ($r$) erm glicht es uns, der Volumenstrom ($J_V$) in einem Rohr durch Integration ber die gesamte Oberfl che zu berechnen, was zur bekannten Hagen-Poiseuille-Gesetz f hrt.

Das Ergebnis ist eine Gleichung, die von ERROR:5417,0 zur vierten Potenz abh ngt. Es ist jedoch entscheidend zu beachten, dass dieses Str mungsprofil nur im Falle einer laminaren Str mung g ltig ist.
Daraus ergibt sich mit die Viskosität ($\eta$), dass der Volumenstrom ($J_V$) vor ein Rohrlänge ($\Delta L$) und eine Variación de la Presión ($\Delta p$) die Ausdruck:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Die Originalarbeiten, die zu diesem Gesetz mit einem kombinierten Namen f hrten, waren:
![]() "Ueber die Gesetze, welche des der Strom des Wassers in r hrenf rmigen Gef ssen bestimmen", Gotthilf Hagen, Annalen der Physik und Chemie 46:423442 (1839).
"Ueber die Gesetze, welche des der Strom des Wassers in r hrenf rmigen Gef ssen bestimmen", Gotthilf Hagen, Annalen der Physik und Chemie 46:423442 (1839).
![]() "Recherches exp rimentales sur le mouvement des liquides dans les tubes de tr s-petits diam tres" (Experimentelle Untersuchungen zur Bewegung von Fl ssigkeiten in R hren mit sehr kleinen Durchmessern), Jean-Louis-Marie Poiseuille, Comptes Rendus de l'Acad mie des Sciences 9:433544 (1840).
"Recherches exp rimentales sur le mouvement des liquides dans les tubes de tr s-petits diam tres" (Experimentelle Untersuchungen zur Bewegung von Fl ssigkeiten in R hren mit sehr kleinen Durchmessern), Jean-Louis-Marie Poiseuille, Comptes Rendus de l'Acad mie des Sciences 9:433544 (1840).
(ID 2216)
W hrend ein Abgelaufene Zeit ($\Delta t$) bewegt sich die Fl ssigkeit mit eine Mittlere Geschwindigkeit der Flüssigkeit ($v$) um ein Rohrelement ($\Delta s$). Wenn die Abschnitt ($S$) die Menge an Fl ssigkeit darstellt, die in der Abgelaufene Zeit ($\Delta t$) diesen Abschnitt durchquert, wird sie wie folgt berechnet:
$\Delta V = S \Delta s = Sv \Delta t$
Diese Gleichung besagt, dass das Volumen der Fl ssigkeit, das w hrend ein Abgelaufene Zeit ($\Delta t$) durch den Abschnitt die Abschnitt ($S$) flie t, gleich dem Produkt aus der Querschnittsfl che und der zur ckgelegten Distanz der Fl ssigkeit in dieser Zeit ist.

Dies erleichtert die Berechnung von der Volumenelement ($\Delta V$), dem Volumen der Fl ssigkeit, das in einem bestimmten Zeitraum von der Abgelaufene Zeit ($\Delta t$) durch den Kanal flie t, entsprechend der Volumenstrom ($J_V$).
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
(ID 2212)
(ID 15221)
Das entscheidende Kriterium zur Bestimmung, ob ein Medium laminar oder turbulent ist, ist die sogenannte Reynolds-Zahl, die die Energie, die mit der Tr gheit verbunden ist, mit derjenigen vergleicht, die mit der Viskosit t verbunden ist. Erstere h ngt von die Dichte ($\rho$), die Mittlere Geschwindigkeit der Flüssigkeit ($v$) und die Typische Abmessungen des Systems ($R$) ab, w hrend letztere von die Viskosität ($\eta$) abh ngt. Sie wird definiert als:
| $ Re =\displaystyle\frac{ \rho R v }{ \eta }$ |
(ID 3177)
Wenn die Druck in der Ausgangsposition ($p_i$) und die Druck in Endlage (e) ($p_e$) miteinander verbunden werden, entsteht eine die Druckunterschied ($\Delta p_s$), die mithilfe der folgenden Formel berechnet wird:
| $ \Delta p = p_e - p_i $ |
die Druckunterschied ($\Delta p_s$) repr sentiert den Druckunterschied, der bewirkt, dass die Fl ssigkeit von der h heren S ule zur niedrigeren S ule str mt.
(ID 14459)
Um den Fluss zu beschreiben, wird ein Koordinatensystem definiert, in dem die Fl ssigkeit von der Position am Anfang des Rohres ($L_i$) nach der Positionieren am Ende des Rohres ($L_e$) flie t, was bedeutet, dass der Druck bei die Druck in der Ausgangsposition ($p_i$) gr er ist als bei die Druck in Endlage (e) ($p_e$). Diese Bewegung h ngt von der Rohrlänge ($\Delta L$) ab, das wie folgt berechnet wird:
| $ \Delta L = L_e - L_i $ |
(ID 3802)
Die Viscose Kraft ($F_v$) kann aus die Parallele Flächen ($S$), die Viskosität ($\eta$), die Geschwindigkeitsunterschied zwischen Oberflächen ($\Delta v$) und die Abstand zwischen Oberflächen ($\Delta z$) mit folgender Methode berechnet werden:
| $ F_v =- S \eta \displaystyle\frac{ \Delta v }{ \Delta z }$ |
(ID 3622)
Im Falle eines Zylinders wird die Oberfl che durch ERROR:5430,0 definiert und durch den Umfang jeder der internen Zylinder, der durch die Multiplikation von $2\pi$ mit der Positionsradius in einem Rohr ($r$) berechnet wird. Damit wird die Zylinderwiderstandskraft ($F_v$) unter Verwendung von die Viskosität ($\eta$) und die Geschwindigkeitsvariation zwischen zwei Radien ($dv$) f r die Breite des Zylinders der Radiusvariation in einem Rohr ($dr$) berechnet, was zu folgendem Ergebnis f hrt:
| $ F_v =-2 \pi r \Delta L \eta \displaystyle\frac{ dv }{ dr }$ |
(ID 3623)
Beim L sen der Flie gleichung mit der Randbedingung erhalten wir die Geschwindigkeit auf einer Zylinder-Radio ($v$) als Funktion von der Krümmung Radio ($r$), dargestellt als Parabel mit dem Mittelpunkt bei die Maximale Durchflussrate ($v_{max}$) und Nullwert bei der Rohrradius ($R$):
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
.
(ID 3627)
Der Wert von die Maximale Durchflussrate ($v_{max}$) in der Mitte eines Zylinders h ngt von die Viskosität ($\eta$), der Rohrradius ($R$) und dem Gradienten ab, der von die Druckunterschied ($\Delta p_s$) und der Rohrlänge ($\Delta L$) erzeugt wird, wie unten dargestellt:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
Das negative Vorzeichen deutet darauf hin, dass der Fluss immer in entgegengesetzter Richtung zum Gradienten erfolgt, d.h., von der Region mit h herem Druck zur Region mit niedrigerem Druck.
(ID 3628)
Der Volumenstrom ($J_V$) entspricht der Menge von ERROR:9847,0, die w hrend ein Zeit ($t$) durch den Kanal flie t. Daher haben wir:
| $ J_V =\displaystyle\frac{ dV }{ dt }$ |
(ID 12713)
Der Volumenstrom ($J_V$) l sst sich mit dem Hagen-Poiseuille-Gesetz berechnen, das mit den Parametern die Viskosität ($\eta$), die Druckunterschied ($\Delta p$), der Rohrradius ($R$) und der Rohrlänge ($\Delta L$) lautet:
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
(ID 3178)
Mit der Rohrradius ($R$), die Viskosität ($\eta$) und der Rohrlänge ($\Delta L$) haben wir, dass eine Hydraulische Leitfähigkeit ($G_h$) ist:
| $ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$ |
(ID 15102)
Durch die Einf hrung von die Hydraulische Leitfähigkeit ($G_h$) k nnen wir die Hagen-Poiseuille-Gleichung mit die Druckunterschied ($\Delta p$) und der Volumenstrom ($J_V$) mithilfe der folgenden Gleichung umschreiben:
| $ J_V = G_h \Delta p $ |
(ID 14471)
Im Zusammenhang mit dem elektrischen Widerstand gibt es dessen Inverses, das als elektrische Leitf higkeit bekannt ist. Ebenso kann das, was die Hydraulische Leitfähigkeit ($G_h$) w re, in Bezug auf die Hydraulic Resistance ($R_h$) durch den Ausdruck definiert werden:
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
(ID 15092)
Da die Hydraulic Resistance ($R_h$) dem Kehrwert von die Hydraulische Leitfähigkeit ($G_h$) entspricht, kann es aus dem Ausdruck des letzteren berechnet werden. Auf diese Weise k nnen wir Parameter identifizieren, die mit der Geometrie (der Rohrlänge ($\Delta L$) und der Rohrradius ($R$)) und der Art des Fluids (die Viskosität ($\eta$)) zusammenh ngen und die gemeinsam als eine Hydraulic Resistance ($R_h$) bezeichnet werden k nnen:
| $ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$ |
(ID 3629)
Darcy schreibt die Hagen-Poiseuille-Gleichung so um, dass die Druckunterschied ($\Delta p$) gleich die Hydraulic Resistance ($R_h$) mal der Volumenstrom ($J_V$) ist:
| $ \Delta p = R_h J_V $ |
(ID 3179)
Die Oberfläche einer Scheibe ($S$) von ein Scheibenradius ($r$) wird wie folgt berechnet:
| $ S = \pi r ^2$ |
(ID 3804)
Eine Flussdichte ($j_s$) kann in Bezug auf der Volumenstrom ($J_V$) durch die Abschnitt oder Bereich ($S$) mit der folgenden Formel dargestellt werden:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
(ID 4349)
Der verbleibende Faktor wird die Hydrodynamische Permeabilität ($k$) genannt und kann mit der Rohrradius ($R$) nach folgender Formel berechnet werden:
| $ k = \displaystyle\frac{ R ^2}{8}$ |
(ID 108)
ID:(369, 0)
