Bodenströmung
Storyboard 
Im Falle von Boden kann angenommen werden, dass er mehrere Poren enthält, die kleine Kapillaren bilden, die ihn durchziehen. Auf dieser Grundlage können die Gleichungen für laminaren Fluss durch Röhren angewendet und die hydraulischen Widerstände von Kapillarnetzwerken berechnet werden. Diese Widerstände hängen von der Porosität ab und somit von dem Verhältnis der verschiedenen Bestandteile.
ID:(370, 0)
Durch den Boden fließen
Konzept 
Die einzelnen Poren kommen zusammen und bilden Ketten, die Kapillaren erzeugen, durch die Wasser fließt.
Um dieses Phänomen zu modellieren, ist es notwendig, sowohl den Radius dieser Kapillaren als auch ihre Länge zu schätzen, wobei zu beachten ist, dass sie in der Regel nicht gerade verlaufen.
ID:(937, 0)
Abschnitt der Probenporen
Konzept 
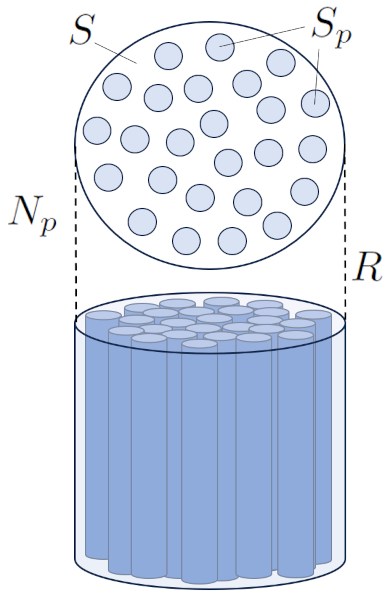
Die Abschnitt Fluss ($S$) beinhaltet das von der Anzahl der Kapillaren ($N_p$) erzeugte die Porenabschnitt ($S_p$):
None
ID:(2285, 0)
Zusammenhang zwischen Anzahl der Körner und Poren
Konzept 
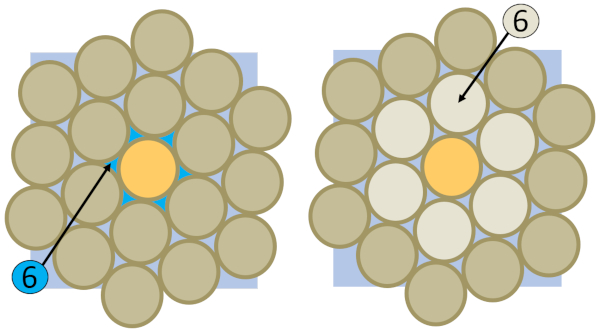
Wenn wir einen Querschnitt des Bodens betrachten, werden wir feststellen, dass die Kapillaren durch die Zwischenräume zwischen den Körnern verlaufen. Dadurch ist ihre Anzahl ähnlich der Anzahl der Körner selbst, sodass wir annehmen können, dass der Anzahl der Kapillaren ($N_p$) ähnlich der Anzahl der Körner in diesem Querschnitt ist:
None
ID:(2283, 0)
Fließen durch einzelne Poren
Konzept 
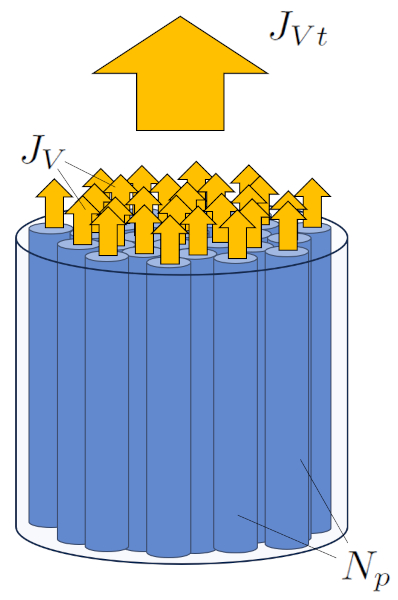
Der Gesamtfluss wird als Summe der einzelnen Strömungen durch die verschiedenen Poren berechnet:
None
Wenn wir annehmen, dass alle Poren identisch sind, können wir der Gesamtfluss ($J_{Vt}$) erhalten, indem wir der Volumenstrom ($J_V$) einzeln mit der Anzahl der Kapillaren ($N_p$) multiplizieren.
ID:(2286, 0)
Hydraulische Leitfähigkeit für verschiedene Böden
Bild 
Wenn wir die Literatur betrachten, finden wir Schätzungen der hydraulischen Leitfähigkeit für verschiedene Bodentexturen, die hier in Abhängigkeit von ihrem Exponenten dargestellt sind (d.h., -7 wird für eine hydraulische Leitfähigkeit von 1E-7 m/s angegeben):
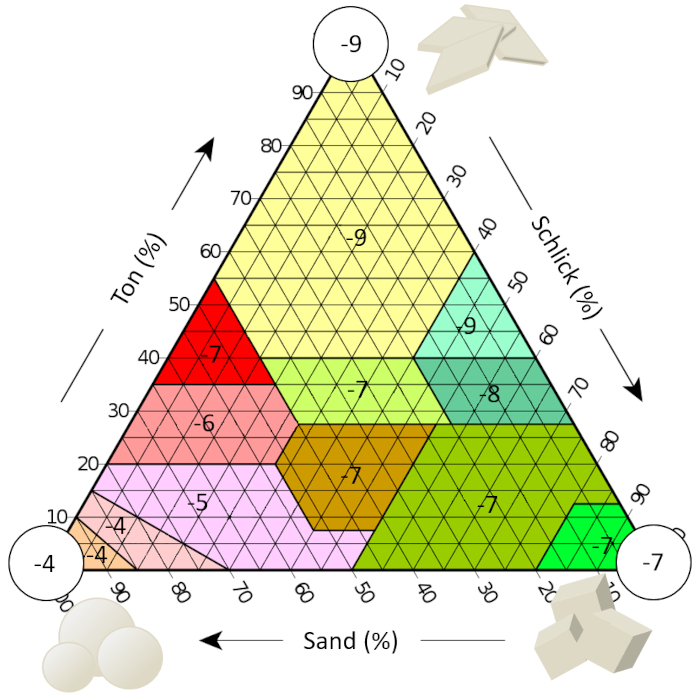
Die Ergebnisse sind in der folgenden Tabelle zusammengefasst:
| Textur | $g_a$ [%] | $g_i$ [%] | $g_c$ [%] | $f$ [%] | $K$ [m/s] |
| Ton | 0-45 | 0-40 | 55-100 | 40-50 | 1E-9 - 1E-8 [1] |
| Lehm | 23-52 | 28-50 | 8-27 | 40-50 | 1E-7 - 1E-5 [2] |
| Sand | 85-100 | 0-15 | 0-10 | 25-35 | 1E-4 - 1E-2 [3] |
| Schluff | 0-20 | 80-100 | 0-13 | 35-45 | 1E-7 - 1E-5 [4] |
| Schluffiger Ton | 0-20 | 40-60 | 40-60 | 40-50 | 1E-9 - 1E-8 [1] |
| Sandiger Ton | 45-65 | 0-20 | 35-55 | 35-45 | 1E-7 - 1E-5 [5] |
| Sandiger Lehm | 20-45 | 15-53 | 28-40 | 40-50 | 1E-7 - 1E-5 [2] |
| Lehmiger Schluff | 0-20 | 40-73 | 28-40 | 40-50 | 1E-8 - 1E-6 [6] |
| Sandiger lehmiger Lehm | 45-80 | 0-33 | 20-35 | 35-45 | 1E-6 - 1E-4 [1] |
| Schluffiger Lehm | 0-50 | 50-88 | 0-28 | 35-45 | 1E-7 - 1E-5 [4] |
| Sandiger Schluff | 43-85 | 0-50 | 0-20 | 30-40 | 1E-5 - 1E-3 [2] |
| Sandiger schluffiger Lehm | 70-90 | 0-30 | 0-15 | 25-35 | 1E-4 - 1E-2 [4] |
Diese Daten wurden aus der folgenden Literatur entnommen, die in der Spalte "hydraulische Leitfähigkeit" referenziert ist:[1] "Geotechnical Engineering Principles and Practices" von Donald P. Coduto et al., Prentice Hall (1999)[2] "Soil Mechanics and Foundations" von Muni Budhu, John Wiley & Sons. (2011)[3] "Introduction to Environmental Engineering" von Mackenzie Davis und David Cornwell, McGraw Hill (2022)[4] "Principles of Geotechnical Engineering" von Braja M. Das, CL-Engineering (2009)[5] "Soil Mechanics in Engineering Practice" von Karl Terzaghi und Ralph B. Peck, John Wiley & Sons. (1996)[6] "Soil Mechanics: Concepts and Applications" von William Powrie, CRC Press (2013)
ID:(4740, 0)
Bodenströmung
Modell 
Im Falle von Boden kann angenommen werden, dass er mehrere Poren enthält, die kleine Kapillaren bilden, die ihn durchziehen. Auf dieser Grundlage können die Gleichungen für laminaren Fluss durch Röhren angewendet und die hydraulischen Widerstände von Kapillarnetzwerken berechnet werden. Diese Widerstände hängen von der Porosität ab und somit von dem Verhältnis der verschiedenen Bestandteile.
Variablen
Berechnungen
Berechnungen
Gleichungen
Wenn wir den Bereich im Querschnitt betrachten, der keine Poren enth lt, indem wir die Porenabschnitt ($S_p$) von die Abschnitt Fluss ($S$) subtrahieren und ihn durch den Bereich eines generischen Korns mit einem Radius von ERROR:10129,0 teilen, erhalten wir die Anzahl der sichtbaren K rner im Schnitt:
$\displaystyle\frac{S-S_p}{\pi r_0^2}=\displaystyle\frac{(1-f)S}{\pi r_0^2}$
wobei wir die Beziehung f r die Porosität ($f$) verwenden:
| $ f = \displaystyle\frac{ S_p }{ S }$ |
Wenn die Anzahl der K rner mit ERROR:6039,0 gem dem Ausdruck ist:
| $ N_p =\displaystyle\frac{ f S }{ \pi R ^2}$ |
wobei der Radius der Rohrradius ($R$) ist. Damit erhalten wir die Beziehung:
$\displaystyle\frac{(1-f)S}{\pi r_0^2}=\displaystyle\frac{fS}{\pi R^2}$
was zu folgendem Ergebnis f hrt:
| $ R = \sqrt{\displaystyle\frac{ f }{1- f }} r_0 $ |
(ID 109)
Mit der H he die Infinitesimale Entfernung ($ds$) ist das Volumen von die Abschnitt Fluss ($S$)
$S ds$
und das der Poren mit die Porenabschnitt ($S_p$)
$S_p ds$
Daher wird die Porosität ($f$) wie folgt berechnet:
$f = \displaystyle\frac{S_p ds}{S ds} = \displaystyle\frac{S_p}{S}$
resultierend in folgender Gleichung:
| $ f = \displaystyle\frac{ S_p }{ S }$ |
(ID 938)
Das Volumen des Kapillars kann aus der Rohrradius ($R$) und die Kapillarlänge ($l$) berechnet werden, was gleich dem Volumen einer Kette von K rnern von der Radius einer generischen Korns ($r_0$) und der Rohrlänge ($\Delta L$) multipliziert mit die Generische eigene Porosität ($q_0$) ist:
$\pi R^2 l = q_0 \pi r_0^2 \Delta L$
Dies in Verbindung mit die Porosität ($f$) in der Beziehung
| $ R = \sqrt{\displaystyle\frac{ f }{1- f }} r_0 $ |
ergibt die folgende Beziehung:
| $ l = q_0 \displaystyle\frac{(1- f )}{ f } \Delta L $ |
(ID 2215)
Wie die Porosität ($f$), berechnet mit die Porenabschnitt ($S_p$) und die Abschnitt Fluss ($S$) unter Verwendung von
| $ f = \displaystyle\frac{ S_p }{ S }$ |
zusammen mit der Gleichung zur Berechnung von die Porenabschnitt ($S_p$) basierend auf der Anzahl der Kapillaren ($N_p$) und der Rohrradius ($R$) durch
| $ S_p = N_p \pi R ^2$ |
ergibt sich
$f = \displaystyle\frac{N_p\pi R^2}{S}$
kann f r der Anzahl der Kapillaren ($N_p$) gel st werden und ergibt
| $ N_p =\displaystyle\frac{ f S }{ \pi R ^2}$ |
(ID 4363)
Um der Gesamtfluss ($J_{Vt}$) unter Verwendung von der Anzahl der Kapillaren ($N_p$) und der Volumenstrom ($J_V$) f r jeden Kapillar durch
| $ J_{Vt} = N_p J_V $ |
zu berechnen, erhalten wir der Anzahl der Kapillaren ($N_p$) mit die Porosität ($f$), die Abschnitt Fluss ($S$) und der Rohrradius ($R$) durch
| $ N_p =\displaystyle\frac{ f S }{ \pi R ^2}$ |
und das Hagen-Poiseuille-Gesetz unter Verwendung von die Viskosität ($\eta$), die Druckunterschied ($\Delta p$) und die Kapillarlänge ($l$) wird berechnet mit
$J_v = - \displaystyle\frac{\pi R^4}{8\eta}\displaystyle\frac{\Delta p}{l}$
Unter Verwendung der Beziehung f r der Rohrradius ($R$) in Bezug auf der Radius einer generischen Korns ($r_0$)
| $ R = \sqrt{\displaystyle\frac{ f }{1- f }} r_0 $ |
und f r die Kapillarlänge ($l$), die Generische eigene Porosität ($q_0$) und der Probenlänge ($\Delta L$)
| $ l = q_0 \displaystyle\frac{(1- f )}{ f } \Delta L $ |
erhalten wir
| $ J_{Vt} =-\displaystyle\frac{ r_0 ^2}{8 \eta q_0 }\displaystyle\frac{ f ^3}{(1- f )^2}\displaystyle\frac{ S }{ \Delta L } \Delta p $ |
(ID 4365)
Im Fall von Kapillaren, durch die eine Fl ssigkeit mit die Flüssigkeitsdichte ($\rho_w$) aufgrund von die Druckunterschied ($\Delta p$), erzeugt durch eine Höhendifferenz ($\Delta h$) unter dem Einfluss der Schwerkraft, dargestellt durch die Gravitationsbeschleunigung ($g$), flie t und mit der folgenden Gleichung berechnet wird:
| $ \Delta p = \rho_w g \Delta h $ |
kann dies in die Hagen-Poiseuille-Gleichung einbezogen werden, bezogen auf der Gesamtfluss ($J_{Vt}$), die wiederum von der Radius einer generischen Korns ($r_0$), die Generische eigene Porosität ($q_0$), die Porosität ($f$), die Viskosität ($\eta$), die Abschnitt oder Bereich ($S$) und der Probenlänge ($\Delta L$) abh ngt, wie in der Gleichung beschrieben:
| $ J_{Vt} =-\displaystyle\frac{ r_0 ^2}{8 \eta q_0 }\displaystyle\frac{ f ^3}{(1- f )^2}\displaystyle\frac{ S }{ \Delta L } \Delta p $ |
Zusammen mit der Definition von die Flussdichte ($j_s$):
$j_s = \displaystyle\frac{J_{Vt}}{S}$
Erhalten wir:
$j_s=\displaystyle\frac{J_{Vt}}{S}=\displaystyle\frac{ r_0 ^2 }{8 q_g }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }\displaystyle\frac{ \Delta h }{ L }$
resultierend in:
| $ j_s =-\displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }\displaystyle\frac{ \Delta h }{ \Delta L }$ |
(ID 4366)
Da die Flussdichte ($j_s$) durch die Gleichung:
| $ j_s =-\displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }\displaystyle\frac{ \Delta h }{ \Delta L }$ |
mit der Radius einer generischen Korns ($r_0$), die Porosität ($f$), die Flüssigkeitsdichte ($\rho_w$), die Gravitationsbeschleunigung ($g$), die Viskosität ($\eta$), die Generische eigene Porosität ($q_0$), die Höhendifferenz ($\Delta h$) und der Probenlänge ($\Delta L$) in Beziehung steht, k nnen wir einen Faktor definieren, den wir die Hydraulische Leitfähigkeit ($K_s$) nennen, wie folgt:
| $ K_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }$ |
Dieser Faktor umfasst alle Elemente, die mit den Eigenschaften des Bodens und der Fl ssigkeit, die durch ihn flie t, zusammenh ngen.
(ID 4739)
Mit Darcys Gesetz, wo die Druckunterschied ($\Delta p$) gleich die Hydraulic Resistance ($R_h$) ist und der Gesamtfluss ($J_{Vt}$):
| $ \Delta p = R_h J_V $ |
Daher ergibt sich mit der Gleichung f r den Boden mit die Abschnitt Fluss ($S$), der Radius einer generischen Korns ($r_0$), die Viskosität ($\eta$), die Generische eigene Porosität ($q_0$), die Porosität ($f$), die Druckunterschied ($\Delta p$) und der Probenlänge ($\Delta L$):
| $ J_{Vt} =-\displaystyle\frac{ r_0 ^2}{8 \eta q_0 }\displaystyle\frac{ f ^3}{(1- f )^2}\displaystyle\frac{ S }{ \Delta L } \Delta p $ |
Deshalb ist die Hydraulic Resistance ($R_h$):
| $ R_h = \displaystyle\frac{8 \eta q_0 }{ r_0 ^2}\displaystyle\frac{(1- f )^2 }{f ^3}\displaystyle\frac{ \Delta L }{ S }$ |
(ID 10594)
Beispiele
(ID 15203)
Die einzelnen Poren kommen zusammen und bilden Ketten, die Kapillaren erzeugen, durch die Wasser flie t.
Um dieses Ph nomen zu modellieren, ist es notwendig, sowohl den Radius dieser Kapillaren als auch ihre L nge zu sch tzen, wobei zu beachten ist, dass sie in der Regel nicht gerade verlaufen.
(ID 937)
(ID 2284)
Die Abschnitt Fluss ($S$) beinhaltet das von der Anzahl der Kapillaren ($N_p$) erzeugte die Porenabschnitt ($S_p$):

None
(ID 2285)
Wenn wir einen Querschnitt des Bodens betrachten, werden wir feststellen, dass die Kapillaren durch die Zwischenr ume zwischen den K rnern verlaufen. Dadurch ist ihre Anzahl hnlich der Anzahl der K rner selbst, sodass wir annehmen k nnen, dass der Anzahl der Kapillaren ($N_p$) hnlich der Anzahl der K rner in diesem Querschnitt ist:

None
(ID 2283)
(ID 2291)
Der Gesamtfluss wird als Summe der einzelnen Str mungen durch die verschiedenen Poren berechnet:

None
Wenn wir annehmen, dass alle Poren identisch sind, k nnen wir der Gesamtfluss ($J_{Vt}$) erhalten, indem wir der Volumenstrom ($J_V$) einzeln mit der Anzahl der Kapillaren ($N_p$) multiplizieren.
(ID 2286)
Wenn wir die Literatur betrachten, finden wir Sch tzungen der hydraulischen Leitf higkeit f r verschiedene Bodentexturen, die hier in Abh ngigkeit von ihrem Exponenten dargestellt sind (d.h., -7 wird f r eine hydraulische Leitf higkeit von 1E-7 m/s angegeben):

Die Ergebnisse sind in der folgenden Tabelle zusammengefasst:
| Textur | $g_a$ [%] | $g_i$ [%] | $g_c$ [%] | $f$ [%] | $K$ [m/s] |
| Ton | 0-45 | 0-40 | 55-100 | 40-50 | 1E-9 - 1E-8 [1] |
| Lehm | 23-52 | 28-50 | 8-27 | 40-50 | 1E-7 - 1E-5 [2] |
| Sand | 85-100 | 0-15 | 0-10 | 25-35 | 1E-4 - 1E-2 [3] |
| Schluff | 0-20 | 80-100 | 0-13 | 35-45 | 1E-7 - 1E-5 [4] |
| Schluffiger Ton | 0-20 | 40-60 | 40-60 | 40-50 | 1E-9 - 1E-8 [1] |
| Sandiger Ton | 45-65 | 0-20 | 35-55 | 35-45 | 1E-7 - 1E-5 [5] |
| Sandiger Lehm | 20-45 | 15-53 | 28-40 | 40-50 | 1E-7 - 1E-5 [2] |
| Lehmiger Schluff | 0-20 | 40-73 | 28-40 | 40-50 | 1E-8 - 1E-6 [6] |
| Sandiger lehmiger Lehm | 45-80 | 0-33 | 20-35 | 35-45 | 1E-6 - 1E-4 [1] |
| Schluffiger Lehm | 0-50 | 50-88 | 0-28 | 35-45 | 1E-7 - 1E-5 [4] |
| Sandiger Schluff | 43-85 | 0-50 | 0-20 | 30-40 | 1E-5 - 1E-3 [2] |
| Sandiger schluffiger Lehm | 70-90 | 0-30 | 0-15 | 25-35 | 1E-4 - 1E-2 [4] |
Diese Daten wurden aus der folgenden Literatur entnommen, die in der Spalte "hydraulische Leitf higkeit" referenziert ist:[1] "Geotechnical Engineering Principles and Practices" von Donald P. Coduto et al., Prentice Hall (1999)[2] "Soil Mechanics and Foundations" von Muni Budhu, John Wiley & Sons. (2011)[3] "Introduction to Environmental Engineering" von Mackenzie Davis und David Cornwell, McGraw Hill (2022)[4] "Principles of Geotechnical Engineering" von Braja M. Das, CL-Engineering (2009)[5] "Soil Mechanics in Engineering Practice" von Karl Terzaghi und Ralph B. Peck, John Wiley & Sons. (1996)[6] "Soil Mechanics: Concepts and Applications" von William Powrie, CRC Press (2013)
(ID 4740)
(ID 15222)
ID:(370, 0)
