Densidade de fluxo e condutividade hidráulica
Conceito 
La densidade de fluxo ($j_s$) pode ser expresso em termos de la condutividade hidráulica ($K_s$), no limite infinitesimal com la diferencial de altura da coluna ($dh$) e la diferencial de distância ($dx$), da seguinte forma:
| $ j_s = - K_s \displaystyle\frac{ dh }{ dx }$ |
Isso significa que quanto mais íngreme for o gradiente ou quanto mais íngreme for o terreno, maior será o valor de la densidade de fluxo ($j_s$), como ilustrado no gráfico:
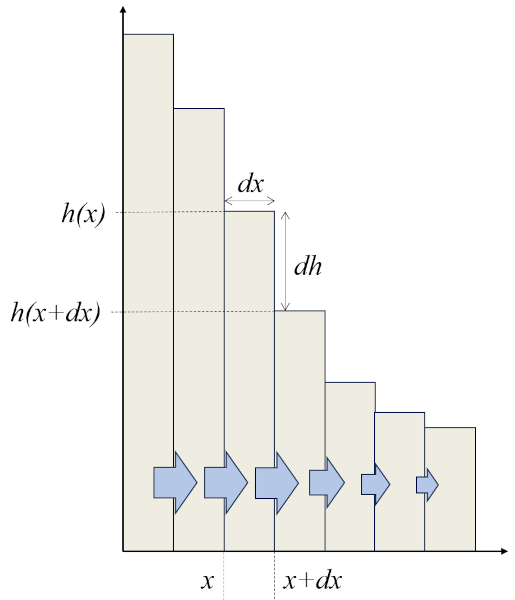
O gráfico mostra como as barras com valores iguais de ERROR:10142,0 têm valores progressivamente menores de ERROR:10141,0, resultando em um valor decrescente de ERROR:7220,0. Como o volume do líquido é conservado, isso só é possível se houver outro fluxo que compense essa redução em ERROR:7220,0. Isso poderia ser um fluxo perpendicular ao mostrado no gráfico, por exemplo, se as barras mais curtas forem mais largas em uma direção perpendicular ao gráfico.
Este problema leva às seguintes considerações:
A altura $h$ do líquido só pode ser calculada como resultado da solução de uma equação diferencial, uma vez que deve satisfazer a exigência de que o volume seja conservado em toda a área onde ocorre o fluxo.
Além disso, é importante ter em mente que:
O sinal negativo reflete o fato de que o fluxo sempre ocorre da zona de maior altitude para a zona de menor altitude. Se a inclinação for negativa, o sinal negativo resulta em um fluxo positivo (da esquerda para a direita), e, inversamente, se a inclinação for positiva, o fluxo é negativo (da direita para a esquerda).
ID:(930, 0)
Equação de fluxo em uma dimensão
Conceito 
Se estudarmos o caso unidimensional, descrevendo o processo ao longo do eixo $x$, podemos observar como a altura da coluna $\Delta h$ varia durante um intervalo de tempo $\Delta t$. Neste caso, uma coluna com largura $\Delta x$ mudará seu volume por unidade de comprimento ao longo do tempo como $\Delta x \Delta h/\Delta t$. Por outro lado, a quantidade de líquido que entra ao longo da coluna em $x$ é $h(x) j_s(x)$, enquanto em $x+\Delta x$ sai como $h(x+\Delta x) j_s(x+\Delta x)$:
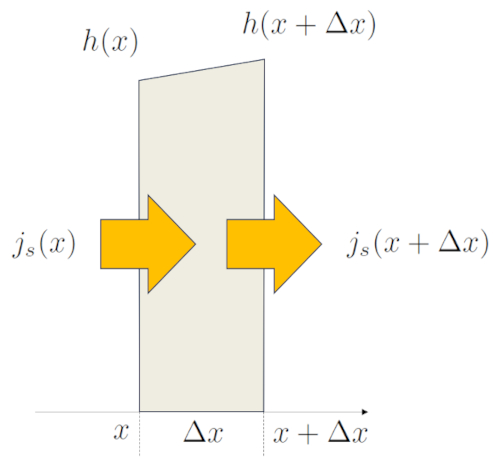
Portanto, a variação de la altura da coluna d'água no solo ($h$) ao longo do tempo é igual à variação do produto de la altura da coluna d'água no solo ($h$) e la densidade de fluxo ($j_s$) na posição:
| $\displaystyle\frac{\partial h}{\partial t} = - \displaystyle\frac{\partial}{\partial x}( h j_s )$ |
As derivadas parciais são semelhantes às derivadas ordinárias, com a diferença de que são aplicadas a funções que dependem de mais de uma variável. Nesses casos, a derivada parcial, representada pelo símbolo $\partial$, lembra a derivada comum representada pela letra $d$, mas com a particularidade de que as variáveis não mencionadas no denominador são mantidas constantes.
ID:(2290, 0)
Fluir para um canal
Conceito 
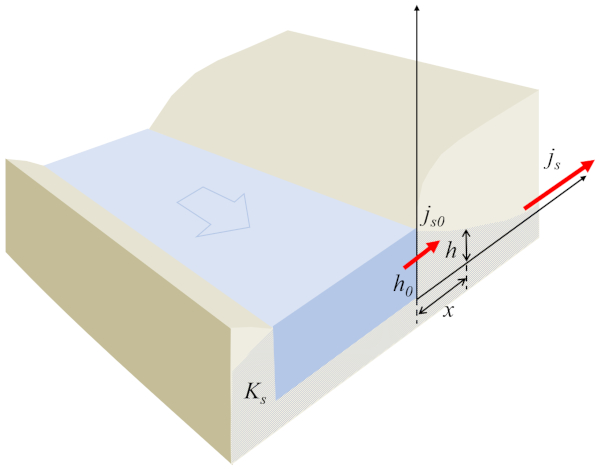
No caso do fluxo em direção a um canal, o sistema pode ser modelado de forma unidimensional, onde la altura da coluna d'água no solo ($h$) é uma função de la posição da coluna d'água no solo ($x$) que representa la densidade de fluxo ($j_s$) e satisfaz a condição
| $ h j_s = h_0 j_{s0} $ |
com o fluxo em um ponto de referência ($j_{s0}$) e la altura de referência da coluna de água ($h_0$) definindo o perfil da água no solo:
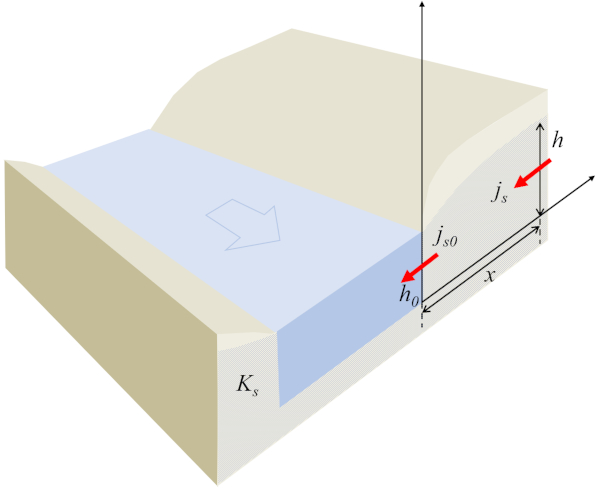
A chave dessa equação é que o produto de la altura da coluna d'água no solo ($h$) e la densidade de fluxo ($j_s$) deve ser sempre constante. Nesse sentido, se la altura da coluna d'água no solo ($h$) aumenta, la densidade de fluxo ($j_s$) diminui e vice-versa. Além disso, o sinal permanece o mesmo; portanto, o fluxo em direção ao canal, ou seja, o fluxo negativo, ocorrerá apenas quando o nível do lençol freático estiver mais alto do que o do canal. À medida que o líquido se aproxima do canal, o nível do lençol freático diminui, levando a um aumento na densidade do fluxo.
ID:(15104, 0)
Solução de altura de fluxo em direção a um canal
Conceito 
A solução para a equação de fluxo unidimensional em direção a um canal, onde la altura da coluna d'água no solo ($h$) é calculado como função de la altura de referência da coluna de água ($h_0$) e la posição da coluna d'água no solo ($x$) na borda do canal, juntamente com o comprimento característico do fluxo no solo ($s_0$), assume a seguinte forma:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \displaystyle\frac{ 2 x }{ s_0 }} $ |
Esta solução é representada graficamente em termos dos fatores adicionais $h/h_0$ e $x/s_0$ da seguinte forma:
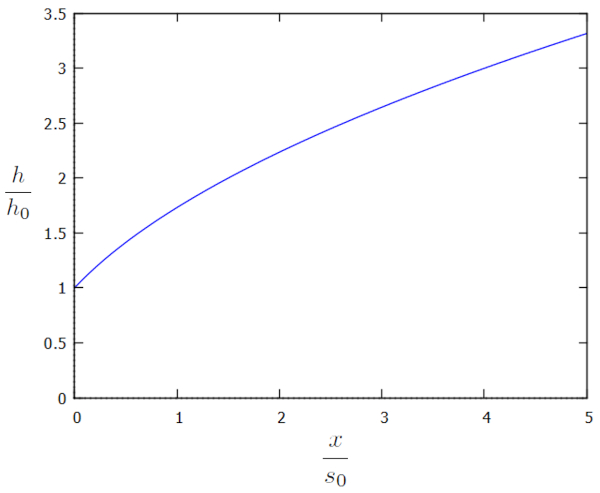
O perfil revela que, longe do canal, a altura da coluna de água é significativamente alta. No entanto, devido à extração de água pelo canal, essa altura começa a diminuir até alcançar a borda do canal. Dinamicamente, la densidade de fluxo ($j_s$) determina a quantidade de água que flui para o canal, enquanto la altura de referência da coluna de água ($h_0$) se ajusta gradualmente até atingir um estado de equilíbrio. Em outras palavras, se o valor de la altura de referência da coluna de água ($h_0$) for muito baixo em relação à quantidade total de água que chega ao canal, ele aumenta; e se for muito alto, diminui. Dessa forma, la altura de referência da coluna de água ($h_0$) adquire o valor que equilibra a quantidade de água que entra com a quantidade de água que flui pelo canal.
ID:(15109, 0)
Solução de densidade de fluxo em direção a um canal
Conceito 
A solução obtida para a altura e os parâmetros o fluxo em um ponto de referência ($j_{s0}$) e la altura de referência da coluna de água ($h_0$) revela que la densidade de fluxo ($j_s$) é dado por:
| $ \displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{1}{\sqrt{1 + \displaystyle\frac{ 2 x }{ s_0 }}} $ |
Podemos representar graficamente la densidade de fluxo ($j_s$) em função dos fatores adicionais $j_s/j_{s0}$ e $x/s_0$ da seguinte maneira:
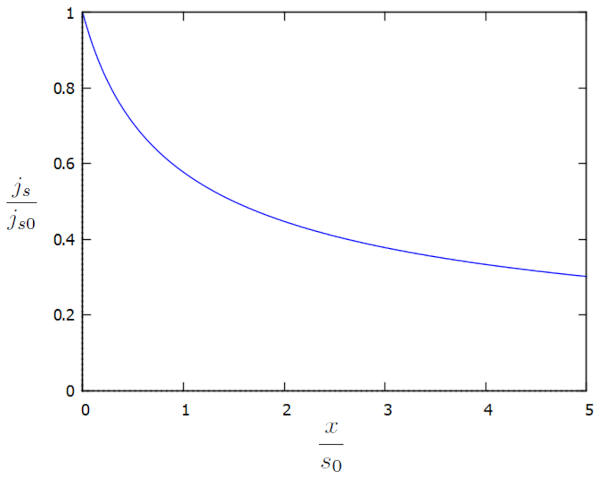
É perceptível que la densidade de fluxo ($j_s$) continua a aumentar à medida que nos aproximamos do canal, à medida que la altura da coluna d'água no solo ($h$) diminui. Esse aumento é necessário para manter a velocidade do fluxo em la densidade de fluxo ($j_s$) ou, alternativamente, para aumentá-la.
ID:(15110, 0)
Fluxo de um canal
Conceito 
No caso em que o fluxo emerge do canal, ocorre uma situação em que o nível de la altura da coluna d'água no solo ($h$) deve diminuir à medida que nos afastamos do canal, garantindo a existência do gradiente de pressão que impulsiona o fluxo. O problema é que, se o fluxo se move rapidamente dentro do meio, a altura tenderá a zero e, como resultado, o fluxo se aproximará do infinito, o que não faz sentido.
Isso significa que não existe uma solução estacionária nesse cenário e a única solução é para o meio se encher até atingir a altura do canal, efetivamente tornando-se constante.
A questão é se existe uma situação estacionária não trivial que represente um cenário real e interessante. Um caso possível é quando o nível do meio diminui a ponto de ficar mais baixo do que a coluna antes que a solução diverja. Esse caso corresponde à situação em que o fluxo emerge na superfície e não há divergência na solução. Isso implicaria que um fluxo é gerado e sai para o exterior em um ponto específico, com o risco de enfraquecer a fundação e, assim, desestabilizar o meio, que age como uma represa.
ID:(4746, 0)
Situação que atende às condições limite
Conceito 
Se considerarmos uma situação em que o fluxo do canal pode emergir na superfície, temos um cenário em que o fluxo entra e depois sai do meio, tornando a solução viável.
A emergência na superfície simplesmente implica que a altura da coluna de líquido se torna maior do que a do meio circundante. Na verdade, semelhante ao caso do fluxo em direção a um canal, isso geraria água na superfície, que, se não for permitida a escoar, realmente formaria um novo canal.
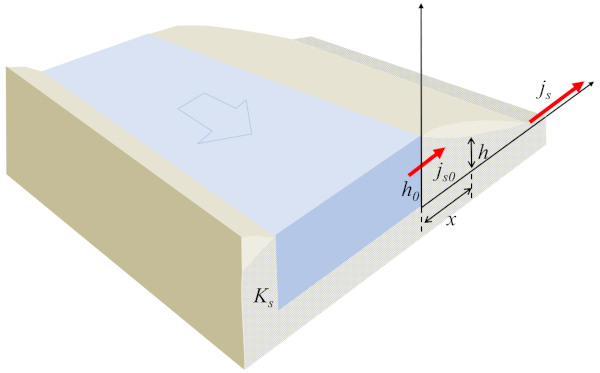
No caso do fluxo saindo de um canal, é possível modelar o sistema de forma unidimensional, onde la altura da coluna d'água no solo ($h$) é uma função de la posição da coluna d'água no solo ($x$) que representa la densidade de fluxo ($j_s$) e satisfaz a seguinte condição:
| $ h j_s = h_0 j_{s0} $ |
Com o fluxo em um ponto de referência ($j_{s0}$) e la altura de referência da coluna de água ($h_0$) definindo o perfil da água no solo, como mostrado na imagem a seguir:

A chave da equação está no fato de que o produto de la altura da coluna d'água no solo ($h$) e la densidade de fluxo ($j_s$) deve permanecer constante o tempo todo. Nesse sentido, se la altura da coluna d'água no solo ($h$) aumentar, la densidade de fluxo ($j_s$) diminuirá e vice-versa. Além disso, o sinal permanece o mesmo. Portanto, o fluxo do canal, ou seja, o fluxo positivo, ocorrerá apenas se a altura do canal for maior do que a do ponto onde o fluxo emerge. À medida que o líquido se afasta do canal, a altura diminuirá e a densidade do fluxo aumentará.
ID:(4370, 0)
Solução de altura de fluxo de um canal
Conceito 
A solução da equação de fluxo unidimensional a partir de um canal, na qual o valor de la altura da coluna d'água no solo ($h$) é calculado em função de la altura de referência da coluna de água ($h_0$) e la posição da coluna d'água no solo ($x$) na borda do canal, juntamente com o comprimento característico do fluxo no solo ($s_0$), assume a seguinte forma:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 - \displaystyle\frac{ 2 x }{ s_0 }} $ |
Essa solução é representada graficamente em termos dos fatores adicionais $h/h_0$ e $x/x_0$ da seguinte maneira:
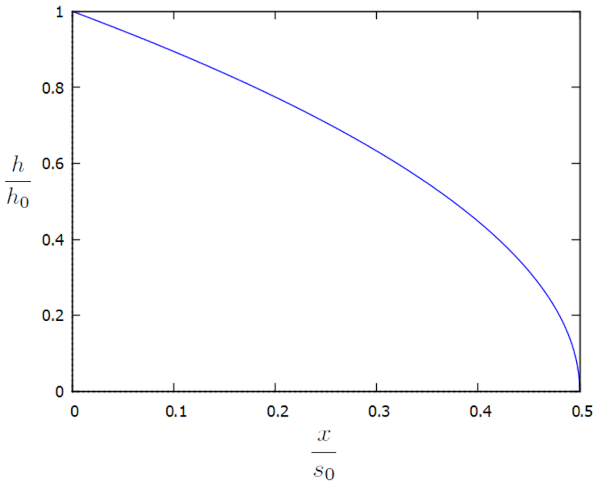
O perfil revela que a altura diminui à medida que nos afastamos do canal para manter um gradiente de pressão. No entanto, surge um problema quando a distância atinge a metade de o comprimento característico do fluxo no solo ($s_0$), pois a altura da coluna chega a zero e não há solução para distâncias maiores (o argumento da raiz quadrada se torna negativo). Em outras palavras, para que a solução faça sentido, deve haver um mecanismo que remova o líquido antes de atingir essa distância crítica.
ID:(4374, 0)
Solução de densidade de fluxo de um canal
Conceito 
A solução obtida para a altura e os parâmetros o fluxo em um ponto de referência ($j_{s0}$) e la altura de referência da coluna de água ($h_0$) nos mostra que la densidade de fluxo ($j_s$) é igual a:
| $ \displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{1}{\sqrt{1 - \displaystyle\frac{ 2 x }{ s_0 }}} $ |
Podemos representar la densidade de fluxo ($j_s$) graficamente em termos dos fatores adicionais $j_s/j_{s0}$ e $x/x_0$ da seguinte maneira:
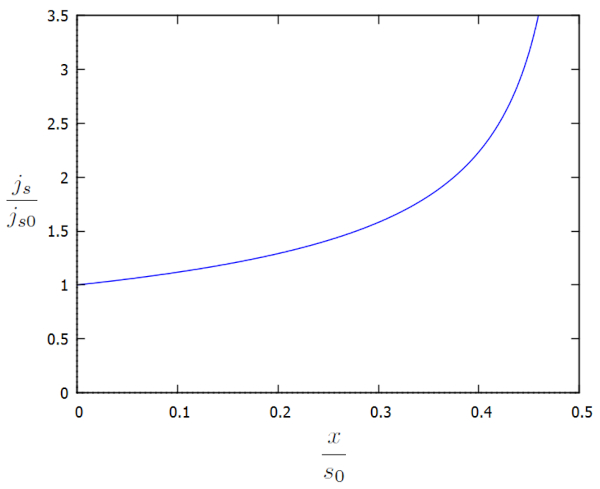
la densidade de fluxo ($j_s$) continua aumentando à medida que nos aproximamos do canal, à medida que la altura da coluna d'água no solo ($h$) diminui. Esse aumento é necessário para manter a velocidade do fluxo em la densidade de fluxo ($j_s$) ou, alternativamente, aumentá-la.
ID:(7827, 0)
Barragem I - Mina Córrego do Feijão
Conceito 
Um exemplo que ilustra o efeito do fluxo através da base no caso de uma barragem ocorreu na Barragem 1 da mina 'Córrego do Feijão' em Brumadinho, Minas Gerais, Brasil.
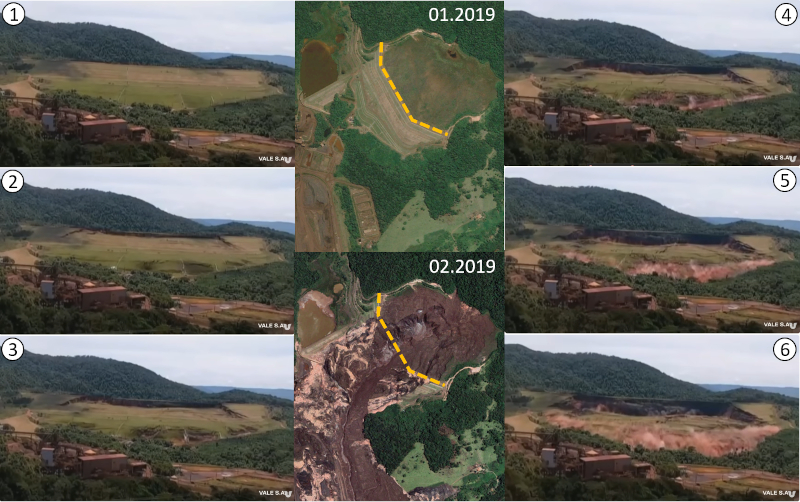
Em 25 de janeiro de 2019, a Barragem 1, que está no centro da imagem, colapsou, como mostram as imagens de 1 a 6. Inicialmente, a base começou a se mover enquanto o topo começou a afundar. Eventualmente, um fluxo de água emergiu da base enquanto toda a estrutura colapsava. Na imagem central inferior, você pode ver a situação após a barragem ter se esvaziado completamente do lado que a continha ([1], [2]):
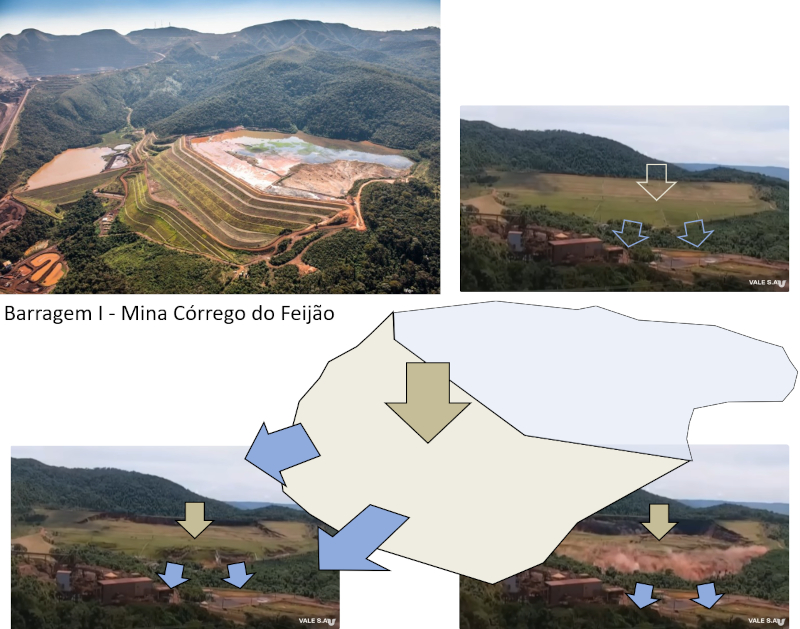
A imagem superior esquerda mostra a barragem antes do colapso, e o diagrama explica como a água pressiona a superfície da base (setas azuis) e faz com que o centro colapse (seta bege). As imagens mostram a estrutura novamente antes do colapso (foto superior direita), quando a base está sendo forçada, causando o colapso da parte superior (foto inferior esquerda) e o fluxo de água resultante na base (foto inferior direita) [3]:
A dinâmica é impulsionada pela alta pressão e alto fluxo que existem na base, explicando o surgimento da água por esse caminho.
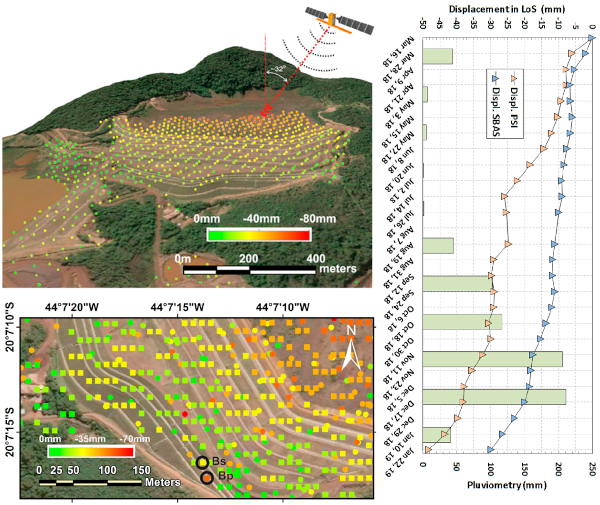
Nesse caso, houve múltiplos sinais de perigo, o que levou a um monitoramento detalhado por satélite do movimento de vários pontos por mais de um ano. Os pontos estão indicados na foto superior, e na segunda imagem à esquerda inferior, você pode ver um detalhe da base. Especificamente, os pontos que experimentaram o maior deslocamento total (Bs e Bp) são destacados, e esses pontos também são mostrados no gráfico à direita. O gráfico também mostra a quantidade de chuva, que contribui em parte, mas não é necessariamente um fator-chave [4]:
Este exemplo tem como objetivo demonstrar como a alta pressão na base, combinada com um alto fluxo de água, contribui para a dinâmica observada, sem necessariamente explicar quando ou como ela se tornou instável. Isso será explorado mais adiante.[1] Google Earth Pro para Brumadinho, Minas Gerais, Brasil, janeiro de 2019 e fevereiro de 2019[2] Câmeras da Vale S.A.[3] Procedimento Investigatório Criminal nº MPMG-0090.19.000013-4, Inquérito Policial nº PCMG-7977979, MINISTÉRIO PÚBLICO DO ESTADO DE MINAS GERAIS[4] Deformações Anteriores ao Colapso da Barragem de Brumadinho Reveladas por Dados InSAR do Sentinel-1 Usando Técnicas SBAS e PSI, Fábio F. Gama, José C. Mura, Waldir R. Paradella e Cleber G. de Oliveira, MDPI, Remote Sens. 2020, 12, 3664.
ID:(4378, 0)
Flua para um poço
Conceito 
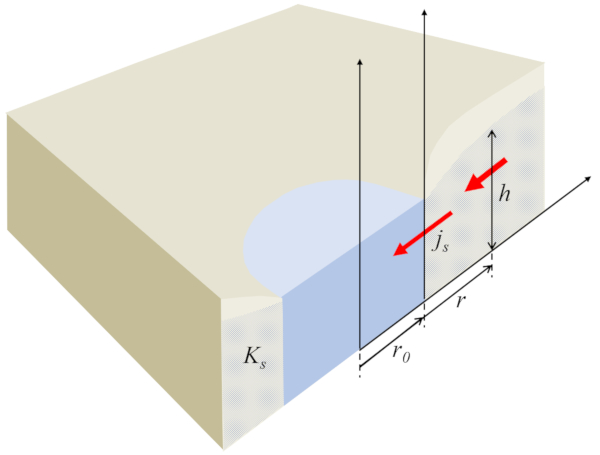
No caso do fluxo de água subterrânea em direção a um poço, la altura da coluna d'água no solo ($h$) como uma função de o raio do centro do poço ($r$) com o raio do poço de água ($r_0$), o comprimento característico do fluxo no solo ($s_0$) e la altura de referência da coluna de água ($h_0$) é representado por
| $ r \displaystyle\frac{ dh^2 }{ dr } = 2 h_0 ^2\displaystyle\frac{ r_0 }{ s_0 } $ |
o que define o perfil da água no solo:
ID:(4371, 0)
Solução de altura de fluxo em direção a um poço
Conceito 
A solução para a equação de fluxo unidimensional em direção a um poço, na qual o valor de la altura da coluna d'água no solo ($h$) é calculado como uma função de o raio do centro do poço ($r$), la altura de referência da coluna de água ($h_0$) e o raio do poço de água ($r_0$) na borda do poço, juntamente com o comprimento característico do fluxo no solo ($s_0$), tem a seguinte forma:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \displaystyle\frac{ 2 r_0 }{ s_0 }\ln\left(\displaystyle\frac{ r }{ r_0 }\right)} $ |
Esta solução é representada graficamente em termos dos fatores adicionais $h/h_0$ e $r/r_0$ para vários valores de $r_0/s_0$, da seguinte forma:
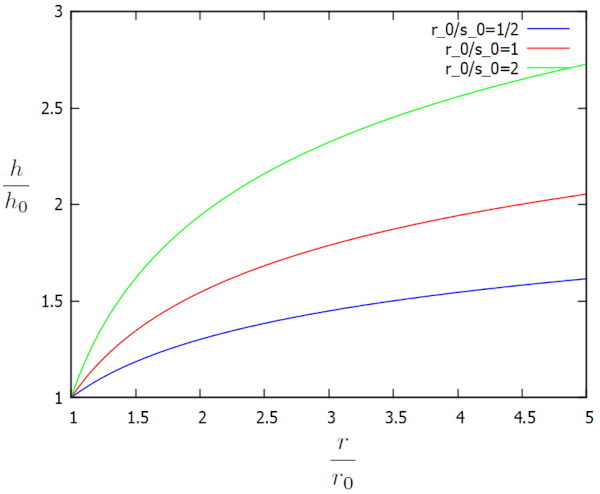
O perfil revela que, longe do poço, a altura da coluna de água é significativamente alta. No entanto, devido à extração de água pelo poço, essa altura começa a diminuir até alcançar a borda do poço. De forma dinâmica, la densidade de fluxo ($j_s$) determina a quantidade de água que flui em direção ao poço, enquanto la altura de referência da coluna de água ($h_0$) se ajusta gradualmente para atingir um estado de equilíbrio. Em outras palavras, se o valor de la altura de referência da coluna de água ($h_0$) for muito baixo em relação à quantidade total de água que chega ao poço, ele aumenta, e se for muito alto, diminui. Dessa forma, la altura de referência da coluna de água ($h_0$) adquire o valor que equilibra a quantidade de água que chega com a quantidade de água que é extraída através do poço.
ID:(10591, 0)
Solução de densidade de fluxo em direção a um poço
Conceito 
A solução obtida para a altura e os parâmetros o fluxo em um ponto de referência ($j_{s0}$) e o raio do centro do poço ($r$), o raio do poço de água ($r_0$), o comprimento característico do fluxo no solo ($s_0$) nos mostra que la densidade de fluxo ($j_s$) é igual a:
| $ \displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{1}{\displaystyle\frac{ r }{ r_0 }\sqrt{1 + \displaystyle\frac{ 2 r_0 }{ s_0 }\ln\left(\displaystyle\frac{r}{r_0}\right)}}$ |
Esta solução é representada graficamente em termos dos fatores adicionais $j_s/j_{s0}$ e $r/r_0$ para vários valores de $r_0/s_0$ da seguinte forma:
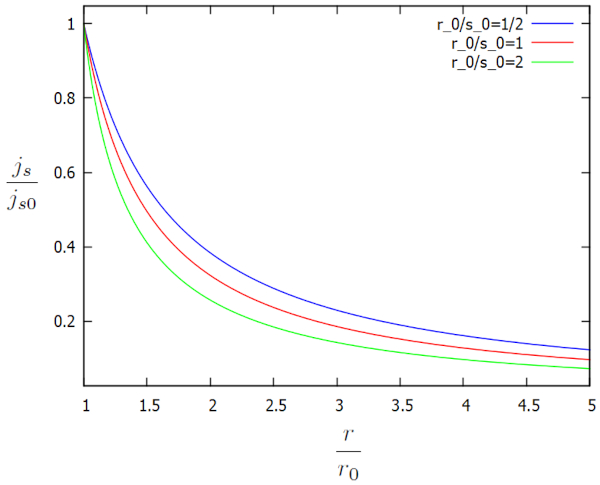
la densidade de fluxo ($j_s$) continua a aumentar à medida que nos aproximamos do canal, enquanto la altura da coluna d'água no solo ($h$) diminui. Esse aumento é necessário para manter a velocidade do fluxo em la densidade de fluxo ($j_s$) ou, alternativamente, para aumentá-la.
ID:(2209, 0)
