Benützer:
Sonnen- und Mondfluten
Storyboard 
Der zweite Typ von Gezeiten, der auf der Erde registriert wird, sind die Sonnen-Gezeiten. Ihre Größe ist kleiner als die des Mondes.
ID:(1576, 0)
Sonnen- und Mondfluten
Storyboard
Der zweite Typ von Gezeiten, der auf der Erde registriert wird, sind die Sonnen-Gezeiten. Ihre Größe ist kleiner als die des Mondes.
Variablen
Berechnungen
zu 
,
dann die Variable auswählen: 
zu 
Berechnungen
Variable
Gegeben
Berechnen
Ziel :
Gleichung
Zu verwenden
Gleichungen
Beispiele
Die Ver nderung der Gravitationsbeschleunigung f hrt zu einem Wasserfluss, der dazu neigt, die H he der Wassers ule (Meerestiefe) zu ver ndern, um den Druck auszugleichen:
Variationen in der Beschleunigung f hren dazu, dass der Druck auf das Wasser um den Planeten herum variiert und es erm glicht, dass sich die Wasserstrahlen in ihrer H he unterscheiden.
Insbesondere sind die verursachten Abweichungen wie folgt:
F r den Fall der Sonne: 8,14 cm, 16,28 cm
F r den Fall des Mondes: 17,9 cm, 35,6 cm
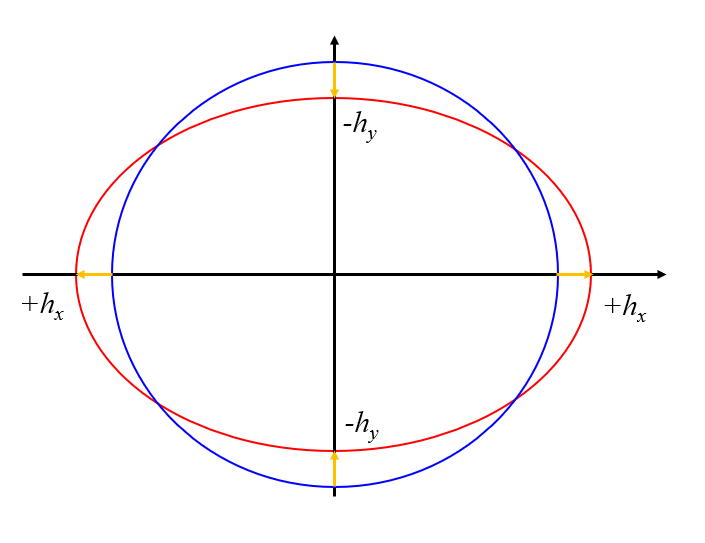
Diese Situation kann als Verformung eines Kreises dargestellt werden, was einer Ellipse entspricht.
Im Fall der Sonne,
werden folgende Parameter ber cksichtigt:
Masse: 1,987e+30 kg
Sonne-Erde-Abstand: 1,50e+11 m
Die Gezeitenh hen k nnen mithilfe der folgenden Beziehungen berechnet werden:
F r die x-Richtung, mit
Und f r die y-Richtung, mit
Mit dem Erdradius von 6371 km erhalten wir am Punkt der minimalen Gezeiten ($\theta = \pi/2$):
$h_y = 8,14 cm$
Und am Punkt der maximalen Gezeiten ($\theta = 0$) gilt:
$h_x = 16,28 cm$
Somit betragen die Schwankungen aufgrund der Sonne $h_x + h_y = 24,42 cm$.
Im Falle des Mondes,
sind die Parameter:
Masse: 7,349e+22 kg
Entfernung Erde-Mond: 3,84e+8 m
F r die Richtung x, mit
Und f r die Richtung y, mit
Mit dem Erdradius von 6371 km erhalten wir f r den Punkt mit niedrigster Flut ($\theta = \pi/2$):
$h_y = 17,9 cm$
Und f r den Punkt mit h chster Flut ($\theta = 0$) haben wir:
$h_x = 35,6 cm$
Daher betragen die Fluktuationen aufgrund des Mondes $h_x + h_y = 53,5 cm$.
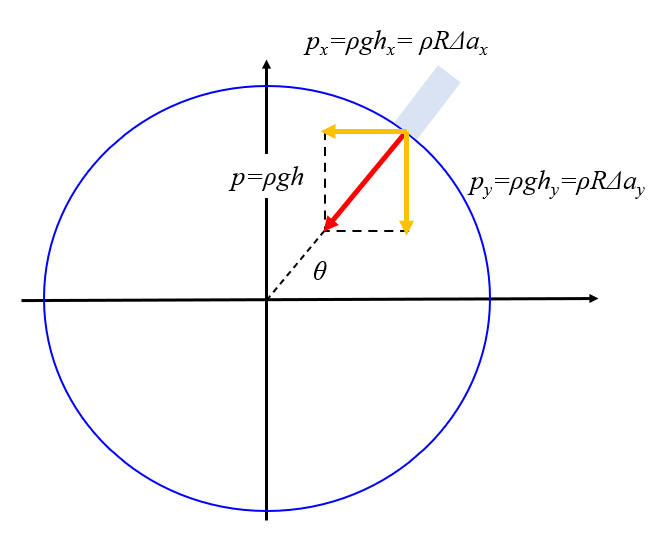
Die nderung in der Beschleunigung bedeutet, dass die Wassers ule einen anderen Druck erf hrt, es sei denn, die Tiefe passt sich an. Um einen station ren Zustand zu erreichen, ist genau dies der Fall. Die nderung der Gravitationsbeschleunigung wird durch eine nderung der Tiefe kompensiert, die der Gezeiten entspricht:
$p_x=\rho g h_x=\rho\displaystyle\frac{1}{2} (\Delta a_{cx} - \Delta a_{ox}) R$
Daher,
Die nderung in der Beschleunigung bedeutet, dass die Wassers ule eine unterschiedliche Druck erf hrt, es sei denn, die Tiefe passt sich an. Um einen stabilen Zustand zu erreichen, geschieht genau das. Die nderung der Gravitationsbeschleunigung wird durch eine nderung in der Tiefe kompensiert, die der Gezeiten entspricht:
Mit der Variation auf der Konjunktionseite mit
und mit
Es ergibt sich, dass die Oberfl che mit
wobei nur der variable Teil der Variation ber cksichtigt wurde, da der Term $GM/d^2$ auf das gesamte System wirkt und keine Unterschiede erzeugt.
Die nderung in der Beschleunigung bedeutet, dass die Wassers ule einen unterschiedlichen Druck erf hrt, es sei denn, die Tiefe passt sich an. Um einen stabilen Zustand zu erreichen, geschieht genau das. Die Modifikation der Gravitationsbeschleunigung wird durch eine nderung in der Tiefe kompensiert, die der Gezeiten entspricht:
$p_y=\rho g h_y=\rho\Delta a_{cy} R$
Daher ergibt sich:
Die nderung der Beschleunigung bedeutet, dass die Wassers ule einen anderen Druck erf hrt, es sei denn, die Tiefe passt sich an. Um einen stabilen Zustand zu erreichen, ist genau das der Fall. Die Modifikation der Gravitationsbeschleunigung wird durch eine nderung der Tiefe ausgeglichen, die der Gezeiten entspricht:
Mit der Variation auf der Seite der Konjunktion mit
Daraus ergibt sich, dass die Oberfl che mit
Mit der Ver nderung des Meeresspiegels durch Mond- und/oder Sonnentiden, die eine Funktion von die Universelle Gravitationskonstante ($G$), der Planetenradio ($R$), die Entfernung des Himmelsobjektplaneten ($d$), die Gravitationsbeschleunigung ($g$) und die Breitengrad des Ortes ($\theta$) ist, ergibt sich in Richtung des Himmelsk rpers, der die Tide verursacht, eine Tidenh he von die Höhe der Flut in Richtung des Sterns ($h_x$), berechnet mit:
In der senkrechten Richtung betr gt die entsprechende H he die Höhe der Flut senkrecht zur Richtung zum Stern ($h_y$):
Daher wird der Gesamtabstand aus die Höhe der Flut in Richtung des Sterns ($h_x$) und die Höhe der Flut senkrecht zur Richtung zum Stern ($h_y$) berechnet:
ID:(1576, 0)
