(ID 15441)

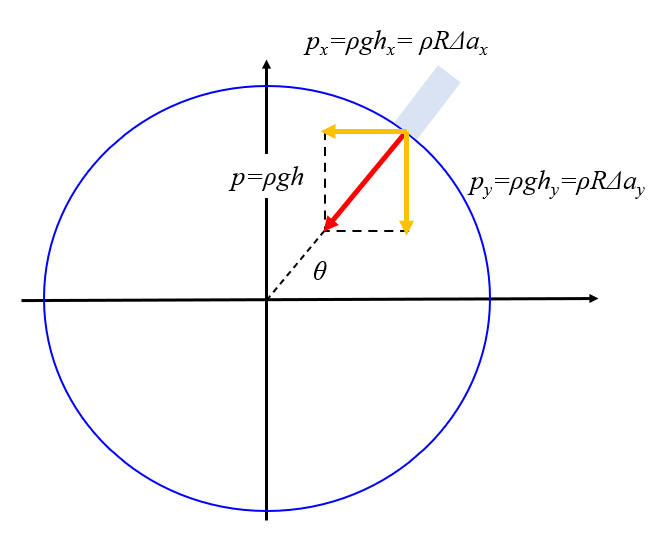
Le changement dans l'acc l ration gravitationnelle entra ne un flux d'eau qui a tendance modifier la hauteur de la colonne d'eau (profondeur de la mer) afin de compenser la pression :

(ID 11652)

Les variations d'acc l ration entra nent des changements de pression sur l'eau autour de la plan te, permettant ainsi aux colonnes d'eau de diff rer en hauteur.

En particulier, les d viations caus es sont les suivantes :

Pour le cas du soleil : 8,14 cm, 16,28 cm
Pour le cas de la lune : 17,9 cm, 35,6 cm

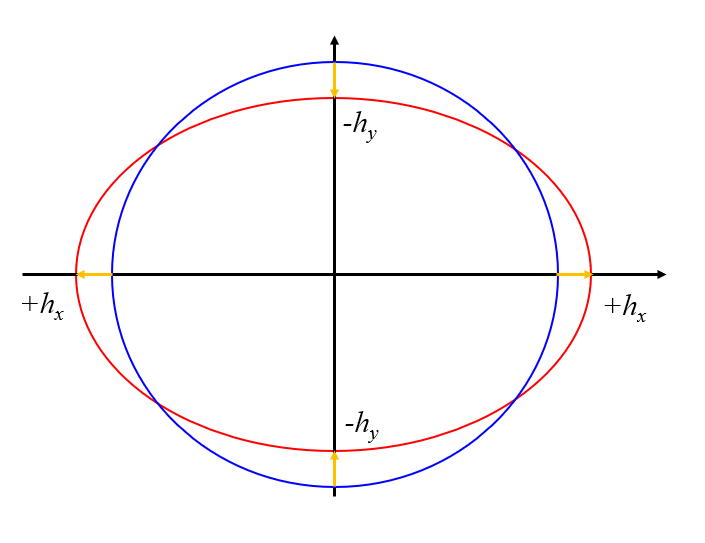
Cette situation peut tre repr sent e comme une d formation d'un cercle, correspondant une ellipse.

(ID 11657)

Dans le cas du Soleil,

les param tres consid r s sont :

Masse : 1,987e+30 kg
Distance Soleil-Terre : 1,50e+11 m
Les hauteurs des mar es peuvent tre calcul es avec les relations suivantes :

Pour la direction x, avec hauteur de la marée dans la direction de l'étoile $m$, latitude du lieu $rad$ et rayon de la planète $m$, nous avons :

$h_x = \displaystyle\frac{2 G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\cos\theta $

Et pour la direction y, avec hauteur de la marée perpendiculaire à la direction vers l'étoile $m$, latitude du lieu $rad$ et rayon de la planète $m$, nous avons :

$h_y = \displaystyle\frac{ G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\sin\theta$

Avec le rayon de la Terre de 6371 km, nous obtenons que au point de mar e basse ($\theta = \pi/2$), nous avons :

$h_y = 8,14 cm$

Et au point de mar e haute ($\theta = 0$), nous avons :

$h_x = 16,28 cm$

Ainsi, les fluctuations dues au Soleil sont de $h_x + h_y = 24,42 cm$.

(ID 11656)

Dans le cas de la lune,

les param tres consid r s sont :

Masse : 7,349e+22 kg
Distance Terre-Lune : 3,84e+8 m

Pour la direction x, avec hauteur de la marée dans la direction de l'étoile $m$, latitude du lieu $rad$ et rayon de la planète $m$, nous avons :

$h_x = \displaystyle\frac{2 G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\cos\theta $

Et pour la direction y, avec hauteur de la marée perpendiculaire à la direction vers l'étoile $m$, latitude du lieu $rad$ et rayon de la planète $m$, nous avons :

$h_y = \displaystyle\frac{ G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\sin\theta$

Avec le rayon de la Terre de 6371 km, nous obtenons que au point de mar e basse ($\theta = \pi/2$), nous avons :

$h_y = 17,9 cm$

Et au point de mar e haute ($\theta = 0$), nous avons :

$h_x = 35,6 cm$

Ainsi, les fluctuations dues la lune sont de $h_x + h_y = 53,5 cm$.

(ID 11655)

(ID 15437)

Le changement dans l'acc l ration signifie que la colonne d'eau subit une pression diff rente moins que la profondeur ne s'ajuste. Pour atteindre un tat stable, c'est pr cis ment ce qui se passe. La modification de l'acc l ration gravitationnelle est compens e par un changement de profondeur correspondant la mar e :

$p_x=\rho g h_x=\rho\displaystyle\frac{1}{2} (\Delta a_{cx} - \Delta a_{ox}) R$

Par cons quent,

$ g h_x =\displaystyle\frac{1}{2}( \Delta a_{cx} - \Delta a_{ox} ) R $

(ID 13215)

Le changement dans l'acc l ration implique que la colonne d'eau subit une pression diff rente moins que la profondeur ne s'ajuste. Pour atteindre un tat stable, c'est pr cis ment ce qui se produit. La modification de l'acc l ration gravitationnelle est compens e par un changement de profondeur correspondant la mar e :

$ g h_x =\displaystyle\frac{1}{2}( \Delta a_{cx} - \Delta a_{ox} ) R $

Avec la variation du c t de la conjonction avec

$ \Delta a_{cx} = \displaystyle\frac{ G M }{ d ^2}\left(1+\displaystyle\frac{2 R \cos \theta }{ d }\right)$

et avec

$ \Delta a_{ox} =\displaystyle\frac{ G M }{ d ^2}\left(1-\displaystyle\frac{2 R \cos \theta }{ d }\right)$

Il en r sulte que la surface s' l ve avec en

$h_x = \displaystyle\frac{2 G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\cos\theta $

o seule la partie variable de la variation a t prise en compte, car le terme $GM/d^2$ agit sur tout le syst me et ne cr e pas de diff rences.

(ID 11653)

Le changement dans l'acc l ration signifie que la colonne d'eau pr sente une pression diff rente moins que la profondeur ne s'adapte. Pour atteindre un tat stationnaire, c'est pr cis ment ce qui se produit. La modification de l'acc l ration gravitationnelle est compens e par un changement de profondeur correspondant la mar e :

$p_y=\rho g h_y=\rho\Delta a_{cy} R$

Par cons quent, on a :

$ g h_y = \Delta a_{cy} R $

(ID 13216)

Le changement d'acc l ration signifie que la colonne d'eau subit une pression diff rente moins que la profondeur ne s'ajuste. Pour atteindre un tat stable, c'est pr cis ment ce qui se produit. La modification de l'acc l ration gravitationnelle est compens e par un changement de profondeur correspondant la mar e :

$ g h_y = \Delta a_{cy} R $

Avec la variation du c t de la conjonction avec

$ \Delta a_{cy} = \displaystyle\frac{ G M }{ d ^2 }\displaystyle\frac{ R \sin \theta }{ d }$

En cons quence, la surface s' l ve avec

$h_y = \displaystyle\frac{ G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\sin\theta$

(ID 11654)

Avec la variation du niveau de la mer due aux mar es lunaires et/ou solaires, qui d pend de ERROR:8564, le rayon de la planète ($R$), ERROR:8567, a accélération gravitationnelle ($g$) et a latitude du lieu ($\theta$), la hauteur de mar e dans la direction de lastre g n rateur est a hauteur de la marée dans la direction de l'étoile ($h_x$), calcul e comme suit :

$h_x = \displaystyle\frac{2 G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\cos\theta $

Dans la direction perpendiculaire, la hauteur correspondante est a hauteur de la marée perpendiculaire à la direction vers l'étoile ($h_y$) :

$h_y = \displaystyle\frac{ G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\sin\theta$

La diff rence totale est donc d termin e partir de a hauteur de la marée dans la direction de l'étoile ($h_x$) et a hauteur de la marée perpendiculaire à la direction vers l'étoile ($h_y$) :

$ h = h_x + h_y $

(ID 16135)