Benützer:
Schwerkraft und Gezeiten in Oposition
Storyboard 
Eine der Beschleunigungen, die berechnet werden müssen, ist diejenige, die parallel zur Ekliptik (in der Ebene Erde-Himmelskörper) in Opposition steht, das heißt auf der gegenüberliegenden Seite des Himmelskörpers.
ID:(1575, 0)
Variation der Schwerkraft parallel zum Radius im Gegensatz zu
Bild
Die Anziehungskraft auf der gegenüberliegenden Seite des Himmelskörpers, die auf die Erde wirkt, ist aufgrund der größeren Entfernung geringer. Dies erleichtert die Verschiebung von Wasser zum Äquator hin. Auf der dem Himmelskörper zugewandten Seite schwächt seine Anziehungskraft die Gravitationsbeschleunigung der Erde, was wiederum zu einer Verringerung der Schwerkraft führt, die die Verschiebung des Wassers zum Äquator hin begünstigt:
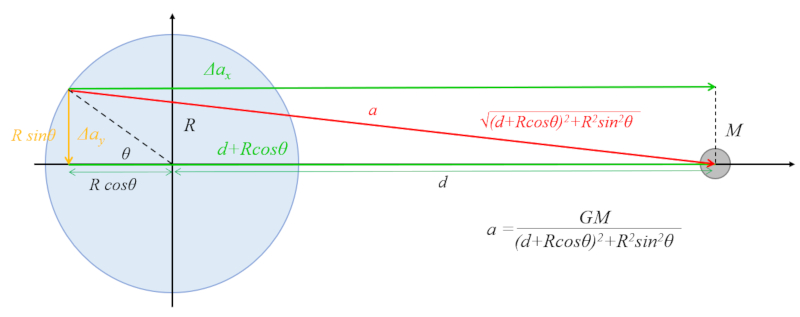
In diesem Fall arbeiten wir mit der Ähnlichkeit im Dreieck, bei der wir das Verhältnis
$\Delta a_{ox}/a_o$
und das Kathete
$d + R\cos\theta$
und die Hypotenuse
$(d+R\cos\theta)^2+R^2\sin^2\theta=d^2+R^2+2dR\cos\theta$
ID:(11639, 0)
Intuitive Erklärung der Flut auf der dem Himmelskörper gegenüberliegenden Seite
Bild
Es gibt mehrere Erklärungen für die Gezeiten auf der dem Himmelskörper gegenüberliegenden Seite. Eine davon ist der Effekt der Zentrifugalkraft aufgrund der Tatsache, dass das System um den Massenschwerpunkt des Systems Erde-Himmelskörper rotiert, der nicht im Zentrum der Erde liegt. Die Werte für den Fall des Mondes sind jedoch sehr unterschiedlich auf der der Mond zugewandten Seite im Vergleich zur dem Mond abgewandten Seite der Erde. Darüber hinaus wäre es schwierig, das Phänomen auf diese Weise zu erklären, wenn man die Sonne als den Himmelskörper betrachtet, da sich der Massenschwerpunkt in diesem Fall in der Nähe des Zentrums der Sonne befindet.
Die einfachste und am besten beobachteten Werte liefernde Erklärung ist, anzunehmen, dass es sich um ein Problem der Gravitationsunterschiede und der Verschiebung der Objekte handelt. Daher:
• Die Flutwelle auf der Seite des Himmelskörpers entsteht durch dessen Anziehungskraft, die die Gravitationsbeschleunigung der Erde reduziert.
• Die Flutwelle auf der dem Himmelskörper gegenüberliegenden Seite entsteht sowohl durch die Reduzierung der Anziehungskraft des Himmelskörpers als auch durch die Tatsache, dass die Erde "im Wasser" verschoben wird.
ID:(11640, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ a_o = \displaystyle\frac{ G M }{ d ^2+ R ^2+2 d R \cos \theta }$
a_o = G * M /( d ^2 + R ^2 + 2* d * R * cos( theta ))
$ \displaystyle\frac{ \Delta a_{ox} }{ a_o } =\displaystyle\frac{ d + R\cos\theta }{ \sqrt{ d ^2+ R ^2+2 d R \cos \theta } }$
Da_ox / a_o = ( d + R * cos( theta ))/sqrt( d ^2 + R ^2 + 2 * d * R * cos( theta ))
$ \Delta a_{ox} =\displaystyle\frac{ G M }{ d ^2}\left(1-\displaystyle\frac{2 R \cos \theta }{ d }\right)$
Da_ox = G * M * (1-2* R * cos( theta )/ d )/ d ^2
ID:(15435, 0)
Variation der Beschleunigung parallel zum Radius im Gegensatz zu
Gleichung
Um die Variation der Beschleunigung im Radius zu bestimmen, können wir die Beziehung
$\displaystyle\frac{\Delta a_{ox}}{a_o}$
mit der Länge
$d+R\cos\theta$
und der Hypotenuse
$\sqrt{d^2+R^2+2dR\cos\theta}$
Durch die Ähnlichkeit der Dreiecke erhalten wir mit , dass:
| $ \displaystyle\frac{ \Delta a_{ox} }{ a_o } =\displaystyle\frac{ d + R\cos\theta }{ \sqrt{ d ^2+ R ^2+2 d R \cos \theta } }$ |
ID:(11646, 0)
Beschleunigung parallel zum Radius im Gegensatz zu
Gleichung
Mit dem Gravitationsgesetz von Newton, repräsentiert durch ,
| $ F = G \displaystyle\frac{ m_g M }{ r ^2}$ |
,
können wir die Kraft mit definieren,
| $ F = m_i a $ |
,
und den quadratischen Radius
$r^2=d^2+R^2+2dR\cos\theta$
,
um mit die Beschleunigung zu berechnen:
| $ a_o = \displaystyle\frac{ G M }{ d ^2+ R ^2+2 d R \cos \theta }$ |
ID:(11651, 0)
Beschleunigungsnäherung parallel zum Radius in Oposition
Gleichung
Mit beschleunigungsvariation parallel zur Ekliptik, in Oposition $m/s^2$, entfernung des Himmelsobjektplaneten $m$, planetenradio $m$, vom Himmelskörper erzeugte Beschleunigung, in Opotion $m/s^2$ und winkel von der Planetenlinie - Himmelsobjekt $rad$ ist die Beziehung
| $ \displaystyle\frac{ \Delta a_{ox} }{ a_o } =\displaystyle\frac{ d + R\cos\theta }{ \sqrt{ d ^2+ R ^2+2 d R \cos \theta } }$ |
,
und mit entfernung des Himmelsobjektplaneten $m$, masa del cuerpo que genera la marea $kg$, planetenradio $m$, universelle Gravitationskonstante $m^3/kg s^2$, vom Himmelskörper erzeugte Beschleunigung, in Opotion $m/s^2$ und winkel von der Planetenlinie - Himmelsobjekt $rad$ ist der Ausdruck
| $ a_o = \displaystyle\frac{ G M }{ d ^2+ R ^2+2 d R \cos \theta }$ |
,
dann
$\Delta a_{ox} =GM\displaystyle\frac{d + R\cos\theta}{(d^2 + R^2 + 2dR\cos\theta)^{3/2}}\sim \displaystyle\frac{GM}{d^2}\left(1-\displaystyle\frac{2R\cos\theta}{d}\right)$
,
also in der Näherung $d\gg R$ und unter Berücksichtigung nur der Variation in Bezug auf die gegenüberliegende Seite, kann es mit entfernung des Himmelsobjektplaneten $m$, masa del cuerpo que genera la marea $kg$, planetenradio $m$, universelle Gravitationskonstante $m^3/kg s^2$, vom Himmelskörper erzeugte Beschleunigung, in Opotion $m/s^2$ und winkel von der Planetenlinie - Himmelsobjekt $rad$ approximiert werden als:
| $ \Delta a_{ox} =\displaystyle\frac{ G M }{ d ^2}\left(1-\displaystyle\frac{2 R \cos \theta }{ d }\right)$ |
ID:(11649, 0)