Mareas solares y lunares
Storyboard 
El segundo tipo de mareas que se registran en la Tierra son las mareas solares. Su tamaño es menor que el de la luna.
ID:(1576, 0)
Profundidad del agua necesaria para compensar
Imagen 
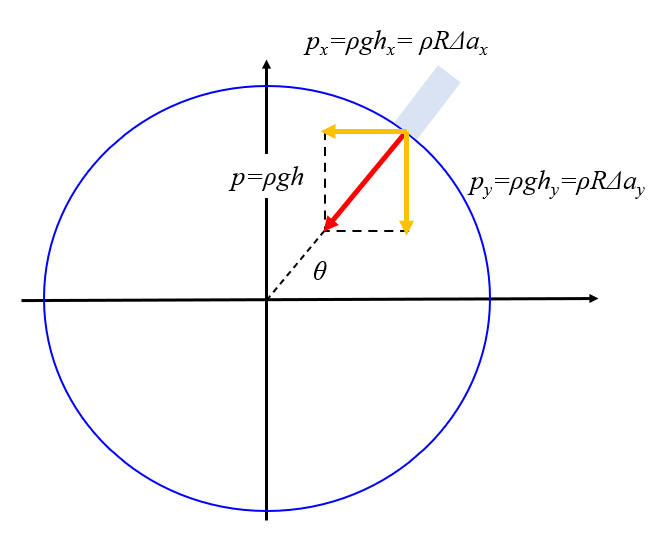
La variación en la aceleración gravitacional provoca un flujo de agua que tiende a cambiar la altura de la columna de agua (profundidad del mar) para compensar la presión:
ID:(11652, 0)
Representación como elipse
Nota 
Las variaciones en la aceleración provocan que la presión sobre el agua varíe alrededor del planeta, lo que permite que las columnas de agua difieran en alturas.
En particular, los desvíos causados son los siguientes:
Para el caso del sol: 8.14 cm, 16.28 cm
Para el caso de la luna: 17.9 cm, 35.6 cm
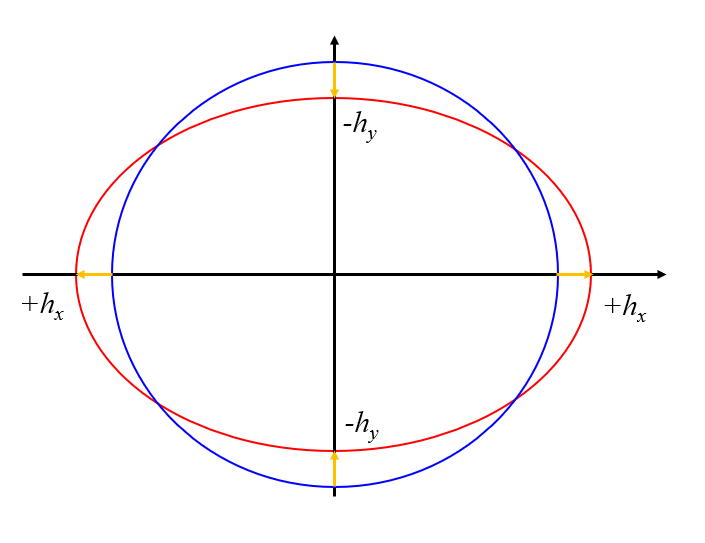
Esta situación se puede representar como una deformación de un círculo, lo que corresponde a una elipse.
ID:(11657, 0)
Parámetros caso sol
Cita 
En el caso del sol,

se tienen los siguientes parámetros:
Masa: 1.987e+30 kg
Distancia sol-tierra: 1.50e+11 m
Las alturas de las mareas se pueden calcular utilizando las siguientes relaciones:
Para la dirección x, con , se tiene:
| $h_x = \displaystyle\frac{2 G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\cos\theta $ |
Y para la dirección y, con , se obtiene:
| $h_y = \displaystyle\frac{ G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\sin\theta$ |
Con el radio de la Tierra de 6371 km, se obtiene que en el punto de menor marea ($\theta = \pi/2$), se tiene:
$h_y = 8.14 cm$
Y en el punto de máxima marea ($\theta = 0$), es:
$h_x = 16.28 cm$
Es decir, las fluctuaciones debidas al sol son de $h_x + h_y = 24.42 cm$.
ID:(11656, 0)
Parámetros caso luna
Ejercicio 
En el caso de la Luna,
tenemos los siguientes parámetros:
Masa: 7.349e+22 kg
Distancia Tierra-Luna: 3.84e+8 m
Para la dirección x, con , tenemos:
| $h_x = \displaystyle\frac{2 G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\cos\theta $ |
Y para la dirección y, con , obtenemos:
| $h_y = \displaystyle\frac{ G M }{ g }\displaystyle\frac{ R ^2}{ d ^3}\sin\theta$ |
Con el radio de la Tierra de 6371 km, en el punto de marea más baja ($\theta = \pi/2$), obtenemos:
$h_y = 17.9 cm$
Y en el punto de marea más alta ($\theta = 0$), tenemos:
$h_x = 35.6 cm$
Por lo tanto, las fluctuaciones debidas a la Luna suman $h_x + h_y = 53.5 cm$.
ID:(11655, 0)
Mareas solares y lunares
Storyboard 
El segundo tipo de mareas que se registran en la Tierra son las mareas solares. Su tamaño es menor que el de la luna.
Variables
Cálculos
Cálculos
Ecuaciones
Ejemplos
La variaci n en la aceleraci n gravitacional provoca un flujo de agua que tiende a cambiar la altura de la columna de agua (profundidad del mar) para compensar la presi n:
Las variaciones en la aceleraci n provocan que la presi n sobre el agua var e alrededor del planeta, lo que permite que las columnas de agua difieran en alturas.
En particular, los desv os causados son los siguientes:
Para el caso del sol: 8.14 cm, 16.28 cm
Para el caso de la luna: 17.9 cm, 35.6 cm
Esta situaci n se puede representar como una deformaci n de un c rculo, lo que corresponde a una elipse.
En el caso del sol,
se tienen los siguientes par metros:
Masa: 1.987e+30 kg
Distancia sol-tierra: 1.50e+11 m
Las alturas de las mareas se pueden calcular utilizando las siguientes relaciones:
Para la direcci n x, con
Y para la direcci n y, con
Con el radio de la Tierra de 6371 km, se obtiene que en el punto de menor marea ($\theta = \pi/2$), se tiene:
$h_y = 8.14 cm$
Y en el punto de m xima marea ($\theta = 0$), es:
$h_x = 16.28 cm$
Es decir, las fluctuaciones debidas al sol son de $h_x + h_y = 24.42 cm$.
En el caso de la Luna,
tenemos los siguientes par metros:
Masa: 7.349e+22 kg
Distancia Tierra-Luna: 3.84e+8 m
Para la direcci n x, con
Y para la direcci n y, con
Con el radio de la Tierra de 6371 km, en el punto de marea m s baja ($\theta = \pi/2$), obtenemos:
$h_y = 17.9 cm$
Y en el punto de marea m s alta ($\theta = 0$), tenemos:
$h_x = 35.6 cm$
Por lo tanto, las fluctuaciones debidas a la Luna suman $h_x + h_y = 53.5 cm$.
El cambio en la aceleraci n implica que la columna de agua experimenta una presi n diferente a menos que la profundidad se ajuste. Para alcanzar un estado estacionario, esto es precisamente lo que sucede. La modificaci n de la aceleraci n gravitacional es compensada por un cambio en la profundidad que corresponde a la marea:
$p_x=\rho g h_x=\rho\displaystyle\frac{1}{2} (\Delta a_{cx} - \Delta a_{ox}) R$
Por lo tanto,
El cambio en la aceleraci n implica que la columna de agua experimenta una presi n diferente a menos que la profundidad se ajuste. Para alcanzar un estado estacionario, esto es precisamente lo que ocurre. La modificaci n de la aceleraci n gravitacional es compensada por un cambio en la profundidad que corresponde a la marea:
Con la variaci n en el lado de la conjunci n con
y con
Se tiene que la superficie asciende con
donde solo se tom la parte que var a de la variaci n, ya que el t rmino $GM/d^2$ act a sobre todo el sistema y no crea diferencias.
El cambio en la aceleraci n implica que la columna de agua experimenta una presi n diferente a menos que la profundidad se ajuste. Para alcanzar un estado estacionario, esto es precisamente lo que sucede. La modificaci n de la aceleraci n gravitacional se compensa con un cambio en la profundidad que corresponde a la marea:
$p_y=\rho g h_y=\rho\Delta a_{cy} R$
Por lo tanto, se deduce que:
El cambio en la aceleraci n implica que la columna de agua experimenta una presi n diferente a menos que la profundidad se ajuste. Para alcanzar un estado estacionario, esto es precisamente lo que ocurre. La modificaci n de la aceleraci n gravitacional es compensada por un cambio en la profundidad que corresponde a la marea:
Con la variaci n en el lado de la conjunci n con
Como resultado, la superficie se eleva con
Con la variaci n del nivel del mar debido a las mareas lunares y/o solares, que es funci n de la constante Universal de Gravitación ($G$), el radio del planeta ($R$), la distancia planeta objeto celeste ($d$), la aceleración gravitacional ($g$) y la latitud del lugar ($\theta$), se obtiene una altura de marea en la direcci n del astro que genera la marea igual a la altura de la marea en direccion al astro ($h_x$), la cual se calcula mediante:
En la direcci n perpendicular, la altura correspondiente es la altura de la marea perpendicular a la dirección hacia el astro ($h_y$):
Por lo tanto, la diferencia total se obtiene a partir de la altura de la marea en direccion al astro ($h_x$) y la altura de la marea perpendicular a la dirección hacia el astro ($h_y$):
ID:(1576, 0)
