Usuario:
Fuerza de gravedad y mareas en oposición
Storyboard 
Una de las aceleraciones que se debe calcular es aquella paralela a la eclíptica (en el plano Tierra-cuerpo celeste) en oposición, es decir, en el lado opuesto al lado donde se encuentra el cuerpo celeste.
ID:(1575, 0)
Variación de la gravedad paralelo al radio, en oposición
Imagen
La atracción en el lado opuesto al cuerpo celeste que actúa sobre la Tierra es menor debido a que la distancia es mayor. Esto facilita el desplazamiento del agua hacia el ecuador. Por otro lado, en el lado del cuerpo celeste, su atracción debilita la aceleración gravitacional de la Tierra, lo que a su vez conduce a una reducción de la gravedad que favorece el movimiento del agua hacia el ecuador:
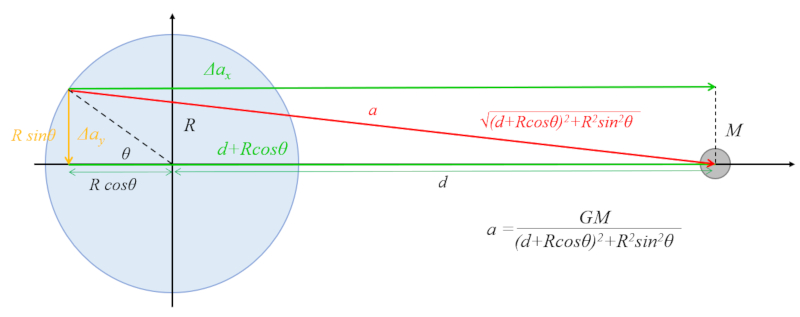
En este caso, se trabaja con la similitud en el triángulo donde se toma la proporción
$\Delta a_{ox}/a_o$
y el cateto
$d + R\cos\theta$
y la hipotenusa
$(d+R\cos\theta)^2+R^2\sin^2\theta=d^2+R^2+2dR\cos\theta$
ID:(11639, 0)
Explicación intuitiva de la marea en el lado opuesto al cuerpo celeste
Imagen
Existen múltiples explicaciones sobre las mareas en el lado opuesto del cuerpo celeste. Una de ellas es que es el efecto de la aceleración centrífuga por el hecho de que el sistema gira en torno al centro de masa del sistema tierra-cuerpo celeste que no se encuentra en el centro de la tierra. Sin embargo los valores que se obtienen para el caso de la luna son muy distintos en el lado hacia la luna que en el lado opuesto de la tierra. Adicionalmente seria complicado explicar el fenómeno de esta forma si se toma el sol como cuerpo celeste ya que en ese caso el centro de masa es próximo al centro del sol.
La forma más simple y que arroja valores como los observados es suponer que es un problema de diferencias de gravedad y desplazamiento de los objetos por ello:
• la marea hacia el lado del cuerpo celeste se origina por la atracción de este que reduce la aceleración gravitacional de la tierra
• la marea en el lado opuesto del cuerpo celeste se da tanto por la reducción de la atracción del cuerpo celeste pero también por efecto de que la tierra es desplazada 'dentro del agua'
ID:(11640, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ a_o = \displaystyle\frac{ G M }{ d ^2+ R ^2+2 d R \cos \theta }$
a_o = G * M /( d ^2 + R ^2 + 2* d * R * cos( theta ))
$ \displaystyle\frac{ \Delta a_{ox} }{ a_o } =\displaystyle\frac{ d + R\cos\theta }{ \sqrt{ d ^2+ R ^2+2 d R \cos \theta } }$
Da_ox / a_o = ( d + R * cos( theta ))/sqrt( d ^2 + R ^2 + 2 * d * R * cos( theta ))
$ \Delta a_{ox} =\displaystyle\frac{ G M }{ d ^2}\left(1-\displaystyle\frac{2 R \cos \theta }{ d }\right)$
Da_ox = G * M * (1-2* R * cos( theta )/ d )/ d ^2
ID:(15435, 0)
Variación de aceleración paralelo al radio, en oposición
Ecuación
Para determinar la variación de la aceleración en el radio, podemos igualar la relación
$\displaystyle\frac{\Delta a_{ox}}{a_o}$
con el largo
$d+R\cos\theta$
y la hipotenusa
$\sqrt{d^2+R^2+2dR\cos\theta}$
Por similitud de triángulos, se obtiene con que:
| $ \displaystyle\frac{ \Delta a_{ox} }{ a_o } =\displaystyle\frac{ d + R\cos\theta }{ \sqrt{ d ^2+ R ^2+2 d R \cos \theta } }$ |
ID:(11646, 0)
Aceleración paralelo al radio, en oposición
Ecuación
Con la ley de la gravitación de Newton, representada por ,
| $ F = G \displaystyle\frac{ m_g M }{ r ^2}$ |
podemos definir la fuerza con ,
| $ F = m_i a $ |
y el radio al cuadrado
$r^2=d^2+R^2+2dR\cos\theta$
para calcular con la aceleración:
| $ a_o = \displaystyle\frac{ G M }{ d ^2+ R ^2+2 d R \cos \theta }$ |
ID:(11651, 0)
Aproximación aceleración paralelo al radio, en oposición
Ecuación
Con aceleración generada por el cuerpo celeste, en oposition $m/s^2$, ángulo desde la línea planeta - objeto celeste $rad$, distancia planeta objeto celeste $m$, radio del planeta $m$ y variación de aceleración paralelo a la eclíptica, en oposición $m/s^2$, la relación es
| $ \displaystyle\frac{ \Delta a_{ox} }{ a_o } =\displaystyle\frac{ d + R\cos\theta }{ \sqrt{ d ^2+ R ^2+2 d R \cos \theta } }$ |
,
y con aceleración generada por el cuerpo celeste, en oposition $m/s^2$, ángulo desde la línea planeta - objeto celeste $rad$, constante Universal de Gravitación $m^3/kg s^2$, distancia planeta objeto celeste $m$, masa del cuerpo que genera la marea $kg$ y radio del planeta $m$, la expresión es
| $ a_o = \displaystyle\frac{ G M }{ d ^2+ R ^2+2 d R \cos \theta }$ |
,
entonces
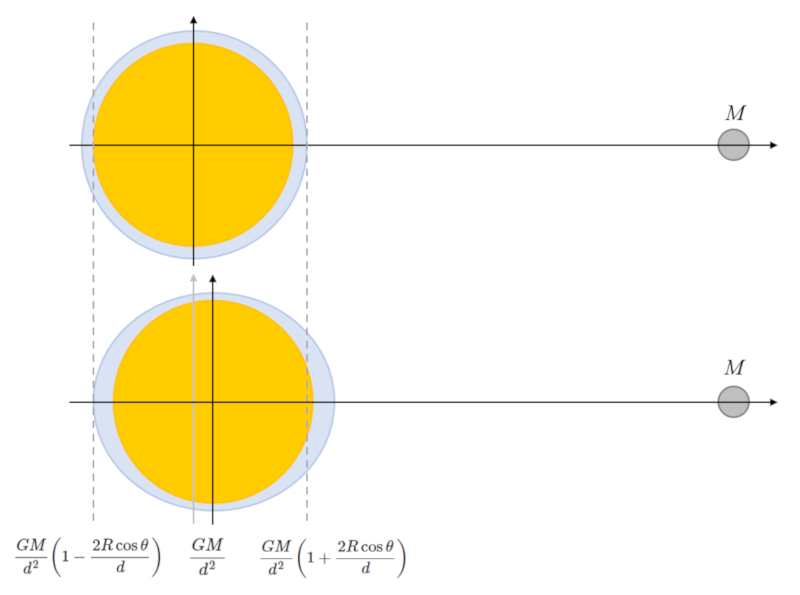
$\Delta a_{ox} =GM\displaystyle\frac{d + R\cos\theta}{(d^2 + R^2 + 2dR\cos\theta)^{3/2}}\sim \displaystyle\frac{GM}{d^2}\left(1-\displaystyle\frac{2R\cos\theta}{d}\right)$
,
por lo que en la aproximación $d\gg R$ y solo considerando la variación respecto al lado opuesto, se puede aproximar con aceleración generada por el cuerpo celeste, en oposition $m/s^2$, ángulo desde la línea planeta - objeto celeste $rad$, constante Universal de Gravitación $m^3/kg s^2$, distancia planeta objeto celeste $m$, masa del cuerpo que genera la marea $kg$ y radio del planeta $m$:
| $ \Delta a_{ox} =\displaystyle\frac{ G M }{ d ^2}\left(1-\displaystyle\frac{2 R \cos \theta }{ d }\right)$ |
ID:(11649, 0)