Vapor de Agua
Storyboard 
La evaporación de un líquido genera un vapor que puede alcanzar una presión y concentración características conocidas como punto de saturación. Generalmente, los vapores del líquido están sujetos a fluctuaciones, logrando solo concentraciones y presiones parciales que pueden caracterizarse en función de su grado de saturación. Un ejemplo de esto es la humedad relativa, que representa el porcentaje de humedad presente en relación con la concentración saturada del vapor de agua.
ID:(373, 0)
Vapor de agua
Imagen 
La fase gaseosa del agua corresponde a lo que se denomina el vapor de agua. Esta se crea cuando las moléculas de agua adquieren suficiente energía cinética para escapar de la fase líquida y comienzan a moverse en el espacio sobre el líquido. Periódicamente, las moléculas en estado gaseoso chocan nuevamente contra la superficie del líquido y son capturadas, volviendo al estado líquido.
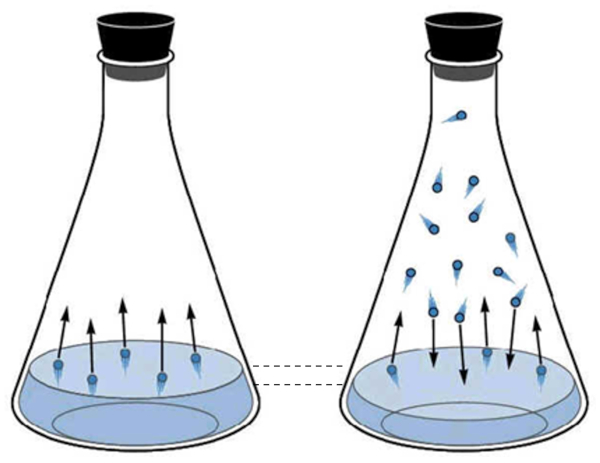
A medida que aumenta el número de moléculas en estado gaseoso, también aumenta el número de moléculas que regresan al estado líquido. Este proceso continúa hasta que se alcanza un equilibrio entre las moléculas que abandonan el líquido y las que son reabsorbidas. En esta situación, se dice que el espacio sobre el líquido está saturado.
ID:(1010, 0)
Cantidad de vapor de agua
Nota 
La variación de volumen en cambio de fase ($\Delta V$), al cambiar de fase de un líquido a un gas, se puede expresar como:
$\Delta V = V_{\text{gas}} - V_{\text{líquido}}$
Dado que el volumen del gas es significativamente mayor que el del líquido,
$V_{\text{gas}} \gg V_{\text{líquido}}$
podemos aproximar:
$\Delta V \approx V_{\text{gas}}$
Debido a que el vapor de agua exhibe un comportamiento similar al de un gas ideal, podemos afirmar que con los valores de la constante universal de los gases ($R_C$), el número de moles ($n$), la temperatura absoluta ($T$) y la presión de vapor de agua no saturado ($p_v$):
| $ p_v \Delta V = n_v R_C T $ |
por lo que la variación de volumen en cambio de fase ($\Delta V$) es
$\Delta V = \displaystyle\frac{nRT}{p_v}$
ID:(3185, 0)
Presión de vapor de agua saturado
Cita 
Utilizando la ecuación de Clausius-Clapeyron para el gradiente de la presión ($p$) en relación con la temperatura absoluta ($T$), que depende de el calor latente ($L$) y la variación de volumen en cambio de fase ($\Delta V$):
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$ |
En el caso del cambio de fase de líquido a gas, podemos suponer que el cambio de volumen es aproximadamente igual al volumen del vapor, por lo que podemos utilizar la ecuación de los gases con el número de moles ($n$), el volumen ($V$), la constante universal de los gases ($R_C$) y la presión ($p$):
| $ p V = n R_C T $ |
Dado que la ecuación de Clausius-Clapeyron se puede expresar como:
$\displaystyle\frac{dp}{dT}=\displaystyle\frac{L}{n}\displaystyle\frac{p}{R T^2}$
Donde el calor latente molar ($l_m$) ($l_m = L/n$) representa el cambio de entalpía en el cambio de fase $\Delta h$ (la energía necesaria para formar el agua), finalmente obtenemos:
$\displaystyle\frac{dp}{dT}=l_m\displaystyle\frac{p}{RT^2}$
Si integramos esta ecuación entre la presión de vapor de agua saturado ($p_s$) y la presión en el punto $p_0$ a la temperatura $T_0$, obtenemos:
$p_s=p_0e^{l_m/RT_0}e^{-l_m/RT}$
Si evaluamos esta expresión con los datos del punto crítico:
$p_{ref}=p_0e^{l_m/RT_0}$
Finalmente, tenemos:
| $ p_s = p_{ref} e^{- l_m / R_C T }$ |
ID:(15767, 0)
Humedad relativa
Ejercicio 
La relación entre la humedad relativa ($RH$) con la concentración de moleculas de vapor de agua ($c_v$) y ERROR:4952,0 se expresa como:
| $ RH =\displaystyle\frac{ c_v }{ c_s }$ |
y relacionando la presión ($p$) con la concentración molar ($c_m$), la temperatura absoluta ($T$) y la constante universal de los gases ($R_C$) se obtiene:
| $ p = c_m R_C T $ |
Esto se aplica a la presión de vapor de agua, donde:
$p_v = c_v R T$
y a la presión saturada de vapor de agua:
$p_s = c_s R T$
Lo que resulta en la siguiente ecuación:
| $ RH =\displaystyle\frac{ p_v }{ p_s }$ |
ID:(15768, 0)
Vapor
Descripción 
La evaporación de un líquido genera un vapor que puede alcanzar una presión y concentración características conocidas como punto de saturación. Generalmente, los vapores del líquido están sujetos a fluctuaciones, logrando solo concentraciones y presiones parciales que pueden caracterizarse en función de su grado de saturación. Un ejemplo de esto es la humedad relativa, que representa el porcentaje de humedad presente en relación con la concentración saturada del vapor de agua.
Variables
Cálculos
Cálculos
Ecuaciones
Utilizando la ecuaci n de Clausius-Clapeyron para el gradiente de la presión ($p$) en relaci n con la temperatura absoluta ($T$), que depende de el calor latente ($L$) y la variación de volumen en cambio de fase ($\Delta V$):
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$ |
En el caso del cambio de fase de l quido a gas, podemos suponer que el cambio de volumen es aproximadamente igual al volumen del vapor, por lo que podemos utilizar la ecuaci n de los gases con el número de moles ($n$), el volumen ($V$), la constante universal de los gases ($R_C$) y la presión de vapor de agua no saturado ($p_v$):
| $$ |
Dado que la ecuaci n de Clausius-Clapeyron se puede expresar como:
$\displaystyle\frac{dp}{dT}=\displaystyle\frac{L}{n}\displaystyle\frac{p}{R T^2}$
Donde el calor latente molar ($l_m$) ($l_m = L/n$) representa el cambio de entalp a en el cambio de fase $\Delta h$ (la energ a necesaria para formar el agua), finalmente obtenemos:
$\displaystyle\frac{dp}{dT}=l_m\displaystyle\frac{p}{RT^2}$
Si integramos esta ecuaci n entre la presión de vapor de agua saturado ($p_s$) y la presi n en el punto
$p_s=p_0e^{l_m/RT_0}e^{-l_m/RT}$
Si evaluamos esta expresi n con los datos del punto cr tico:
$p_{ref}=p_0e^{l_m/RT_0}$
Finalmente, tenemos:
| $ p_s = p_{ref} e^{- l_m / R_C T }$ |
(ID 3182)
La presión ($p$), el volumen ($V$), la temperatura absoluta ($T$) y el número de moles ($n$) est n vinculados a trav s de las siguientes leyes f sicas:
• La ley de Boyle
| $ p V = C_b $ |
• La ley de Charles
| $\displaystyle\frac{ V }{ T } = C_c$ |
• La ley de Gay-Lussac
| $\displaystyle\frac{ p }{ T } = C_g$ |
• La ley de Avogadro
| $\displaystyle\frac{ n }{ V } = C_a $ |
Estas leyes pueden ser expresadas de manera m s general como:
$\displaystyle\frac{pV}{nT}=cte$
Esta relaci n general establece que el producto de la presi n y el volumen dividido por el n mero de moles y la temperatura se mantiene constante:
| $ p V = n R_C T $ |
(ID 3183)
La presión ($p$), el volumen ($V$), la temperatura absoluta ($T$) y el número de moles ($n$) est n vinculados a trav s de las siguientes leyes f sicas:
• La ley de Boyle
| $ p V = C_b $ |
• La ley de Charles
| $\displaystyle\frac{ V }{ T } = C_c$ |
• La ley de Gay-Lussac
| $\displaystyle\frac{ p }{ T } = C_g$ |
• La ley de Avogadro
| $\displaystyle\frac{ n }{ V } = C_a $ |
Estas leyes pueden ser expresadas de manera m s general como:
$\displaystyle\frac{pV}{nT}=cte$
Esta relaci n general establece que el producto de la presi n y el volumen dividido por el n mero de moles y la temperatura se mantiene constante:
| $ p V = n R_C T $ |
(ID 3183)
(ID 3200)
La relaci n entre la humedad relativa ($RH$) con la concentración de moleculas de vapor de agua ($c_v$) y ERROR:4952,0 se expresa como:
| $ RH =\displaystyle\frac{ c_v }{ c_s }$ |
y relacionando la presión ($p$) con la concentración molar ($c_m$), la temperatura absoluta ($T$) y la constante universal de los gases ($R_C$) se obtiene:
| $ p = c_m R_C T $ |
Esto se aplica a la presi n de vapor de agua, donde:
$p_v = c_v R T$
y a la presi n saturada de vapor de agua:
$p_s = c_s R T$
Lo que resulta en la siguiente ecuaci n:
| $ RH =\displaystyle\frac{ p_v }{ p_s }$ |
(ID 4478)
Cuando la presión ($p$) se comporta como un gas ideal, cumpliendo con el volumen ($V$), el número de moles ($n$), la temperatura absoluta ($T$) y la constante universal de los gases ($R_C$), la ecuaci n de los gases:
| $ p V = n R_C T $ |
y la definici n de la concentración molar ($c_m$):
| $ c_m \equiv\displaystyle\frac{ n }{ V }$ |
llevan a la siguiente relaci n:
| $ p = c_m R_C T $ |
(ID 4479)
Cuando la presión ($p$) se comporta como un gas ideal, cumpliendo con el volumen ($V$), el número de moles ($n$), la temperatura absoluta ($T$) y la constante universal de los gases ($R_C$), la ecuaci n de los gases:
| $ p V = n R_C T $ |
y la definici n de la concentración molar ($c_m$):
| $ c_m \equiv\displaystyle\frac{ n }{ V }$ |
llevan a la siguiente relaci n:
| $ p = c_m R_C T $ |
(ID 4479)
Ejemplos
La evaporaci n ocurre cuando part culas de un l quido alcanzan su superficie y poseen suficiente energ a para escapar, transform ndose en parte del gas que denominamos vapor. Para que esto sea posible, algunas part culas deben tener la energ a necesaria para superar las fuerzas de atracci n que existen entre las mol culas del l quido. Esta energ a es principalmente energ a cin tica, por lo que su escape depende de que su velocidad supere un umbral m nimo.
(ID 15289)
La fase gaseosa del agua corresponde a lo que se denomina el vapor de agua. Esta se crea cuando las mol culas de agua adquieren suficiente energ a cin tica para escapar de la fase l quida y comienzan a moverse en el espacio sobre el l quido. Peri dicamente, las mol culas en estado gaseoso chocan nuevamente contra la superficie del l quido y son capturadas, volviendo al estado l quido.

A medida que aumenta el n mero de mol culas en estado gaseoso, tambi n aumenta el n mero de mol culas que regresan al estado l quido. Este proceso contin a hasta que se alcanza un equilibrio entre las mol culas que abandonan el l quido y las que son reabsorbidas. En esta situaci n, se dice que el espacio sobre el l quido est saturado.
(ID 1010)
La variación de volumen en cambio de fase ($\Delta V$), al cambiar de fase de un l quido a un gas, se puede expresar como:
$\Delta V = V_{\text{gas}} - V_{\text{l quido}}$
Dado que el volumen del gas es significativamente mayor que el del l quido,
$V_{\text{gas}} \gg V_{\text{l quido}}$
podemos aproximar:
$\Delta V \approx V_{\text{gas}}$
Debido a que el vapor de agua exhibe un comportamiento similar al de un gas ideal, podemos afirmar que con los valores de la constante universal de los gases ($R_C$), el número de moles ($n$), la temperatura absoluta ($T$) y la presión de vapor de agua no saturado ($p_v$):
| $ p_v \Delta V = n_v R_C T $ |
por lo que la variación de volumen en cambio de fase ($\Delta V$) es
$\Delta V = \displaystyle\frac{nRT}{p_v}$
(ID 3185)
Utilizando la ecuaci n de Clausius-Clapeyron para el gradiente de la presión ($p$) en relaci n con la temperatura absoluta ($T$), que depende de el calor latente ($L$) y la variación de volumen en cambio de fase ($\Delta V$):
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$ |
En el caso del cambio de fase de l quido a gas, podemos suponer que el cambio de volumen es aproximadamente igual al volumen del vapor, por lo que podemos utilizar la ecuaci n de los gases con el número de moles ($n$), el volumen ($V$), la constante universal de los gases ($R_C$) y la presión ($p$):
| $ p V = n R_C T $ |
Dado que la ecuaci n de Clausius-Clapeyron se puede expresar como:
$\displaystyle\frac{dp}{dT}=\displaystyle\frac{L}{n}\displaystyle\frac{p}{R T^2}$
Donde el calor latente molar ($l_m$) ($l_m = L/n$) representa el cambio de entalp a en el cambio de fase $\Delta h$ (la energ a necesaria para formar el agua), finalmente obtenemos:
$\displaystyle\frac{dp}{dT}=l_m\displaystyle\frac{p}{RT^2}$
Si integramos esta ecuaci n entre la presión de vapor de agua saturado ($p_s$) y la presi n en el punto $p_0$ a la temperatura $T_0$, obtenemos:
$p_s=p_0e^{l_m/RT_0}e^{-l_m/RT}$
Si evaluamos esta expresi n con los datos del punto cr tico:
$p_{ref}=p_0e^{l_m/RT_0}$
Finalmente, tenemos:
| $ p_s = p_{ref} e^{- l_m / R_C T }$ |
(ID 15767)
La relaci n entre la humedad relativa ($RH$) con la concentración de moleculas de vapor de agua ($c_v$) y ERROR:4952,0 se expresa como:
| $ RH =\displaystyle\frac{ c_v }{ c_s }$ |
y relacionando la presión ($p$) con la concentración molar ($c_m$), la temperatura absoluta ($T$) y la constante universal de los gases ($R_C$) se obtiene:
| $ p = c_m R_C T $ |
Esto se aplica a la presi n de vapor de agua, donde:
$p_v = c_v R T$
y a la presi n saturada de vapor de agua:
$p_s = c_s R T$
Lo que resulta en la siguiente ecuaci n:
| $ RH =\displaystyle\frac{ p_v }{ p_s }$ |
(ID 15768)
(ID 15347)
La masa evaporada ($\Delta m$) se define utilizando el calor latente ($L$) y el calor de cambio de fase ($\Delta Q$) de la siguiente manera:
| $ \Delta Q = L \Delta m$ |
(ID 3200)
En muchas ocasiones, no se dispone del calor latente molar, sino del calor latente que se expresa, por ejemplo, en Joules por kilogramo (J/kg). Dado que la ecuaci n de presi n de vapor trabaja con el calor latente molar, es necesario convertir el calor latente en calor latente molar. Como este ltimo se refiere a la cantidad por mol, simplemente dividimos el calor latente ($L$) por la masa molar ($M_m$) para obtener el calor latente molar ($l_m$):
| $ l_m \equiv\displaystyle\frac{ L }{ M_m }$ |
En el caso del agua, el calor latente de evaporaci n es del orden de $L\sim 2.256\times 10^6 J/kg$, mientras que la masa molar es $M_m\sim 18 g/cm^3 = 0.018 kg/m^3$. De esta manera, obtenemos un calor latente molar de $L_m\sim 40600 J/mol = 40.6 kJ/mol$.
(ID 9273)
La variaci n del volumen entre el material en dos estados distintos puede expresarse en moles
| $\Delta v_m =\displaystyle\frac{ \Delta V }{ M_m }$ |
para obtener un indicador caracter stico del material.
(ID 12823)
La presión de vapor de agua saturado ($p_s$) se puede calcular utilizando la presión de referencia ($p_{ref}$), la constante universal de los gases ($R_C$), la temperatura absoluta ($T$) y el calor latente molar ($l_m$) de acuerdo con la siguiente f rmula:
| $ p_s = p_{ref} e^{- l_m / R_C T }$ |
(ID 3182)
La presión ($p$), el volumen ($V$), la temperatura absoluta ($T$), y el número de moles ($n$) est n relacionados por la siguiente ecuaci n:
| $ p V = n R_C T $ |
donde la constante universal de los gases ($R_C$) tiene el valor de 8.314 J/K mol.
(ID 3183)
La presión ($p$), el volumen ($V$), la temperatura absoluta ($T$), y el número de moles ($n$) est n relacionados por la siguiente ecuaci n:
| $ p V = n R_C T $ |
donde la constante universal de los gases ($R_C$) tiene el valor de 8.314 J/K mol.
(ID 3183)
La humedad relativa ($RH$) se puede expresar en t rminos de la presión de vapor de agua no saturado ($p_v$) y la presión de vapor de agua saturado ($p_s$) de la siguiente manera:
| $ RH =\displaystyle\frac{ p_v }{ p_s }$ |
(ID 4478)
La presión ($p$) se puede calcular a partir de la concentración molar ($c_m$) utilizando la temperatura absoluta ($T$) y la constante universal de los gases ($R_C$) de la siguiente manera:
| $ p = c_m R_C T $ |
(ID 4479)
La presión ($p$) se puede calcular a partir de la concentración molar ($c_m$) utilizando la temperatura absoluta ($T$) y la constante universal de los gases ($R_C$) de la siguiente manera:
| $ p = c_m R_C T $ |
(ID 4479)
La relaci n entre la concentración de moleculas de vapor de agua ($c_v$) y ERROR:4952,0 se llama la humedad relativa ($RH$). En otras palabras, cuando se alcanza una humedad relativa del 100%, la concentraci n existente ser igual a la concentraci n saturada.
| $ RH =\displaystyle\frac{ c_v }{ c_s }$ |
(ID 3175)
ID:(373, 0)
