Wasserdampf
Storyboard 
Die Verdampfung einer Flüssigkeit erzeugt einen Dampf, der einen charakteristischen Druck und eine charakteristische Konzentration erreichen kann, die als Sättigungspunkt bezeichnet werden. Typischerweise unterliegen die Dämpfe der Flüssigkeit Schwankungen und erreichen nur partielle Konzentrationen und Drücke, die anhand ihres Sättigungsgrades charakterisiert werden können. Ein Beispiel dafür ist die relative Luftfeuchtigkeit, die den Prozentsatz der vorhandenen Feuchtigkeit im Verhältnis zur gesättigten Konzentration des Wasserdampfs darstellt.
ID:(373, 0)
Wasserdampf
Bild 
Die gasförmige Phase des Wassers entspricht dem, was als Wasserdampf bekannt ist. Diese entsteht, wenn Wassermoleküle genügend kinetische Energie erhalten, um aus der flüssigen Phase zu entweichen und sich im Raum über der Flüssigkeit zu bewegen. Periodisch kollidieren die Moleküle im gasförmigen Zustand erneut mit der Oberfläche der Flüssigkeit und werden erfasst, kehren in den flüssigen Zustand zurück.
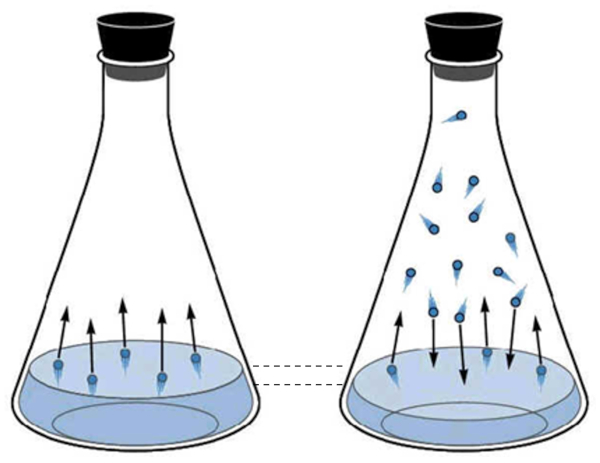
Mit zunehmender Anzahl von Molekülen im gasförmigen Zustand steigt auch die Anzahl derer, die in den flüssigen Zustand zurückkehren. Dieser Prozess setzt sich fort, bis ein Gleichgewicht zwischen den Molekülen erreicht ist, die die Flüssigkeit verlassen, und denen, die wieder aufgenommen werden. In dieser Situation wird gesagt, dass der Raum über der Flüssigkeit gesättigt ist.
ID:(1010, 0)
Menge an Wasserdampf
Notiz 
Wenn die Volumenvariation beim Phasenwechsel ($\Delta V$) von einer Flüssigkeit zu einem Gas wechselt, kann es wie folgt ausgedrückt werden:
$\Delta V = V_{\text{Gas}} - V_{\text{Flüssigkeit}}$
Da das Volumen des Gases deutlich größer ist als das der Flüssigkeit,
$V_{\text{Gas}} \gg V_{\text{Flüssigkeit}}$
können wir näherungsweise annehmen:
$\Delta V \approx V_{\text{Gas}}$
Da Wasserdampf sich ähnlich wie ein ideales Gas verhält, können wir mit den Werten von die Universelle Gas Konstante ($R_C$), der Anzahl der Mol ($n$), die Absolute Temperatur ($T$) und die Wasserdampfdruck Ungesättigte ($p_v$) sagen:
| $ p_v \Delta V = n_v R_C T $ |
Daher ist die Volumenvariation beim Phasenwechsel ($\Delta V$):
$\Delta V = \displaystyle\frac{nRT}{p_v}$
ID:(3185, 0)
Druck gesättigtem Wasserdampf
Zitat 
Unter Verwendung der Clausius-Clapeyron-Gleichung für den Gradienten von die Druck ($p$) in Bezug auf die Absolute Temperatur ($T$), der von der Latentwärme ($L$) und die Volumenvariation beim Phasenwechsel ($\Delta V$) abhängt:
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$ |
Im Fall des Phasenübergangs von Flüssigkeit zu Gas können wir annehmen, dass die Änderung des Volumens ungefähr gleich dem Volumen des Dampfes ist. Daher können wir die ideale Gasgleichung mit der Anzahl der Mol ($n$), der Volumen ($V$), die Universelle Gas Konstante ($R_C$) und die Druck ($p$) verwenden:
| $ p V = n R_C T $ |
Da die Clausius-Clapeyron-Gleichung wie folgt geschrieben werden kann:
$\displaystyle\frac{dp}{dT}=\displaystyle\frac{L}{n}\displaystyle\frac{p}{R T^2}$
Wobei der Molare Latenzwärme ($l_m$) ($l_m = L/n$) der Änderung der Enthalpie während des Phasenübergangs h entspricht (die für die Bildung von Wasser benötigte Energie), erhalten wir schließlich:
$\displaystyle\frac{dp}{dT}=l_m\displaystyle\frac{p}{RT^2}$
Wenn wir diese Gleichung zwischen die Druck gesättigtem Wasserdampf ($p_s$) und dem Druck am Punkt
$p_s=p_0e^{l_m/RT_0}e^{-l_m/RT}$
Wenn wir diesen Ausdruck mit den Daten am kritischen Punkt auswerten:
$p_{ref}=p_0e^{l_m/RT_0}$
Haben wir schließlich:
| $ p_s = p_{ref} e^{- l_m / R_C T }$ |
ID:(15767, 0)
Presión Vapor de Agua
Übung 
Die Beziehung zwischen die Relative Luftfeuchtigkeit ($RH$) mit die Konzentration von Wasserdampfmolekülen ($c_v$) und ERROR:4952,0 wird wie folgt ausgedrückt:
| $ RH =\displaystyle\frac{ c_v }{ c_s }$ |
und durch die Beziehung zwischen die Druck ($p$) mit die Molare Konzentration ($c_m$), die Absolute Temperatur ($T$) und die Universelle Gas Konstante ($R_C$) erhalten wir:
| $ p = c_m R_C T $ |
Dies gilt für den Wasserdampfdruck, wobei:
$p_v = c_v R T$
und den gesättigten Wasserdampfdruck:
$p_s = c_s R T$
was zur folgenden Gleichung führt:
| $ RH =\displaystyle\frac{ p_v }{ p_s }$ |
ID:(15768, 0)
Dampf
Beschreibung 
Die Verdampfung einer Flüssigkeit erzeugt einen Dampf, der einen charakteristischen Druck und eine charakteristische Konzentration erreichen kann, die als Sättigungspunkt bezeichnet werden. Typischerweise unterliegen die Dämpfe der Flüssigkeit Schwankungen und erreichen nur partielle Konzentrationen und Drücke, die anhand ihres Sättigungsgrades charakterisiert werden können. Ein Beispiel dafür ist die relative Luftfeuchtigkeit, die den Prozentsatz der vorhandenen Feuchtigkeit im Verhältnis zur gesättigten Konzentration des Wasserdampfs darstellt.
Variablen
Berechnungen
Berechnungen
Gleichungen
Unter Verwendung der Clausius-Clapeyron-Gleichung f r den Gradienten von die Druck ($p$) in Bezug auf die Absolute Temperatur ($T$), der von der Latentwärme ($L$) und die Volumenvariation beim Phasenwechsel ($\Delta V$) abh ngt:
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$ |
Im Fall des Phasen bergangs von Fl ssigkeit zu Gas k nnen wir annehmen, dass die nderung des Volumens ungef hr gleich dem Volumen des Dampfes ist. Daher k nnen wir die ideale Gasgleichung mit der Anzahl der Mol ($n$), der Volumen ($V$), die Universelle Gas Konstante ($R_C$) und die Wasserdampfdruck Ungesättigte ($p_v$) verwenden:
| $$ |
Da die Clausius-Clapeyron-Gleichung wie folgt geschrieben werden kann:
$\displaystyle\frac{dp}{dT}=\displaystyle\frac{L}{n}\displaystyle\frac{p}{R T^2}$
Wobei der Molare Latenzwärme ($l_m$) ($l_m = L/n$) der nderung der Enthalpie w hrend des Phasen bergangs h entspricht (die f r die Bildung von Wasser ben tigte Energie), erhalten wir schlie lich:
$\displaystyle\frac{dp}{dT}=l_m\displaystyle\frac{p}{RT^2}$
Wenn wir diese Gleichung zwischen die Druck gesättigtem Wasserdampf ($p_s$) und dem Druck am Punkt
$p_s=p_0e^{l_m/RT_0}e^{-l_m/RT}$
Wenn wir diesen Ausdruck mit den Daten am kritischen Punkt auswerten:
$p_{ref}=p_0e^{l_m/RT_0}$
Haben wir schlie lich:
| $ p_s = p_{ref} e^{- l_m / R_C T }$ |
(ID 3182)
Die Druck ($p$), der Volumen ($V$), die Absolute Temperatur ($T$) und der Anzahl der Mol ($n$) stehen im Zusammenhang mit den folgenden physikalischen Gesetzen:
• Das Gesetz von Boyle
| $ p V = C_b $ |
• Das Gesetz von Charles
| $\displaystyle\frac{ V }{ T } = C_c$ |
• Das Gesetz von Gay-Lussac
| $\displaystyle\frac{ p }{ T } = C_g$ |
• Das Gesetz von Avogadro
| $\displaystyle\frac{ n }{ V } = C_a $ |
Diese Gesetze k nnen in einer allgemeineren Form ausgedr ckt werden:
$\displaystyle\frac{pV}{nT}=cte$
Diese allgemeine Beziehung besagt, dass das Produkt aus Druck und Volumen durch die Anzahl der Mol und die Temperatur geteilt konstant bleibt:
| $ p V = n R_C T $ |
(ID 3183)
Die Druck ($p$), der Volumen ($V$), die Absolute Temperatur ($T$) und der Anzahl der Mol ($n$) stehen im Zusammenhang mit den folgenden physikalischen Gesetzen:
• Das Gesetz von Boyle
| $ p V = C_b $ |
• Das Gesetz von Charles
| $\displaystyle\frac{ V }{ T } = C_c$ |
• Das Gesetz von Gay-Lussac
| $\displaystyle\frac{ p }{ T } = C_g$ |
• Das Gesetz von Avogadro
| $\displaystyle\frac{ n }{ V } = C_a $ |
Diese Gesetze k nnen in einer allgemeineren Form ausgedr ckt werden:
$\displaystyle\frac{pV}{nT}=cte$
Diese allgemeine Beziehung besagt, dass das Produkt aus Druck und Volumen durch die Anzahl der Mol und die Temperatur geteilt konstant bleibt:
| $ p V = n R_C T $ |
(ID 3183)
(ID 3200)
Die Beziehung zwischen die Relative Luftfeuchtigkeit ($RH$) mit die Konzentration von Wasserdampfmolekülen ($c_v$) und ERROR:4952,0 wird wie folgt ausgedr ckt:
| $ RH =\displaystyle\frac{ c_v }{ c_s }$ |
und durch die Beziehung zwischen die Druck ($p$) mit die Molare Konzentration ($c_m$), die Absolute Temperatur ($T$) und die Universelle Gas Konstante ($R_C$) erhalten wir:
| $ p = c_m R_C T $ |
Dies gilt f r den Wasserdampfdruck, wobei:
$p_v = c_v R T$
und den ges ttigten Wasserdampfdruck:
$p_s = c_s R T$
was zur folgenden Gleichung f hrt:
| $ RH =\displaystyle\frac{ p_v }{ p_s }$ |
(ID 4478)
Wenn die Druck ($p$) sich wie ein ideales Gas verh lt und der Volumen ($V$), der Anzahl der Mol ($n$), die Absolute Temperatur ($T$) und die Universelle Gas Konstante ($R_C$) erf llt, f hrt die ideale Gasgleichung:
| $ p V = n R_C T $ |
und die Definition von die Molare Konzentration ($c_m$):
| $ c_m \equiv\displaystyle\frac{ n }{ V }$ |
zu folgender Beziehung:
| $ p = c_m R_C T $ |
(ID 4479)
Wenn die Druck ($p$) sich wie ein ideales Gas verh lt und der Volumen ($V$), der Anzahl der Mol ($n$), die Absolute Temperatur ($T$) und die Universelle Gas Konstante ($R_C$) erf llt, f hrt die ideale Gasgleichung:
| $ p V = n R_C T $ |
und die Definition von die Molare Konzentration ($c_m$):
| $ c_m \equiv\displaystyle\frac{ n }{ V }$ |
zu folgender Beziehung:
| $ p = c_m R_C T $ |
(ID 4479)
Beispiele
Verdunstung tritt auf, wenn Teilchen in einer Fl ssigkeit die Oberfl che erreichen und gen gend Energie besitzen, um zu entweichen und Teil des Gases zu werden, das wir als Dampf bezeichnen. Damit dies geschieht, m ssen einige Teilchen genug Energie haben, um die Anziehungskr fte zwischen den Molek len der Fl ssigkeit zu berwinden. Diese Energie ist haupts chlich kinetischer Natur, sodass das Entweichen von einer Mindestgeschwindigkeit abh ngt.
(ID 15289)
Die gasf rmige Phase des Wassers entspricht dem, was als Wasserdampf bekannt ist. Diese entsteht, wenn Wassermolek le gen gend kinetische Energie erhalten, um aus der fl ssigen Phase zu entweichen und sich im Raum ber der Fl ssigkeit zu bewegen. Periodisch kollidieren die Molek le im gasf rmigen Zustand erneut mit der Oberfl che der Fl ssigkeit und werden erfasst, kehren in den fl ssigen Zustand zur ck.

Mit zunehmender Anzahl von Molek len im gasf rmigen Zustand steigt auch die Anzahl derer, die in den fl ssigen Zustand zur ckkehren. Dieser Prozess setzt sich fort, bis ein Gleichgewicht zwischen den Molek len erreicht ist, die die Fl ssigkeit verlassen, und denen, die wieder aufgenommen werden. In dieser Situation wird gesagt, dass der Raum ber der Fl ssigkeit ges ttigt ist.
(ID 1010)
Wenn die Volumenvariation beim Phasenwechsel ($\Delta V$) von einer Fl ssigkeit zu einem Gas wechselt, kann es wie folgt ausgedr ckt werden:
$\Delta V = V_{\text{Gas}} - V_{\text{Fl ssigkeit}}$
Da das Volumen des Gases deutlich gr er ist als das der Fl ssigkeit,
$V_{\text{Gas}} \gg V_{\text{Fl ssigkeit}}$
k nnen wir n herungsweise annehmen:
$\Delta V \approx V_{\text{Gas}}$
Da Wasserdampf sich hnlich wie ein ideales Gas verh lt, k nnen wir mit den Werten von die Universelle Gas Konstante ($R_C$), der Anzahl der Mol ($n$), die Absolute Temperatur ($T$) und die Wasserdampfdruck Ungesättigte ($p_v$) sagen:
| $ p_v \Delta V = n_v R_C T $ |
Daher ist die Volumenvariation beim Phasenwechsel ($\Delta V$):
$\Delta V = \displaystyle\frac{nRT}{p_v}$
(ID 3185)
Unter Verwendung der Clausius-Clapeyron-Gleichung f r den Gradienten von die Druck ($p$) in Bezug auf die Absolute Temperatur ($T$), der von der Latentwärme ($L$) und die Volumenvariation beim Phasenwechsel ($\Delta V$) abh ngt:
| $\displaystyle\frac{ dp }{ dT }=\displaystyle\frac{ L }{ \Delta V T }$ |
Im Fall des Phasen bergangs von Fl ssigkeit zu Gas k nnen wir annehmen, dass die nderung des Volumens ungef hr gleich dem Volumen des Dampfes ist. Daher k nnen wir die ideale Gasgleichung mit der Anzahl der Mol ($n$), der Volumen ($V$), die Universelle Gas Konstante ($R_C$) und die Druck ($p$) verwenden:
| $ p V = n R_C T $ |
Da die Clausius-Clapeyron-Gleichung wie folgt geschrieben werden kann:
$\displaystyle\frac{dp}{dT}=\displaystyle\frac{L}{n}\displaystyle\frac{p}{R T^2}$
Wobei der Molare Latenzwärme ($l_m$) ($l_m = L/n$) der nderung der Enthalpie w hrend des Phasen bergangs h entspricht (die f r die Bildung von Wasser ben tigte Energie), erhalten wir schlie lich:
$\displaystyle\frac{dp}{dT}=l_m\displaystyle\frac{p}{RT^2}$
Wenn wir diese Gleichung zwischen die Druck gesättigtem Wasserdampf ($p_s$) und dem Druck am Punkt
$p_s=p_0e^{l_m/RT_0}e^{-l_m/RT}$
Wenn wir diesen Ausdruck mit den Daten am kritischen Punkt auswerten:
$p_{ref}=p_0e^{l_m/RT_0}$
Haben wir schlie lich:
| $ p_s = p_{ref} e^{- l_m / R_C T }$ |
(ID 15767)
Die Beziehung zwischen die Relative Luftfeuchtigkeit ($RH$) mit die Konzentration von Wasserdampfmolekülen ($c_v$) und ERROR:4952,0 wird wie folgt ausgedr ckt:
| $ RH =\displaystyle\frac{ c_v }{ c_s }$ |
und durch die Beziehung zwischen die Druck ($p$) mit die Molare Konzentration ($c_m$), die Absolute Temperatur ($T$) und die Universelle Gas Konstante ($R_C$) erhalten wir:
| $ p = c_m R_C T $ |
Dies gilt f r den Wasserdampfdruck, wobei:
$p_v = c_v R T$
und den ges ttigten Wasserdampfdruck:
$p_s = c_s R T$
was zur folgenden Gleichung f hrt:
| $ RH =\displaystyle\frac{ p_v }{ p_s }$ |
(ID 15768)
(ID 15347)
Die Evaporated Messe ($\Delta m$) wird unter Verwendung von der Latentwärme ($L$) und der Phasenwechsel Wärme ($\Delta Q$) wie folgt definiert:
| $ \Delta Q = L \Delta m$ |
(ID 3200)
In vielen F llen steht nicht die latente molare W rme zur Verf gung, sondern die latente W rme, die beispielsweise in Joule pro Kilogramm (J / kg) ausgedr ckt wird. Da die Dampfdruckgleichung mit der latenten molaren W rme funktioniert, m ssen wir die latente W rme in latente molare W rme umwandeln. Da letzteres pro Mol ist, reicht es aus, die latente W rme
| $ l_m \equiv\displaystyle\frac{ L }{ M_m }$ |
Im Fall von Wasser liegt die latente Verdampfungsw rme in der Gr enordnung von
(ID 9273)
Die nderung des Volumens zwischen dem Material in zwei verschiedenen Zust nden kann in Mol ausgedr ckt werden
| $\Delta v_m =\displaystyle\frac{ \Delta V }{ M_m }$ |
um einen charakteristischen Indikator f r das Material zu erhalten.
(ID 12823)
Die Druck gesättigtem Wasserdampf ($p_s$) kann mit die Referenzdruck ($p_{ref}$), die Universelle Gas Konstante ($R_C$), die Absolute Temperatur ($T$) und der Molare Latenzwärme ($l_m$) entsprechend berechnet werden folgende Formel:
| $ p_s = p_{ref} e^{- l_m / R_C T }$ |
(ID 3182)
Die Druck ($p$), der Volumen ($V$), die Absolute Temperatur ($T$) und der Anzahl der Mol ($n$) sind durch die folgende Gleichung verbunden:
| $ p V = n R_C T $ |
wobei die Universelle Gas Konstante ($R_C$) einen Wert von 8,314 J/K mol hat.
(ID 3183)
Die Druck ($p$), der Volumen ($V$), die Absolute Temperatur ($T$) und der Anzahl der Mol ($n$) sind durch die folgende Gleichung verbunden:
| $ p V = n R_C T $ |
wobei die Universelle Gas Konstante ($R_C$) einen Wert von 8,314 J/K mol hat.
(ID 3183)
Die Relative Luftfeuchtigkeit ($RH$) kann in Form von die Wasserdampfdruck Ungesättigte ($p_v$) und die Druck gesättigtem Wasserdampf ($p_s$) wie folgt ausgedr ckt werden:
| $ RH =\displaystyle\frac{ p_v }{ p_s }$ |
(ID 4478)
Die Druck ($p$) kann aus die Molare Konzentration ($c_m$) unter Verwendung von die Absolute Temperatur ($T$) und die Universelle Gas Konstante ($R_C$) wie folgt berechnet werden:
| $ p = c_m R_C T $ |
(ID 4479)
Die Druck ($p$) kann aus die Molare Konzentration ($c_m$) unter Verwendung von die Absolute Temperatur ($T$) und die Universelle Gas Konstante ($R_C$) wie folgt berechnet werden:
| $ p = c_m R_C T $ |
(ID 4479)
Die Beziehung zwischen die Konzentration von Wasserdampfmolekülen ($c_v$) und ERROR:4952,0 wird als die Relative Luftfeuchtigkeit ($RH$) bezeichnet. Mit anderen Worten, wenn eine relative Luftfeuchtigkeit von 100% erreicht wird, wird die vorhandene Konzentration gleich der ges ttigten Konzentration sein.
| $ RH =\displaystyle\frac{ c_v }{ c_s }$ |
(ID 3175)
ID:(373, 0)
