Gleichgewichtszustand und Temperatur
Storyboard 
Um Systeme mit Hilfe der statistischen Mechanik zu modellieren, müssen wir untersuchen, wie die Parameter, die das makroskopische System beschreiben, die statistischen Ensembles beeinflussen können. Im Falle von Teilchen wird die Temperatur als Parameter festgelegt, der zeigt, ob die Systeme im Gleichgewicht sind und ihre Energien auf einem konstanten Niveau halten
ID:(436, 0)
Ein System in Kontakt mit einem Reservoir
Definition 
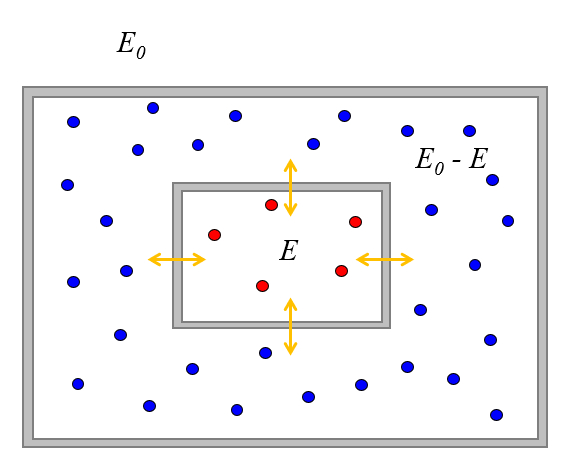
Wir können untersuchen, was passiert, wenn wir zwei Systeme von Teilchen in Kontakt bringen, so dass sie Energie, aber keine Teilchen austauschen können.
Angenommen, das System ist von seiner Umgebung isoliert, was bedeutet, dass es eine Gesamtenergie von $E_0$ hat.
Angenommen, zunächst hat das erste System eine Energie von $E$, die mit $\Omega(E)$ Zuständen verbunden ist.
Da die Gesamtenergie $E_0$ beträgt, kann das zweite System nur die Energie $E_0-E$ und eine Anzahl von verbundenen Zuständen $\Omega(E_0-E)$ haben.
Sobald wir sie in Kontakt bringen, können sie Energie austauschen, bis sie ein Gleichgewicht erreichen. In dieser Hinsicht wird der Wert von $E$ variieren, und die Wahrscheinlichkeit, die Systeme so zu finden, dass das erste einen Wert von $E$ hat, wird ebenfalls variieren.
ID:(11541, 0)
Vergleich der Anzahl der Zustandskurven
Bild 
Wenn wir betrachten, wie sich die Anzahl der Zustände mit der Energie $E$ ändert, bemerken wir, dass sich das Verhalten des Systems und des Reservoirs entgegengesetzt verhält:
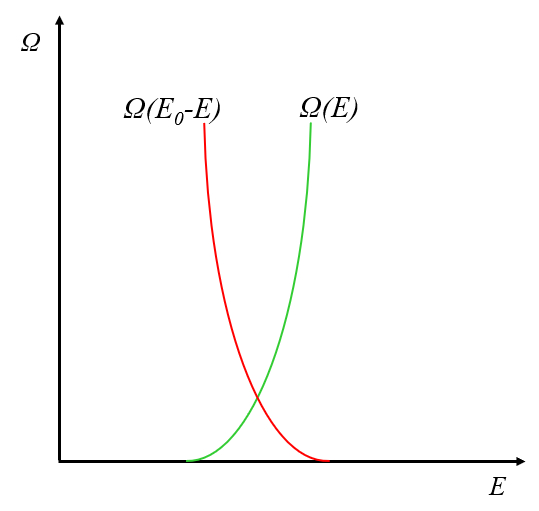
Dies geschieht, weil mit steigender Energie die Energie des Reservoirs abnimmt, was wiederum die Anzahl der erreichbaren Zustände reduziert.
ID:(11542, 0)
Bilden eines Maximums
Notiz 
Wenn wir die Anzahl der Fälle multiplizieren, erhalten wir eine Funktion mit einem sehr ausgeprägten Maximum.

Das System wird mit größerer Wahrscheinlichkeit bei der Energie gefunden, an der das Maximum der Wahrscheinlichkeitskurve auftritt.
ID:(11543, 0)
Gleichgewichtszustand und Temperatur
Beschreibung 
Um Systeme mit Hilfe der statistischen Mechanik zu modellieren, müssen wir untersuchen, wie die Parameter, die das makroskopische System beschreiben, die statistischen Ensembles beeinflussen können. Im Falle von Teilchen wird die Temperatur als Parameter festgelegt, der zeigt, ob die Systeme im Gleichgewicht sind und ihre Energien auf einem konstanten Niveau halten
Variablen
Berechnungen
Berechnungen
Gleichungen
(ID 3438)
Beispiele
Wir k nnen untersuchen, was passiert, wenn wir zwei Systeme von Teilchen in Kontakt bringen, so dass sie Energie, aber keine Teilchen austauschen k nnen.
Angenommen, das System ist von seiner Umgebung isoliert, was bedeutet, dass es eine Gesamtenergie von $E_0$ hat.
Angenommen, zun chst hat das erste System eine Energie von $E$, die mit $\Omega(E)$ Zust nden verbunden ist.
Da die Gesamtenergie $E_0$ betr gt, kann das zweite System nur die Energie $E_0-E$ und eine Anzahl von verbundenen Zust nden $\Omega(E_0-E)$ haben.
Sobald wir sie in Kontakt bringen, k nnen sie Energie austauschen, bis sie ein Gleichgewicht erreichen. In dieser Hinsicht wird der Wert von $E$ variieren, und die Wahrscheinlichkeit, die Systeme so zu finden, dass das erste einen Wert von $E$ hat, wird ebenfalls variieren.

(ID 11541)
Jedes System $\Omega$ hat eine Anzahl m glicher Zust nde, die von seiner Energie $E$ abh ngt. Daher wird, wenn das von uns untersuchte System eine Energie $E$ hat, die Anzahl der m glichen Zust nde als $\Omega(E)$ bezeichnet.
Das zu untersuchende System steht in Kontakt mit einem Reservoir, das Energie $E$ liefert. Die Gesamtenergie ist daher $E_0$ abz glich der Energie des eingetauchten Systems, $E$. Das Reservoir hat daher $\Omega(E_0 - E)$ m gliche Zust nde. Die Wahrscheinlichkeit, das Gesamtsystem mit einer Energie von $E$ im eingetauchten System zu finden, wird als Produkt der Anzahl der Zust nde mit ausgedr ckt:
| $P(E)=C\Omega(E)\Omega(E_0-E)$ |
wobei $C$ eine Normalisierungskonstante ist. Die Energie $E$ wird diejenige sein, f r die die Wahrscheinlichkeit maximal ist.
(ID 3434)
Wenn wir betrachten, wie sich die Anzahl der Zust nde mit der Energie $E$ ndert, bemerken wir, dass sich das Verhalten des Systems und des Reservoirs entgegengesetzt verh lt:

Dies geschieht, weil mit steigender Energie die Energie des Reservoirs abnimmt, was wiederum die Anzahl der erreichbaren Zust nde reduziert.
(ID 11542)
Wenn wir die Anzahl der F lle multiplizieren, erhalten wir eine Funktion mit einem sehr ausgepr gten Maximum.

Das System wird mit gr erer Wahrscheinlichkeit bei der Energie gefunden, an der das Maximum der Wahrscheinlichkeitskurve auftritt.
(ID 11543)
Wenn die Wahrscheinlichkeit, dass zwei isolierte Systeme, von denen jedes eine Gesamtenergie von $E_0$ hat und eines der Systeme eine Energie von $E$ hat, gegeben ist durch
| $P(E)=C\Omega(E)\Omega(E_0-E)$ |
K nnen wir die wahrscheinliche Energie $E$ sch tzen, bei der sie gefunden werden, indem wir nach der Energie $E$ ableiten und die Ableitung auf null setzen.
$\displaystyle\frac{\partial P}{\partial E}=\displaystyle\frac{\partial\Omega}{\partial E}\Omega'+\Omega\displaystyle\frac{\partial\Omega'}{\partial E}=0$
Wenn wir den Ausdruck durch $\Omega\Omega'$ teilen und die Energie-Differenz $E_0-E$ durch $E'$ ersetzen, k nnen wir die Bedingung zur Bestimmung der wahrscheinlichsten Situation wie folgt umformulieren:
Wenn es eine Wahrscheinlichkeit $P(E)$ gibt, zu finden
$\displaystyle\frac{1}{\Omega}\displaystyle\frac{\partial\Omega}{\partial E}-\displaystyle\frac{1}{\Omega'}\displaystyle\frac{\partial\Omega'}{\partial E'}=0$
Das negative Vorzeichen ergibt sich aus der Variablen nderung, da mit
$E'=E_0-E$
die Ableitung nach $E'$ mit ergibt:
| $\displaystyle\frac{1}{\Omega}\displaystyle\frac{\partial\Omega}{\partial E}-\displaystyle\frac{1}{\Omega_h}\displaystyle\frac{\partial\Omega_h}{\partial E_h}=0$ |
(ID 4806)
Wenn ein System mit einem Energierevier $E_0$ in Kontakt steht, ist es wahrscheinlich, es mit einer Energie $E$ zu finden, f r die die Wahrscheinlichkeit mit factor de normalización $-$, numero de estados del reservorio con energía $E_0-E$ $-$, numero de estados del sistema con la energía $E$ $-$ und probabilidad del sistema de tener una energía $E$ $-$
| $P(E)=C\Omega(E)\Omega(E_0-E)$ |
ihr Maximum erreicht. Die Energie kann bestimmt werden, indem man den Ausdruck nach der Energie $E$ ableitet und auf null setzt. Dies entspricht dem Ableiten des nat rlichen Logarithmus der Wahrscheinlichkeit:
$\ln P(E) = \ln C + \ln\Omega(E) + \ln\Omega(E_0-E)$
Was zu f hrt:
$\displaystyle\frac{\partial\ln\Omega}{\partial E} + \displaystyle\frac{\partial\ln\Omega}{\partial E} = 0$
Wenn wir eine Variable ndern:
$E' = E_0 - E$
Erhalten wir die Gleichgewichtsbedingung mit factor de normalización $-$, numero de estados del reservorio con energía $E_0-E$ $-$, numero de estados del sistema con la energía $E$ $-$ und probabilidad del sistema de tener una energía $E$ $-$:
| $\displaystyle\frac{\partial\ln\Omega}{\partial E}-\displaystyle\frac{\partial\ln\Omega_h}{\partial E_h}=0$ |
(ID 3441)
Die Gleichgewichtsbedingung eines Systems in Kontakt mit einem Reservoir wird mit energía del reservorio $J$, energía del sistema $J$, numero de estados del reservorio con energía $E'$ $-$ und numero de estados del sistema con la energía $E$ $-$ ausgedr ckt:
| $\displaystyle\frac{\partial\ln\Omega}{\partial E}-\displaystyle\frac{\partial\ln\Omega_h}{\partial E_h}=0$ |
Dies erm glicht uns, eine Funktion $\beta$ mit energía del reservorio $J$, energía del sistema $J$, numero de estados del reservorio con energía $E'$ $-$ und numero de estados del sistema con la energía $E$ $-$ auf folgende Weise einzuf hren:
| $\beta(E)\equiv\displaystyle\frac{\partial\ln\Omega}{\partial E}$ |
Diese Funktion charakterisiert den Zustand des Systems und wird relevant, wenn das System im Gleichgewicht mit einem anderen System ist.
(ID 3435)
Wenn ein System mit einem Energie-Reservoir $E_0$ in Kontakt steht, ist es wahrscheinlich, es mit einer Energie $E$ zu finden, f r die mit die Wahrscheinlichkeit
| $P(E)=C\Omega(E)\Omega(E_0-E)$ |
ihr Maximum erreicht. Die Energie kann bestimmt werden, indem man den Ausdruck nach der Energie $E$ ableitet und auf null setzt. Dies entspricht dem Ableiten des nat rlichen Logarithmus der Wahrscheinlichkeit:
$\ln P(E) = \ln C + \ln\Omega(E) + \ln\Omega(E_0-E)$
Daher erhalten wir mit :
| $\displaystyle\frac{\partial\ln\Omega}{\partial E}-\displaystyle\frac{\partial\ln\Omega_h}{\partial E_h}=0$ |
Wenn wir eine Variablentransformation durchf hren
$E' = E_0 - E$
erhalten wir die Gleichgewichtsbedingung mit :
| $\beta(E)=\beta(E_h)$ |
.
(ID 3436)
Wenn wir annehmen, dass wir das System bei der Energie finden, bei der die Wahrscheinlichkeit maximal ist, k nnen wir dies mit der Gleichgewichtssituation eines Systems in Verbindung bringen, bei dem die Wahrscheinlichkeit maximal ist.
Andererseits wissen wir, dass zwei Systeme im thermischen Gleichgewicht sind, wenn ihre Temperaturen gleich sind. Daher legt die Tatsache, dass die Funktionen $\beta$ gleich sind, nahe, dass $\beta$ mit der Temperatur in Zusammenhang steht.
Da die Einheiten von $\beta$ das Reziprok der Energie sind, k nnen wir es wie folgt mit definieren:
| $ k_B T \equiv\displaystyle\frac{1}{ \beta }$ |
(ID 3437)
Durch die Einf hrung der Beziehung mit beta del reservorio $1/J$, constante de Boltzmann $J/K$ und temperatura del sistema $K$
| $ k_B T \equiv\displaystyle\frac{1}{ \beta }$ |
wird die Gleichgewichtsbedingung mit beta del reservorio $1/J$ und beta del sistema $1/J$
| $\beta(E)=\beta(E_h)$ |
auf einfach
| $ T = T_h $ |
vereinfacht.
(ID 3438)
ID:(436, 0)
