Condição e temperatura de equilíbrio
Storyboard 
Para modelar sistemas usando a mecânica estatística, é necessário investigar como os parâmetros que descrevem o sistema macroscópico podem influenciar os conjuntos estatísticos. No caso de partículas, a temperatura é estabelecida como um parâmetro que reflete se os sistemas estão em equilíbrio, mantendo suas energias em um nível constante.
ID:(436, 0)
Um sistema em contato com um reservatório
Definição 
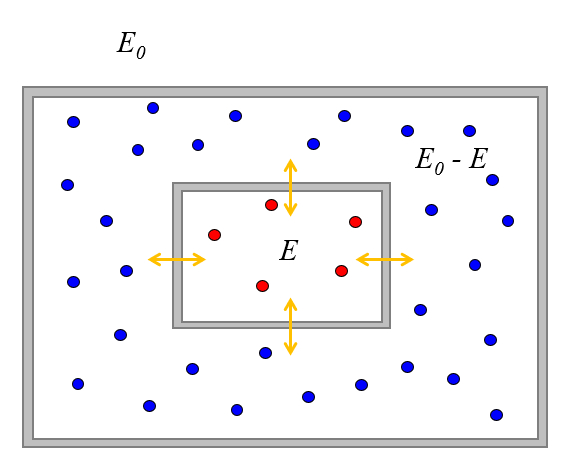
Podemos estudar o que acontece quando colocamos dois sistemas de partículas em contato, de modo que possam trocar energia, mas não partículas.
Vamos também supor que o sistema está isolado do ambiente, o que significa que possui uma energia total de $E_0$.
Suponhamos que inicialmente o primeiro sistema tenha uma energia de $E$, o que está associado a $\Omega(E)$ estados.
Uma vez que a energia total é $E_0$, o segundo sistema só pode ter energia $E_0-E$ e um número de estados associados $\Omega(E_0-E)$.
Quando os colocamos em contato, eles podem trocar energia até atingir algum equilíbrio. Nesse sentido, o valor de $E$ vai variar, e a probabilidade de encontrar os sistemas de modo que o primeiro tenha um valor de $E$ também vai variar.
ID:(11541, 0)
Comparando as curvas de número de estados
Imagem 
Quando comparamos como o número de estados varia com a energia $E$, observamos que o comportamento do sistema e do reservatório é oposto:
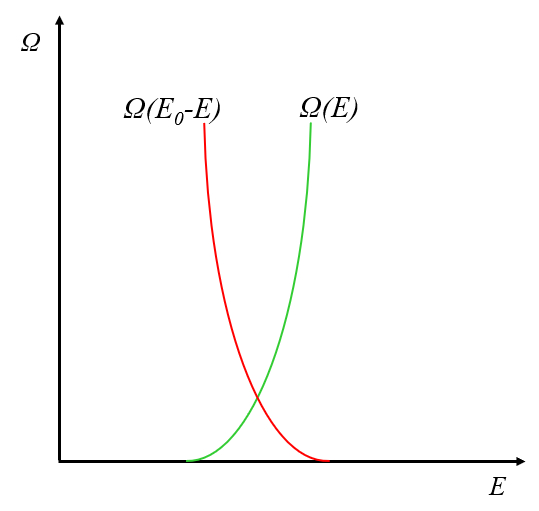
Isso ocorre porque, à medida que a energia aumenta, a energia do reservatório diminui, o que por sua vez reduz o número de estados aos quais ele pode acessar.
ID:(11542, 0)
Formação de um máximo
Nota 
Quando multiplicamos o número de casos, obtemos uma função com um pico muito pronunciado.

O sistema tem uma probabilidade maior de ser encontrado na energia onde ocorre o pico da curva de probabilidade.
ID:(11543, 0)
Condição e temperatura de equilíbrio
Storyboard 
Para modelar sistemas usando a mecânica estatística, é necessário investigar como os parâmetros que descrevem o sistema macroscópico podem influenciar os conjuntos estatísticos. No caso de partículas, a temperatura é estabelecida como um parâmetro que reflete se os sistemas estão em equilíbrio, mantendo suas energias em um nível constante.
Variáveis
Cálculos
Cálculos
Equações
Exemplos
Podemos estudar o que acontece quando colocamos dois sistemas de part culas em contato, de modo que possam trocar energia, mas n o part culas.
Vamos tamb m supor que o sistema est isolado do ambiente, o que significa que possui uma energia total de $E_0$.
Suponhamos que inicialmente o primeiro sistema tenha uma energia de $E$, o que est associado a $\Omega(E)$ estados.
Uma vez que a energia total $E_0$, o segundo sistema s pode ter energia $E_0-E$ e um n mero de estados associados $\Omega(E_0-E)$.
Quando os colocamos em contato, eles podem trocar energia at atingir algum equil brio. Nesse sentido, o valor de $E$ vai variar, e a probabilidade de encontrar os sistemas de modo que o primeiro tenha um valor de $E$ tamb m vai variar.
Cada sistema $\Omega$ possui um n mero de estados poss veis que depende de sua energia $E$. Portanto, se o sistema que estamos estudando tem uma energia $E$, o n mero de estados poss veis ser $\Omega(E)$.
O sistema em estudo est em contato com um reservat rio que fornece energia $E$, de modo que a energia total $E_0$ menos a do sistema imerso, $E$. Portanto, o reservat rio possui $\Omega(E_0 - E)$ estados poss veis. A probabilidade de encontrar o sistema total com uma energia $E$ no sistema imerso expressa como o produto do n mero de estados com
onde $C$ uma constante de normaliza o. A energia $E$ ser aquela para a qual a probabilidade m xima.
Quando comparamos como o n mero de estados varia com a energia $E$, observamos que o comportamento do sistema e do reservat rio oposto:
Isso ocorre porque, medida que a energia aumenta, a energia do reservat rio diminui, o que por sua vez reduz o n mero de estados aos quais ele pode acessar.
Quando multiplicamos o n mero de casos, obtemos uma fun o com um pico muito pronunciado.
O sistema tem uma probabilidade maior de ser encontrado na energia onde ocorre o pico da curva de probabilidade.
Se a probabilidade de dois sistemas isolados, cada um com uma energia total de $E_0$ e sendo a energia de um dos sistemas $E$, dada por
Podemos estimar a energia prov vel $E$ na qual eles ser o encontrados procurando o m ximo da probabilidade. Para fazer isso, precisamos derivar em rela o energia $E$ e igualar a derivada a zero.
$\displaystyle\frac{\partial P}{\partial E}=\displaystyle\frac{\partial\Omega}{\partial E}\Omega'+\Omega\displaystyle\frac{\partial\Omega'}{\partial E}=0$
Se dividirmos a express o por $\Omega\Omega'$ e substituirmos a diferen a de energia $E_0-E$ por $E'$, podemos reformular a condi o para determinar a situa o mais prov vel da seguinte forma:
Se existe uma probabilidade $P(E)$ de encontrar
$\displaystyle\frac{1}{\Omega}\displaystyle\frac{\partial\Omega}{\partial E}-\displaystyle\frac{1}{\Omega'}\displaystyle\frac{\partial\Omega'}{\partial E'}=0$
O sinal negativo resulta da mudan a de vari veis, j que com
$E'=E_0-E$
a derivada em rela o a $E'$ resulta em
Quando um sistema est em contato com um reservat rio de energia $E_0$, prov vel encontr -lo com uma energia $E$ para a qual a probabilidade com
atinge o seu m ximo. A energia pode ser determinada derivando esta express o em rela o energia $E$ e igualando-a a zero. Isso equivalente a derivar o logaritmo da probabilidade:
$\ln P(E) = \ln C + \ln\Omega(E) + \ln\Omega(E_0-E)$
Levando a:
$\displaystyle\frac{\partial\ln\Omega}{\partial E} + \displaystyle\frac{\partial\ln\Omega}{\partial E} = 0$
Se fizermos uma mudan a de vari vel:
$E' = E_0 - E$
Obtemos a condi o de equil brio com
A condi o de equil brio de um sistema em contato com um reservat rio expressa com
Isso nos permite introduzir uma fun o $\beta$ com
Esta fun o caracteriza o estado do sistema e se torna relevante quando o sistema est em equil brio com outro sistema.
Quando um sistema est em contato com um reservat rio de energia $E_0$, prov vel encontr -lo com uma energia $E$ para a qual, com
atinge o seu m ximo. A energia pode ser determinada derivando esta express o em rela o energia $E$ e igualando-a a zero. Isso equivalente a derivar o logaritmo da probabilidade:
$\ln P(E) = \ln C + \ln\Omega(E) + \ln\Omega(E_0-E)$
Assim, com
Se realizarmos uma mudan a de vari vel
$E' = E_0 - E$
obtemos a condi o de equil brio com
Se assumirmos que encontramos o sistema na energia para a qual a probabilidade m xima, podemos associar esse fato situa o de equil brio de um sistema, onde a probabilidade m xima.
Por outro lado, sabemos que dois sistemas est o em equil brio t rmico quando suas temperaturas s o iguais. Portanto, o fato de que as fun es $\beta$ sejam iguais nos sugere que $\beta$ est relacionado temperatura.
Uma vez que as unidades de $\beta$ s o o rec proco da energia, podemos defini-lo da seguinte forma com
Ao introduzir a rela o com
a condi o de equil brio com
simplificada para apenas
ID:(436, 0)
