Druyd:Knowledge

Beispiel für den Zufallspfad (Rando Walk)

Storyboard

Der zufällige Pfad ist ein typisches Beispiel, da ausgehend von mikroskopischen Wahrscheinlichkeiten (Schritt nach rechts oder links) eine Wahrscheinlichkeitsverteilung entwickelt werden kann, die die wahrscheinlichsten Stellen berücksichtigt, an denen sich der Wanderer befindet.

>Modell

ID:(308, 0)

Random Walk Problem

Definition

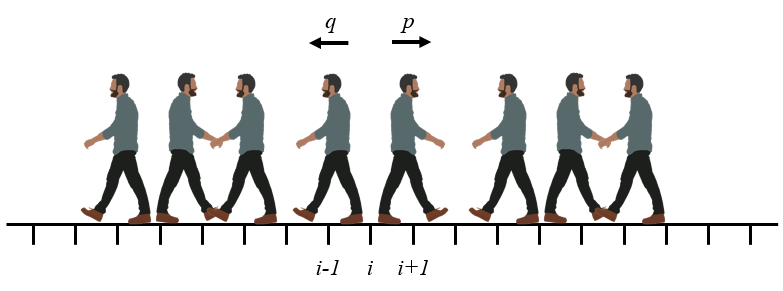
Das Problem des zufälligen Pfades ist ein Beispiel dafür, wie man aus der mikroskopischen Beschreibung die wahrscheinliche zeitliche Entwicklung vorhersagen kann. In diesem Fall wird angenommen, dass ein Akteur (Partikel, Person usw.) zufällig auswählt, ob er einen Schritt nach rechts oder nach links macht. Es wird angenommen, dass die Schritte eine Länge a haben und dass die Wahrscheinlichkeit, nach rechts zu gehen, p und nach links q ist:

ID:(11396, 0)

Binomialverteilung

Bild

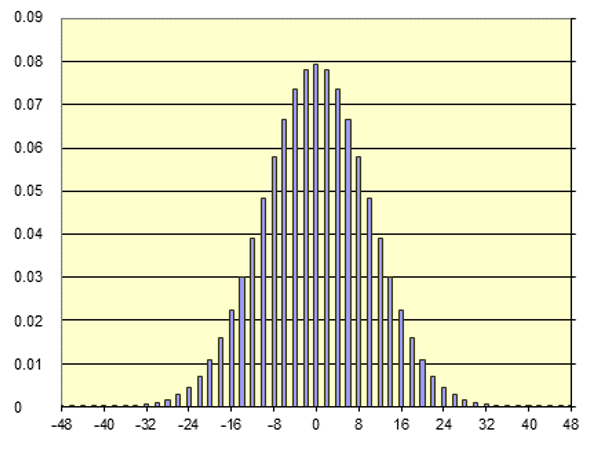
Das Ergebnis der Berechnung entspricht einer sogenannten Binomialverteilung. Jede Zeile gibt an, wie oft der Akteur nach einer Anzahl von N von Schritten an dieser Position landet. Dies entspricht der Wahrscheinlichkeit, es nach N Schritten an dieser Stelle zu finden:

ID:(11397, 0)

Beispiel für den Zufallspfad (Rando Walk)

Beschreibung

Variablen

Symbol

Text

Variable

Wert

Einheiten

Berechnen

MKS-Wert

MKS-Einheiten

$C_{n_1n_2}$

C_n1n2

Combinaciones posibles de (n_1,n_2) caminos

$n_2$

n_2

Número de pasos hacia la derecha

$q$

Número de pasos hacia la derecha

$n_1$

n_1

Número de pasos hacia la izquierda

$N$

Número total de pasos

$n$

Número totales de pasos a la izquierda

$s$

Posición camino aleatorio

$P_N(m)$

P_Nm

Probabilidad de

$n_1$ de

$N$ pasos hacia la izquierda

$p_{n_1n_2}$

p_n1n2

Probabilidad de avanzar una combinación (n_1,n_2)

$p$

Probabilidad de pasos hacia la izquierda

$p_{n_1,n_2}$

p_n1n2

Probabilidad de realizar (n_1,n_2) pasos

$W_N(n_1,n_2)$

W_n1n2

Probabilidad de realizar (n_1,n_2) pasos cualquier secuencia

$a$

Schrittlänge

$\Delta t$

Tiempo del paso

$t$

Tiempo final

Berechnungen

Gleichung

Zahl

Zuerst die Gleichung auswählen:

, dann die Variable auswählen:

Symbol

Gleichung

Gelöst

Übersetzt

Berechnungen

Symbol

Gleichung

Gelöst

Übersetzt

Variable

Gegeben

Berechnen

Ziel :

Gleichung

Zu verwenden

Gleichungen

$t = N \Delta t$

t = N * Dt

(ID 501)

$x=(n_1-n_2)a$

x=(n_2-n_1)a

(ID 503)

$p_{n_1n_2}=p^{n_1}q^{n_2}$

p_{n_1n_2}=p^{n_1}q^{n_2}

(ID 504)

$C_{n_1n_2}=\displaystyle\frac{N!}{n_1!n_2!}$

C_n1n2=N!/(n_1!n_2!)

(ID 505)

$N=n_1+n_2$

N = n_1 + n_2

(ID 3358)

$W_N(n) =\displaystyle\frac{ N !}{ n !( N - n )!} p ^ n (1- p )^{ N - n }$

W_N(n) =math.factorial( N )* p ^ n *(1- p )^( N - n )/(math.factorial( n )*math.factorial( N - n ))

(ID 8961)

$p+q=1$

p+q=1

(ID 8965)

$W_N(n_1,n_2)=\displaystyle\frac{N!}{n_1!n_2!}p^{n_1}q^{n_2}$

W_N(n_1,n_2)=\displaystyle\frac{N!}{n_1!n_2!}p^{n_1}q^{n_2}

(ID 8970)

$W_N(n_1,n_2)=C_{n_1n_2}p_{n_1n_2}$

W_N(n_1,n_2)=C_{n_1n_2}p_{n_1n_2}

(ID 8980)

Beispiele

Random Walk Problem

Das Problem des zuf lligen Pfades ist ein Beispiel daf r, wie man aus der mikroskopischen Beschreibung die wahrscheinliche zeitliche Entwicklung vorhersagen kann. In diesem Fall wird angenommen, dass ein Akteur (Partikel, Person usw.) zuf llig ausw hlt, ob er einen Schritt nach rechts oder nach links macht. Es wird angenommen, dass die Schritte eine L nge a haben und dass die Wahrscheinlichkeit, nach rechts zu gehen, p und nach links q ist:

(ID 11396)

Verstrichene Zeit

El tiempo transcurrido es igual al numero de paso por el tiempo que demora un paso, con es:

$t = N \Delta t$

(ID 501)

Modellierung der Szene der Random Walk

En el modelar el camino aleatorio se deben considerar que se hace un cierto numero de pasos hacia la derecha y otro tanto hacia la izquierda ocurriendo esto en un tiempo que depende del numero de pasos y del tiempo que demora cada uno.

Dicho tiempo es por tanto, con número total de pasos $-$ , tiempo del paso $s$ und tiempo final $s$ igual a

$t = N \Delta t$

El camino recorrido correspondiente es entonces, con número total de pasos $-$ , tiempo del paso $s$ und tiempo final $s$ igual a

$x=(n_1-n_2)a$

Nota: esta discretizaci n no es una condici n para modelar el caso ya que se pueden introducir distribuciones de probabilidades de que el paso ocurra en un tiempo t como el largo del paso se puede asociar a una distribuci n de largos de pasos.

(ID 503)

Chance auf eine Verschiebung

El desplazamiento ocurrir con ciertas probabilidades en direcci n de la derecha e izquierda. Si esta fuera igual tender an a ocurrir la misma cantidad de pasos hacia la derecha como la izquierda con lo que la posici n final terminar a siendo pr xima al origen. Si una de ambas probabilidades es mucho mayor tendera a favorecerse uno de ambos pasos y se tender a a terminar desplazado en la direcci n mas favorable.

Si los pasos son independientes el uno del otro la probabilidad de una cierta secuencia solo depender la la multiplicaci n de las probabilidades de los pasos individuales.Por ello con se tiene que la probabilidad de una secuencia especifica de pasos es:

$p_{n_1n_2}=p^{n_1}q^{n_2}$

(ID 504)

Gesamt Schritte

El numero total de pasos es igual a la suma de los pasos hacia la derecha y aquellos hacia la izquierda, por lo que con

(ID 3358)

M gliche Ans tze

Hasta aqu se consideraron secuencias especificas de pasos dados hacia la derecha y la izquierda sin embargo existen una serie de alternativas con que se puede realizar la caminata todas terminando en el mismo punto.

Por ello se debe calcula el numero de combinaciones posibles lo que con esta dado por

$C_{n_1n_2}=\displaystyle\frac{N!}{n_1!n_2!}$

(ID 505)

Probabilidad de dar un numero de pasos a la derecha y a la izquierda (1)

Con la probabilidad de una secuencia en particular y el numero de secuencias posibles se puede calcular con el producto la probabilidad de cualquier secuencia que termina considera el mismo numero de pasos hacia la derecha como hacia la izquierda.

Por ello con se tiene que

$W_N(n_1,n_2)=C_{n_1n_2}p_{n_1n_2}$

(ID 8980)

Probabilidad de dar un numero de pasos a la derecha y a la izquierda (2)

Como la probabilidad de realizar un numero de pasos hacia la derecha y otro hacia la izquierda en cualquier secuencia posible es con combinaciones posibles de (n_1,n_2) caminos $-$ , probabilidad de realizar (n_1,n_2) pasos $-$ und probabilidad de realizar (n_1,n_2) pasos cualquier secuencia $-$ igual a

$W_N(n_1,n_2)=C_{n_1n_2}p_{n_1n_2}$

se tiene que con combinaciones posibles de (n_1,n_2) caminos $-$ , número de pasos hacia la derecha $-$ , número de pasos hacia la izquierda $-$ und número total de pasos $-$ el numero de combinaciones es

$C_{n_1n_2}=\displaystyle\frac{N!}{n_1!n_2!}$

y con número de pasos hacia la derecha $-$ , número de pasos hacia la derecha $-$ , número de pasos hacia la izquierda $-$ , probabilidad de avanzar una combinación (n_1,n_2) $-$ und probabilidad de pasos hacia la izquierda $-$ la probabilidad de dar en una secuencia espec fica

$p_{n_1n_2}=p^{n_1}q^{n_2}$

que con número de pasos hacia la derecha $-$ , número de pasos hacia la derecha $-$ , número de pasos hacia la izquierda $-$ , probabilidad de avanzar una combinación (n_1,n_2) $-$ und probabilidad de pasos hacia la izquierda $-$ la probabilidad es

$W_N(n_1,n_2)=\displaystyle\frac{N!}{n_1!n_2!}p^{n_1}q^{n_2}$

(ID 8970)

Summe der Wahrscheinlichkeiten

Si el desplazamiento solo es hacia la derecha o la izquierda y no existe otra alternativa de no realizar el paso, la suma de las probabilidades de dar pasos a hacia la derecha e izquierda debe ser igual a la unidad.

Por ello con se tiene que

$p+q=1$

(ID 8965)

Distribuci n binomial

Con número de pasos hacia la derecha $-$ , número de pasos hacia la derecha $-$ , número de pasos hacia la izquierda $-$ , número total de pasos $-$ , probabilidad de pasos hacia la izquierda $-$ und probabilidad de realizar (n_1,n_2) pasos $-$ la probabilidad de que se de un numero definido de pasos a la derecha e izquierda esta dada por

$W_N(n_1,n_2)=\displaystyle\frac{N!}{n_1!n_2!}p^{n_1}q^{n_2}$

con número de pasos hacia la derecha $-$ , número de pasos hacia la izquierda $-$ und número total de pasos $-$ el n mero total de pasos es

$N=n_1+n_2$

y solo existe la probabilidad de ir a la derecha o a la izquierda, con número de pasos hacia la derecha $-$ und probabilidad de pasos hacia la izquierda $-$ se tiene para las probabilidades que

$p+q=1$

por lo que con número de pasos hacia la derecha $-$ und probabilidad de pasos hacia la izquierda $-$ se tiene la distribuci n binomial

$W_N(n) =\displaystyle\frac{ N !}{ n !( N - n )!} p ^ n (1- p )^{ N - n }$

(ID 8961)

Binomialverteilung

(ID 11397)

ID:(308, 0)