Druyd:Knowledge

Example of the Random Path (Rando Walk)

Storyboard

The random path is a typical example as starting from microscopic probabilities (the step to the right or left) it is possible to develop a probability distribution that accounts for the most probable places in which the walker can be found.

>Model

ID:(308, 0)

Random walk problem

Definition

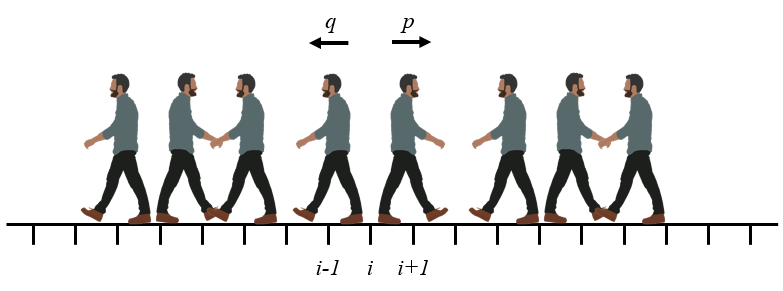
The problem of the random path is an example of how one can from the microscopic description predict the probable temporal evolution. In this case it is assumed that an actor (particle, person, etc.) randomly chooses whether to take a step to the right or to the left. It is assumed that the steps have a length a and that the probability of going to the right is p and to the left q:

ID:(11396, 0)

Binomial distribution

Image

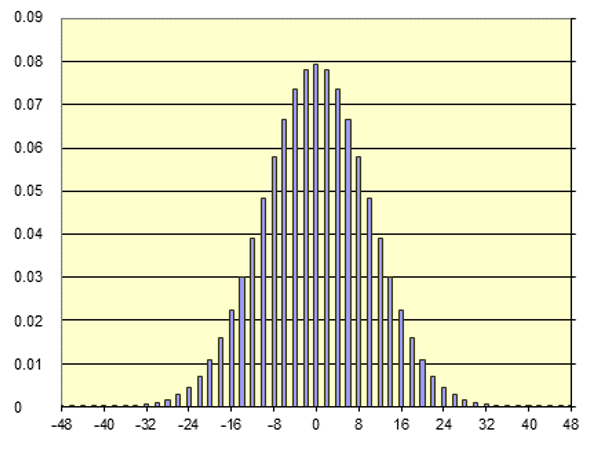
The result of the calculation corresponds to what is called a binomial distribution. Each line indicates the fraction of times that after a number N of steps the actor ends up in that position. This corresponds to the probability of finding it after N steps at that location:

ID:(11397, 0)

Example of the Random Path (Rando Walk)

Description

Variables

Symbol

Text

Variable

Value

Units

Calculate

MKS Value

MKS Units

$C_{n_1n_2}$

C_n1n2

Combinaciones posibles de (n_1,n_2) caminos

$n_2$

n_2

Número de pasos hacia la derecha

$q$

Número de pasos hacia la derecha

$n_1$

n_1

Número de pasos hacia la izquierda

$N$

Número total de pasos

$n$

Número totales de pasos a la izquierda

$s$

Posición camino aleatorio

$P_N(m)$

P_Nm

Probabilidad de

$n_1$ de

$N$ pasos hacia la izquierda

$p_{n_1n_2}$

p_n1n2

Probabilidad de avanzar una combinación (n_1,n_2)

$p$

Probabilidad de pasos hacia la izquierda

$p_{n_1,n_2}$

p_n1n2

Probabilidad de realizar (n_1,n_2) pasos

$W_N(n_1,n_2)$

W_n1n2

Probabilidad de realizar (n_1,n_2) pasos cualquier secuencia

$a$

Step size

$\Delta t$

Tiempo del paso

$t$

Tiempo final

Calculations

Equation

Number

First, select the equation:

, then, select the variable:

Symbol

Equation

Solved

Translated

Calculations

Symbol

Equation

Solved

Translated

Variable

Given

Calculate

Target :

Equation

To be used

Equations

$t = N \Delta t$

t = N * Dt

(ID 501)

$x=(n_1-n_2)a$

x=(n_2-n_1)a

(ID 503)

$p_{n_1n_2}=p^{n_1}q^{n_2}$

p_{n_1n_2}=p^{n_1}q^{n_2}

(ID 504)

$C_{n_1n_2}=\displaystyle\frac{N!}{n_1!n_2!}$

C_n1n2=N!/(n_1!n_2!)

(ID 505)

$N=n_1+n_2$

N = n_1 + n_2

(ID 3358)

$W_N(n) =\displaystyle\frac{ N !}{ n !( N - n )!} p ^ n (1- p )^{ N - n }$

W_N(n) =math.factorial( N )* p ^ n *(1- p )^( N - n )/(math.factorial( n )*math.factorial( N - n ))

(ID 8961)

$p+q=1$

p+q=1

(ID 8965)

$W_N(n_1,n_2)=\displaystyle\frac{N!}{n_1!n_2!}p^{n_1}q^{n_2}$

W_N(n_1,n_2)=\displaystyle\frac{N!}{n_1!n_2!}p^{n_1}q^{n_2}

(ID 8970)

$W_N(n_1,n_2)=C_{n_1n_2}p_{n_1n_2}$

W_N(n_1,n_2)=C_{n_1n_2}p_{n_1n_2}

(ID 8980)

Examples

Random walk problem

(ID 11396)

The time passed

El tiempo transcurrido es igual al numero de paso por el tiempo que demora un paso, con es:

$t = N \Delta t$

(ID 501)

Modeling the scene of Random Walk

En el modelar el camino aleatorio se deben considerar que se hace un cierto numero de pasos hacia la derecha y otro tanto hacia la izquierda ocurriendo esto en un tiempo que depende del numero de pasos y del tiempo que demora cada uno.

Dicho tiempo es por tanto, con número total de pasos $-$ , tiempo del paso $s$ and tiempo final $s$ igual a

$t = N \Delta t$

El camino recorrido correspondiente es entonces, con número total de pasos $-$ , tiempo del paso $s$ and tiempo final $s$ igual a

$x=(n_1-n_2)a$

Nota: esta discretizaci n no es una condici n para modelar el caso ya que se pueden introducir distribuciones de probabilidades de que el paso ocurra en un tiempo t como el largo del paso se puede asociar a una distribuci n de largos de pasos.

(ID 503)

Chance of a displacement

El desplazamiento ocurrir con ciertas probabilidades en direcci n de la derecha e izquierda. Si esta fuera igual tender an a ocurrir la misma cantidad de pasos hacia la derecha como la izquierda con lo que la posici n final terminar a siendo pr xima al origen. Si una de ambas probabilidades es mucho mayor tendera a favorecerse uno de ambos pasos y se tender a a terminar desplazado en la direcci n mas favorable.

Si los pasos son independientes el uno del otro la probabilidad de una cierta secuencia solo depender la la multiplicaci n de las probabilidades de los pasos individuales.Por ello con se tiene que la probabilidad de una secuencia especifica de pasos es:

$p_{n_1n_2}=p^{n_1}q^{n_2}$

(ID 504)

Total steps

El numero total de pasos es igual a la suma de los pasos hacia la derecha y aquellos hacia la izquierda, por lo que con

(ID 3358)

Possible ways

Hasta aqu se consideraron secuencias especificas de pasos dados hacia la derecha y la izquierda sin embargo existen una serie de alternativas con que se puede realizar la caminata todas terminando en el mismo punto.

Por ello se debe calcula el numero de combinaciones posibles lo que con esta dado por

$C_{n_1n_2}=\displaystyle\frac{N!}{n_1!n_2!}$

(ID 505)

Probabilidad de dar un numero de pasos a la derecha y a la izquierda (1)

Con la probabilidad de una secuencia en particular y el numero de secuencias posibles se puede calcular con el producto la probabilidad de cualquier secuencia que termina considera el mismo numero de pasos hacia la derecha como hacia la izquierda.

Por ello con se tiene que

$W_N(n_1,n_2)=C_{n_1n_2}p_{n_1n_2}$

(ID 8980)

Probabilidad de dar un numero de pasos a la derecha y a la izquierda (2)

Como la probabilidad de realizar un numero de pasos hacia la derecha y otro hacia la izquierda en cualquier secuencia posible es con combinaciones posibles de (n_1,n_2) caminos $-$ , probabilidad de realizar (n_1,n_2) pasos $-$ and probabilidad de realizar (n_1,n_2) pasos cualquier secuencia $-$ igual a

$W_N(n_1,n_2)=C_{n_1n_2}p_{n_1n_2}$

se tiene que con combinaciones posibles de (n_1,n_2) caminos $-$ , número de pasos hacia la derecha $-$ , número de pasos hacia la izquierda $-$ and número total de pasos $-$ el numero de combinaciones es

$C_{n_1n_2}=\displaystyle\frac{N!}{n_1!n_2!}$

y con número de pasos hacia la derecha $-$ , número de pasos hacia la derecha $-$ , número de pasos hacia la izquierda $-$ , probabilidad de avanzar una combinación (n_1,n_2) $-$ and probabilidad de pasos hacia la izquierda $-$ la probabilidad de dar en una secuencia espec fica

$p_{n_1n_2}=p^{n_1}q^{n_2}$

que con número de pasos hacia la derecha $-$ , número de pasos hacia la derecha $-$ , número de pasos hacia la izquierda $-$ , probabilidad de avanzar una combinación (n_1,n_2) $-$ and probabilidad de pasos hacia la izquierda $-$ la probabilidad es

$W_N(n_1,n_2)=\displaystyle\frac{N!}{n_1!n_2!}p^{n_1}q^{n_2}$

(ID 8970)

Sum of probabilities

Si el desplazamiento solo es hacia la derecha o la izquierda y no existe otra alternativa de no realizar el paso, la suma de las probabilidades de dar pasos a hacia la derecha e izquierda debe ser igual a la unidad.

Por ello con se tiene que

$p+q=1$

(ID 8965)

Distribuci n binomial

Con número de pasos hacia la derecha $-$ , número de pasos hacia la derecha $-$ , número de pasos hacia la izquierda $-$ , número total de pasos $-$ , probabilidad de pasos hacia la izquierda $-$ and probabilidad de realizar (n_1,n_2) pasos $-$ la probabilidad de que se de un numero definido de pasos a la derecha e izquierda esta dada por

$W_N(n_1,n_2)=\displaystyle\frac{N!}{n_1!n_2!}p^{n_1}q^{n_2}$

con número de pasos hacia la derecha $-$ , número de pasos hacia la izquierda $-$ and número total de pasos $-$ el n mero total de pasos es

$N=n_1+n_2$

y solo existe la probabilidad de ir a la derecha o a la izquierda, con número de pasos hacia la derecha $-$ and probabilidad de pasos hacia la izquierda $-$ se tiene para las probabilidades que

$p+q=1$

por lo que con número de pasos hacia la derecha $-$ and probabilidad de pasos hacia la izquierda $-$ se tiene la distribuci n binomial

$W_N(n) =\displaystyle\frac{ N !}{ n !( N - n )!} p ^ n (1- p )^{ N - n }$

(ID 8961)

Binomial distribution

(ID 11397)

ID:(308, 0)