Druyd:Knowledge

Wahrscheinlichkeitsgrundlagen

Storyboard

Wenn das Ergebnis eines Prozesses nicht deterministisch ist, können wir mit Wahrscheinlichkeiten arbeiten, um die Ergebnisse zu untersuchen und zumindest eine statistische Prognose des Ergebnisses des Ereignisses zu erstellen.

>Modell

ID:(429, 0)

Das Problem

Definition

Si arrojamos un dado no tenemos forma de poder predecir el número que caerá. Solo sabemos que puede ser un 1, un 2, un 3, un 4, un 5 o un 6.

Por ello debemos considerar situaciones en física en que no exista un resultado único y en que estos ocurren con una cierta frecuencia. Esta frecuencia se asocia a lo que denominamos probabilidad.

En un sistema físico el resultado de un experimento puede ser continuo por lo que el pronostico ni si quiera se puede reducir a indicar pocas alternativas si no que rangos de valores posibles. En este caso no existe una frecuencia de un resultado en particular si no de una gama de valores continua.

En el caso de que el resultado pueda ser cualquier valor dentro de un rango continuo se puede aproximar la discreción mediante la definición de rangos discretos para los que se puede determinar una frecuencia e introducir el concepto de probabilidad.

ID:(455, 0)

Konzept der Wahrscheinlichkeit

Bild

Si se expresa la probabilidad en forma de porcentajes entonces una probabilidad indica la fracción de las veces para cada 100 eventos que ocurran.

Ejemplo, si la probabilidad es 20% eso significa que ocurrirá en 20 veces cada 100 veces que el evento ocurra.

Aun que se puede expresar la probabilidad como porcentajes se acostumbra a indicarla como una fracción. O sea en el caso de 20% se indica que la probabilidad es de 0.2.

ID:(460, 0)

Mathematische Notation

Notiz

ID:(164, 0)

Ein Set

Zitat

ID:(1830, 0)

Set und Complement

Übung

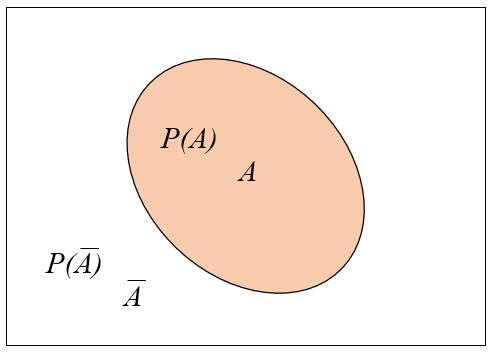
En teoría de conjunto se puede representar los eventos A como un conjunto y el resto del espacio como el complemento \bar{A} que son los eventos que no corresponden a A.

Las correspondientes probabilidades son aquellas proporciones que corresponden a a que ocurra o no el evento A.

ID:(1831, 0)

Beispiel Diskrete Fall

Gleichung

Si se arroja un dado N=100 veces y se contabilizan las veces n_i que salen las distintas caras i=1,2,3,4,5,6 se pueden calcular las probabilidades p_i.

Si el número de desenlaces son n_1=15, n_2=18, n_3=19, n_4=22, n_5=12 y n_6=14 las probabilidades serán:

$i$	$n_i$	$p_i$
1	15	0.15
2	18	0.18
3	19	0.19
4	22	0.22
5	12	0.12
6	14	0.14

ID:(458, 0)

Lösung für diskrete Gehäuse

Script

ID:(456, 0)

Definition von Messwerten

Variable

ID:(163, 0)

Beispiel Continuous Fall

Audio

En el caso de una variable continua se debe primero segmentar esta en sub-rangos que pueden o no ser de igual largo.

Si estamos estudiando la temperatura media de una sala y esta fluctúa en el día entre 18^{\circ} C y no más que 24^{\circ} C, se puede fraccionar en intervalos de un grado. Con ello los seis rangos serán 18-19^{\circ} C, 19-20^{\circ} C, 20-21^{\circ} C, 21-22^{\circ} C, 22-23^{\circ} C y 23-24^{\circ} C. Si realizamos a lo largo del día 100 mediciones se puede calcular la probabilidad de que esta se encuentre en cualquiera de los rangos.

Si el número de veces que se miden las temperaturas en cada rango y estos son (donde el indice i es la temperatura mínimo de los rangos) son n_{18} = 5, n_{19} = 25, n_{20} = 33, n_{21} = 21, n_{22} = 14 y n_{23} = 2 las probabilidades serán:

$i$	$n_i$	$p_i$
18-19	30	0.30
20-21	54	0.54
22-23	16	0.16

ID:(459, 0)

Lösung für die kontinuierliche Fall

Video

ID:(457, 0)

Wahrscheinlichkeitsgrundlagen

Beschreibung

Variablen

Symbol

Text

Variable

Wert

Einheiten

Berechnen

MKS-Wert

MKS-Einheiten

$n_i$

n_i

Anzahl der Ereignisse vom Typ

$i$

$N$

Gesamtzahl der Werte

$P(\bar{A})$

PcA

Komplement der Menge der Ereignisse

$A$

$P(A)$

Wahrscheinlichkeit eines Ereignisses vom Typ

$A$

$p_i$

p_i

Wahrscheinlichkeit eines Ereignisses vom Typ

$i$

Berechnungen

Gleichung

Zahl

Zuerst die Gleichung auswählen:

, dann die Variable auswählen:

Symbol

Gleichung

Gelöst

Übersetzt

Berechnungen

Symbol

Gleichung

Gelöst

Übersetzt

Variable

Gegeben

Berechnen

Ziel :

Gleichung

Zu verwenden

Gleichungen

$P(A)+P(\bar{A})=1$

P(A)+P(-A)=1

(ID 3188)

$p_i=\displaystyle\frac{n_i}{N}$

p_i=n_i/N

(ID 3284)

Beispiele

Das Problem

Si arrojamos un dado no tenemos forma de poder predecir el n mero que caer . Solo sabemos que puede ser un 1, un 2, un 3, un 4, un 5 o un 6.

Por ello debemos considerar situaciones en f sica en que no exista un resultado nico y en que estos ocurren con una cierta frecuencia. Esta frecuencia se asocia a lo que denominamos probabilidad.

En un sistema f sico el resultado de un experimento puede ser continuo por lo que el pronostico ni si quiera se puede reducir a indicar pocas alternativas si no que rangos de valores posibles. En este caso no existe una frecuencia de un resultado en particular si no de una gama de valores continua.

En el caso de que el resultado pueda ser cualquier valor dentro de un rango continuo se puede aproximar la discreci n mediante la definici n de rangos discretos para los que se puede determinar una frecuencia e introducir el concepto de probabilidad.

(ID 455)

Konzept der Wahrscheinlichkeit

Si se expresa la probabilidad en forma de porcentajes entonces una probabilidad indica la fracci n de las veces para cada 100 eventos que ocurran.

Ejemplo, si la probabilidad es 20% eso significa que ocurrir en 20 veces cada 100 veces que el evento ocurra.

Aun que se puede expresar la probabilidad como porcentajes se acostumbra a indicarla como una fracci n. O sea en el caso de 20% se indica que la probabilidad es de 0.2.

(ID 460)

Wahrscheinlichkeit

Como la probabilidad se define como la fracci n de que ocurra un evento en particular se puede estimar esta simplemente determinando el numero de veces que se da el evento considerado en proporci n a todos los eventos de distintos tipos que se den.

Por ello con se tiene que

$p_i=\displaystyle\frac{n_i}{N}$

\\n\\nComo ejemplo si se tira 20 veces un dado y en 3 ocasiones se obtiene un 6 se puede estimar que la probabilidad de que surja un 6 es del orden de\\n\\n

$p_6=\displaystyle\frac{3}{20}=0.15$

(ID 3284)

Mathematische Notation

(ID 164)

Ein Set

(ID 1830)

Die Erg nzung

$P(A)+P(\bar{A})=1$

(ID 3188)

Set und Complement

En teor a de conjunto se puede representar los eventos A como un conjunto y el resto del espacio como el complemento \bar{A} que son los eventos que no corresponden a A.

Las correspondientes probabilidades son aquellas proporciones que corresponden a a que ocurra o no el evento A.

(ID 1831)

Beispiel Diskrete Fall

Si se arroja un dado N=100 veces y se contabilizan las veces n_i que salen las distintas caras i=1,2,3,4,5,6 se pueden calcular las probabilidades p_i.

Si el n mero de desenlaces son n_1=15, n_2=18, n_3=19, n_4=22, n_5=12 y n_6=14 las probabilidades ser n:

$i$	$n_i$	$p_i$
1	15	0.15
2	18	0.18
3	19	0.19
4	22	0.22
5	12	0.12
6	14	0.14

(ID 458)

L sung f r diskrete Geh use

(ID 456)

Definition von Messwerten

(ID 163)

Beispiel Continuous Fall

En el caso de una variable continua se debe primero segmentar esta en sub-rangos que pueden o no ser de igual largo.

Si estamos estudiando la temperatura media de una sala y esta fluct a en el d a entre 18^{\circ} C y no m s que 24^{\circ} C, se puede fraccionar en intervalos de un grado. Con ello los seis rangos ser n 18-19^{\circ} C, 19-20^{\circ} C, 20-21^{\circ} C, 21-22^{\circ} C, 22-23^{\circ} C y 23-24^{\circ} C. Si realizamos a lo largo del d a 100 mediciones se puede calcular la probabilidad de que esta se encuentre en cualquiera de los rangos.

Si el n mero de veces que se miden las temperaturas en cada rango y estos son (donde el indice i es la temperatura m nimo de los rangos) son n_{18} = 5, n_{19} = 25, n_{20} = 33, n_{21} = 21, n_{22} = 14 y n_{23} = 2 las probabilidades ser n:

$i$	$n_i$	$p_i$
18-19	30	0.30
20-21	54	0.54
22-23	16	0.16

(ID 459)

L sung f r die kontinuierliche Fall

(ID 457)

ID:(429, 0)