Velocidad angular constante
Storyboard 
Para describir la evolución del ángulo en el tiempo, es fundamental analizar su variación a lo largo del mismo.
La relación entre la variación del ángulo y el arco recorrido en el tiempo transcurrido es lo que define la velocidad angular. Esta se obtiene al dividir la variación angular por el tiempo transcurrido, dando lugar a la denominada velocidad angular.
Cuando se considera un intervalo de tiempo finito, la velocidad angular representa la velocidad angular promedio durante ese período.
ID:(611, 0)
Angulo recorrido
Imagen 
Una vez introducido el concepto de tiempo transcurrido, podemos definir el movimiento en términos del ángulo recorrido. Para ello, es necesario medir:
• el ángulo actual, que se determina como la diferencia de ángulo con respecto a un origen desde el cual se está midiendo;
• el ángulo inicial, que se determina como la diferencia de ángulo al mismo origen previo, y se calcula como la diferencia entre el primero y el segundo.
ID:(12516, 0)
Velocidad angular en forma gráfica
Ejercicio 
La velocidad angular media se define como el ángulo recorrido en el tiempo transcurrido. Como la rotación requiere de un eje, éste se dibuja de forma ortogonal al disco que representa el cuerpo que rota. Para integrar el eje, la velocidad angular se define como un vector en el que la magnitud es el ángulo recorrido por unidad de tiempo y la dirección se define en función de la dirección del eje:
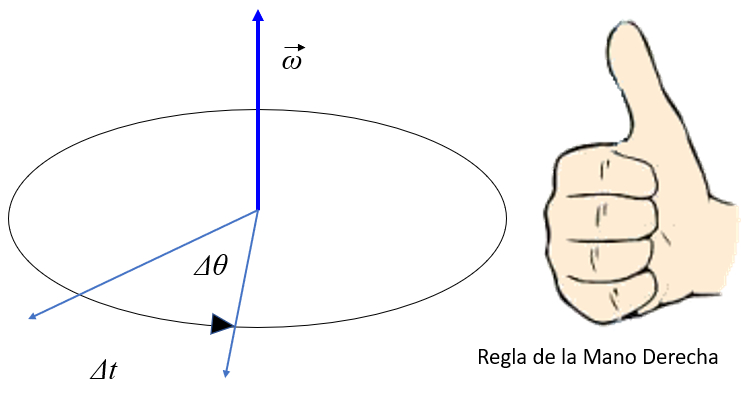
ID:(10967, 0)
Velocidad tangencial
Script 
Si un objeto se somete a un modo de mantener un radio constante, girará como se indica en la figura. Al observar la figura, se notará que la masa realiza un movimiento de traslación con una velocidad tangencial que es igual al radio por la velocidad angular:
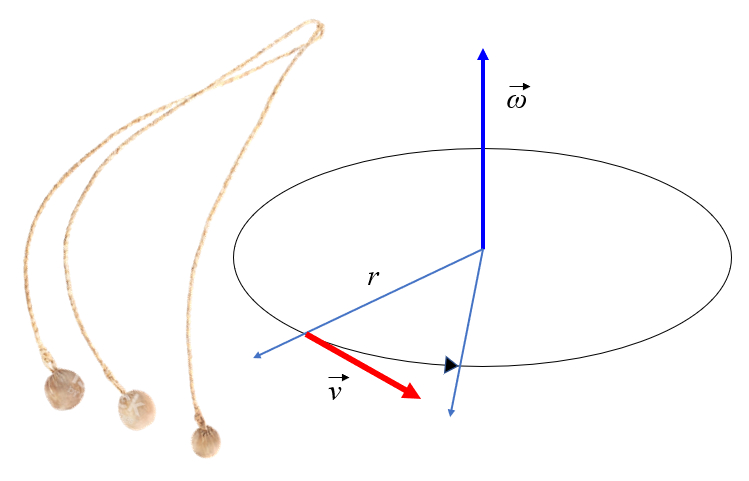
Sin embargo, si se corta el elemento que une el objeto al eje, este continuará moviéndose tangencialmente en línea recta.
ID:(310, 0)
Velocidad angular constante
Descripción 
Para describir la evolución del ángulo en el tiempo, es fundamental analizar su variación a lo largo del mismo. La relación entre la variación del ángulo y el arco recorrido en el tiempo transcurrido es lo que define la velocidad angular. Esta se obtiene al dividir la variación angular por el tiempo transcurrido, dando lugar a la denominada velocidad angular. Cuando se considera un intervalo de tiempo finito, la velocidad angular representa la velocidad angular promedio durante ese período.
Variables
Cálculos
Cálculos
Ecuaciones
En el caso de que la velocidad angular inicial ($\omega_0$) sea igual a la velocidad angular media ($\bar{\omega}$),
| $ \bar{\omega} = \omega_0 $ |
Por lo tanto, con la diferencia de ángulos ($\Delta\theta$), que es igual a el ángulo ($\theta$) dividido por el ángulo inicial ($\theta_0$), obtenemos:
| $ \Delta\theta = \theta_2 - \theta_1 $ |
Y con el tiempo transcurrido ($\Delta t$), que es igual a el tiempo ($t$) dividido por el tiempo inicial ($t_0$), obtenemos:
| $ \Delta t \equiv t - t_0 $ |
Podemos reescribir la ecuaci n de la velocidad angular media ($\bar{\omega}$) como:
| $ \omega_0 \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
Esto se puede expresar como:
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
Despejando, obtenemos:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )$ |
(ID 1023)
Como la velocidad media ($\bar{v}$) es con la distancia recorrida en un tiempo ($\Delta s$) y el tiempo transcurrido ($\Delta t$), igual a
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
y con la distancia recorrida en un tiempo ($\Delta s$) expresado como arco de un c rculo, y el radio ($r$) y la variación del angulo ($\Delta\theta$) son
| $ \Delta s=r \Delta\theta $ |
y la definici n de la velocidad angular media ($\bar{\omega}$) es
| $ \omega_0 \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
entonces,
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Como la relaci n es general, se puede aplicar para valores instant neos, lo que resulta en
| $ v = r \omega $ |
.
(ID 3233)
(ID 3324)
(ID 3324)
La definici n de la velocidad angular media ($\bar{\omega}$) se considera la variación del angulo ($\Delta\theta$),
| $ \Delta\theta = \theta_2 - \theta_1 $ |
y el tiempo transcurrido ($\Delta t$),
| $ \Delta t \equiv t - t_0 $ |
La relaci n entre ambos se define como la velocidad angular media ($\bar{\omega}$):
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
(ID 3679)
Si se parte de la posición inicial ($s_0$) y se desea calcular la distancia recorrida en un tiempo ($\Delta s$), es necesario definir un valor para la posición ($s$).
En un sistema unidimensional, la distancia recorrida en un tiempo ($\Delta s$) se obtiene simplemente restando la posición inicial ($s_0$) de la posición ($s$), lo que da como resultado:
| $ \Delta s = s - s_0 $ |
(ID 4352)
Si un objeto est a una distancia igual a el radio ($r$) de un eje y realiza una rotaci n en una variación del angulo ($\Delta\theta$), que con el ángulo ($\theta$) y el ángulo inicial ($\theta_0$) es
| $ \Delta\theta = \theta_2 - \theta_1 $ |
habr recorrido un arco la distancia recorrida en un tiempo ($\Delta s$), que con la posición ($s$) y la posición inicial ($s_0$) es
| $ \Delta s = s - s_0 $ |
Dicho arco se puede calcular multiplicando el radio ($r$) por el ngulo, es decir,
| $ \Delta s=r \Delta\theta $ |
.
(ID 5302)
Ejemplos
(ID 15409)
Una vez introducido el concepto de tiempo transcurrido, podemos definir el movimiento en t rminos del ngulo recorrido. Para ello, es necesario medir:
• el ngulo actual, que se determina como la diferencia de ngulo con respecto a un origen desde el cual se est midiendo;
• el ngulo inicial, que se determina como la diferencia de ngulo al mismo origen previo, y se calcula como la diferencia entre el primero y el segundo.
(ID 12516)
La base de la descripci n de cualquier evoluci n es la definici n del tiempo en que se describe. En particular, se trabaja con el tiempo transcurrido ($\Delta t$) desde un tiempo de referencia.
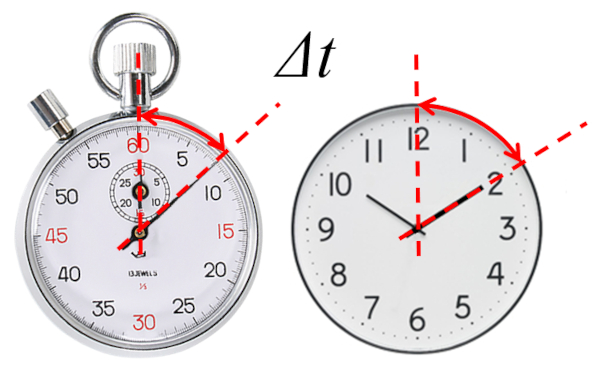
El cronometro nos entre directamente el tiempo transcurrido ya que su tiempo inicial es nulo
En el caso de un cron metro, el tiempo transcurrido se mide desde el inicio de su medici n, es decir, un tiempo inicial cero ($t_0=0$).

En el caso del reloj es necesario definir el tipo inicial para poder determinar el tiempo trascurrido.
En el caso de un reloj, el tiempo transcurrido se mide desde un tiempo inicial definido, que puede ser o no cero.
Como el tiempo transcurrido ($\Delta t$) se calcula como la diferencia entre el tiempo ($t$) y el tiempo inicial ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
es posible "trasladar" el origen del tiempo sumando un valor constante
a ambas magnitudes:
$t \rightarrow t + \tau$
$t_0 \rightarrow t_0 + \tau$
sin afectar el resultado del tiempo transcurrido:
$\Delta t = t - t_0 \rightarrow (t + \tau) - (t_0 + \tau) = t - t_0 = \Delta t$
Este concepto se conoce como invariancia temporal, lo que implica que el valor del tiempo transcurrido no depende del momento espec fico en que se inicia la medici n.
Esto significa que las leyes formuladas utilizando este principio ser n invariantes temporales, es decir, ser n v lidas independientemente de si se aplican en el presente, en el pasado o en el futuro.
(ID 12507)
Una situaci n que puede darse es que la velocidad angular sea constante, lo que significa que el ngulo recorrido crece proporcionalmente al tiempo transcurrido. En otras palabras, con , esto se puede expresar como:
$\omega=\omega_0$
Es importante tener en cuenta que la velocidad angular siempre se mide con respecto a un sistema de referencia. En este caso, la velocidad angular constante se refiere al sistema de referencia en el que se est midiendo.
(ID 11410)
La velocidad angular media se define como el ngulo recorrido en el tiempo transcurrido. Como la rotaci n requiere de un eje, ste se dibuja de forma ortogonal al disco que representa el cuerpo que rota. Para integrar el eje, la velocidad angular se define como un vector en el que la magnitud es el ngulo recorrido por unidad de tiempo y la direcci n se define en funci n de la direcci n del eje:

(ID 10967)
En el caso de velocidad angular constante y conocido el tiempo inicial, el ngulo se puede calcular mediante la siguiente f rmula:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )$ |
La f rmula se representa gr ficamente a continuaci n:
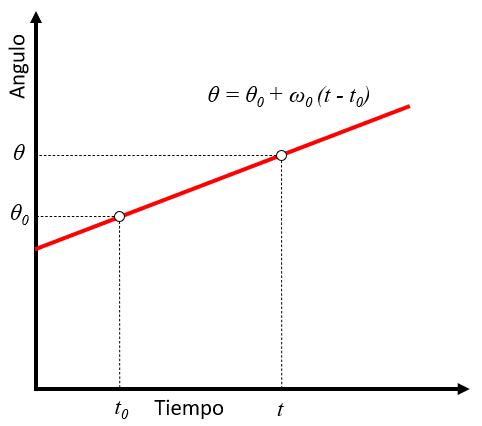
Esta f rmula es til para calcular el ngulo girado por un objeto en situaciones en las que se conoce tanto la velocidad angular como el tiempo inicial. La constancia de la velocidad angular indica que la magnitud de la velocidad angular no cambia con el tiempo. El tiempo inicial es la referencia temporal a partir de la cual se mide el tiempo transcurrido. Por lo tanto, el ngulo girado por el objeto se puede calcular directamente multiplicando la velocidad angular por el tiempo transcurrido desde el tiempo inicial.
(ID 11412)
Si un objeto se somete a un modo de mantener un radio constante, girar como se indica en la figura. Al observar la figura, se notar que la masa realiza un movimiento de traslaci n con una velocidad tangencial que es igual al radio por la velocidad angular:

Sin embargo, si se corta el elemento que une el objeto al eje, este continuar movi ndose tangencialmente en l nea recta.
(ID 310)
La orientaci n de la velocidad tangencial puede ser obtenida utilizando la regla de la mano derecha. Si los dedos se colocan en direcci n del eje de rotaci n y se rotan hacia el vector de posici n (radio), el pulgar apuntar en la direcci n de la velocidad tangencial:
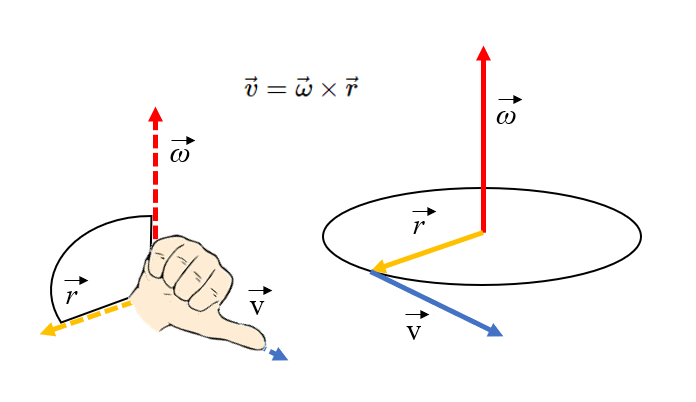
(ID 11599)
(ID 15420)
ID:(611, 0)
