Vitesse angulaire constante
Storyboard 
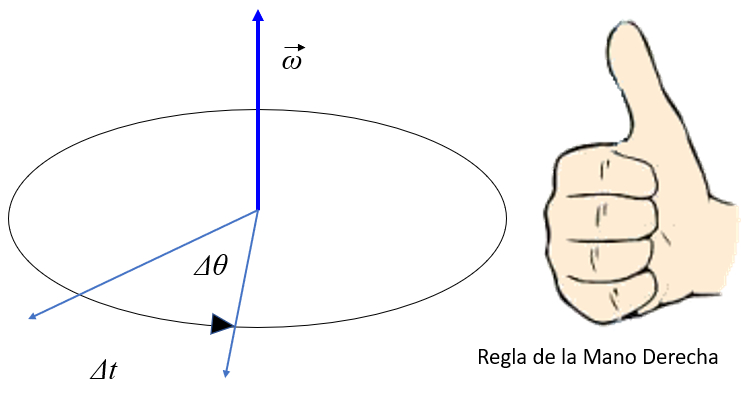
Pour décrire comment l'angle évolue dans le temps, il est nécessaire d'analyser sa variation au fil du temps.
La relation entre la variation de l'angle équivaut à l'angle de l'arc parcouru pendant le temps écoulé, lequel, lorsqu'il est divisé par ce temps, devient la vitesse angulaire.
Lorsque l'on considère un intervalle de temps fini, la vitesse angulaire représente la vitesse angulaire moyenne pendant cette période.
ID:(611, 0)
Angle parcouru
Image 
Une fois le concept de temps écoulé introduit, nous pouvons définir le mouvement en termes d'angle parcouru. Pour ce faire, nous devons mesurer :
• l\'angle actuel, qui est déterminé comme différence d\'angle par rapport à une origine à partir de laquelle nous mesurons ;
• l\'angle initial, qui est déterminé comme différence d\'angle par rapport à la même origine précédente et est calculé comme la différence entre le premier et le second.
ID:(12516, 0)
Vitesse angulaire sous forme graphique
Exercer 
La vitesse angulaire moyenne est définie comme l'angle parcouru pendant le temps écoulé. Comme la rotation nécessite un axe, celui-ci est dessiné de manière orthogonale au disque qui représente le corps en rotation. Pour intégrer l\'axe, la vitesse angulaire est définie comme un vecteur dont la magnitude est l\'angle parcouru par unité de temps et dont la direction est définie en fonction de la direction de l\'axe:
ID:(10967, 0)
Vitesse tangentielle
Script 
Si un objet est soumis à un mode de maintien d'un rayon constant, il tournera comme indiqué dans la figure. En observant la figure, on remarquera que la masse effectue un mouvement de translation avec une vitesse tangentielle égale au rayon multiplié par la vitesse angulaire:
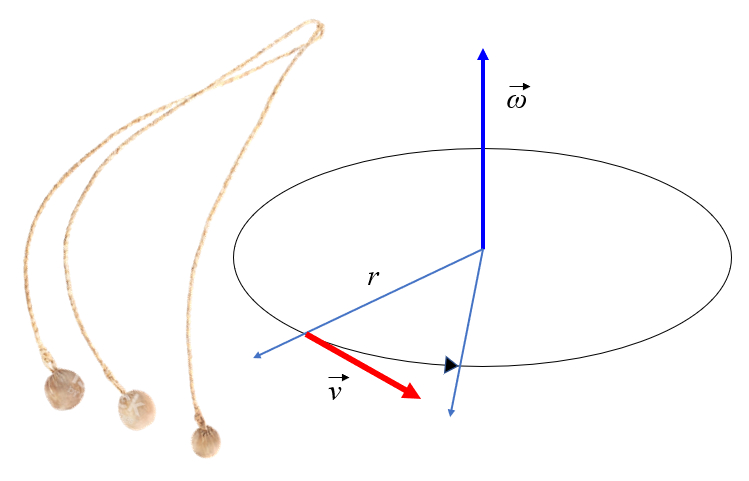
Cependant, si l'élément reliant l\'objet à l\'axe est coupé, l\'objet continuera à se déplacer tangentiellement en ligne droite.
ID:(310, 0)
Vitesse angulaire constante
Description 
Pour décrire comment l'angle évolue dans le temps, il est nécessaire d'analyser sa variation au fil du temps. La relation entre la variation de l'angle équivaut à l'angle de l'arc parcouru pendant le temps écoulé, lequel, lorsqu'il est divisé par ce temps, devient la vitesse angulaire. Lorsque l'on considère un intervalle de temps fini, la vitesse angulaire représente la vitesse angulaire moyenne pendant cette période.
Variables
Calculs
Calculs
Équations
Dans le cas o a vitesse angulaire initiale ($\omega_0$) est gal a vitesse angulaire moyenne ($\bar{\omega}$),
| $ \bar{\omega} = \omega_0 $ |
Par cons quent, avec a différence d'angles ($\Delta\theta$), qui est gal le angle ($\theta$) divis par le angle de départ ($\theta_0$), nous obtenons :
| $ \Delta\theta = \theta_2 - \theta_1 $ |
Et avec le temps écoulé ($\Delta t$), qui est gal le temps ($t$) divis par le temps initial ($t_0$), nous obtenons :
| $ \Delta t \equiv t - t_0 $ |
Nous pouvons r crire l' quation pour a vitesse angulaire moyenne ($\bar{\omega}$) comme suit :
| $ \omega_0 \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
Cela peut tre exprim comme suit :
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
En r solvant cela, nous obtenons :
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )$ |
(ID 1023)
Comme a vitesse moyenne ($\bar{v}$) est avec a distance parcourue en un temps ($\Delta s$) et le temps écoulé ($\Delta t$), gal
| $ v_0 \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
et avec a distance parcourue en un temps ($\Delta s$) exprim comme un arc de cercle, et le radio ($r$) et a variation d'angle ($\Delta\theta$) sont
| $ \Delta s=r \Delta\theta $ |
et la d finition de a vitesse angulaire moyenne ($\bar{\omega}$) est
| $ \omega_0 \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
alors,
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Comme la relation est g n rale, elle peut tre appliqu e pour des valeurs instantan es, ce qui donne
| $ v = r \omega $ |
(ID 3233)
(ID 3324)
(ID 3324)
La d finition de a vitesse angulaire moyenne ($\bar{\omega}$) est consid r e comme a variation d'angle ($\Delta\theta$),
| $ \Delta\theta = \theta_2 - \theta_1 $ |
et le temps écoulé ($\Delta t$),
| $ \Delta t \equiv t - t_0 $ |
La relation entre les deux est d finie comme a vitesse angulaire moyenne ($\bar{\omega}$) :
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
(ID 3679)
Si l’on part de a vitesse ($s_0$) et que l’on souhaite calculer a distance parcourue en un temps ($\Delta s$), il est nécessaire de définir une valeur pour a position ($s$).
Dans un système unidimensionnel, a distance parcourue en un temps ($\Delta s$) est simplement obtenu en soustrayant a vitesse ($s_0$) de a position ($s$), ce qui donne :
| $ \Delta s = s - s_0 $ |
(ID 4352)
Si un objet est une distance gale le radio ($r$) d'un axe et effectue une rotation en une variation d'angle ($\Delta\theta$), ce qui avec le angle ($\theta$) et le angle de départ ($\theta_0$) est
| $ \Delta\theta = \theta_2 - \theta_1 $ |
il aura parcouru un arc a distance parcourue en un temps ($\Delta s$), ce qui avec a position ($s$) et a vitesse ($s_0$) est
| $ \Delta s = s - s_0 $ |
Cet arc peut tre calcul en multipliant le radio ($r$) par l'angle, c'est- -dire
| $ \Delta s=r \Delta\theta $ |
.
(ID 5302)
Exemples
(ID 15409)
Une fois le concept de temps coul introduit, nous pouvons d finir le mouvement en termes d'angle parcouru. Pour ce faire, nous devons mesurer :
• l\'angle actuel, qui est d termin comme diff rence d\'angle par rapport une origine partir de laquelle nous mesurons ;
• l\'angle initial, qui est d termin comme diff rence d\'angle par rapport la m me origine pr c dente et est calcul comme la diff rence entre le premier et le second.
(ID 12516)
La base de la description de toute volution est la d finition du temps auquel elle est d crite. En particulier, on travaille avec le temps écoulé ($\Delta t$) depuis un temps de r f rence.
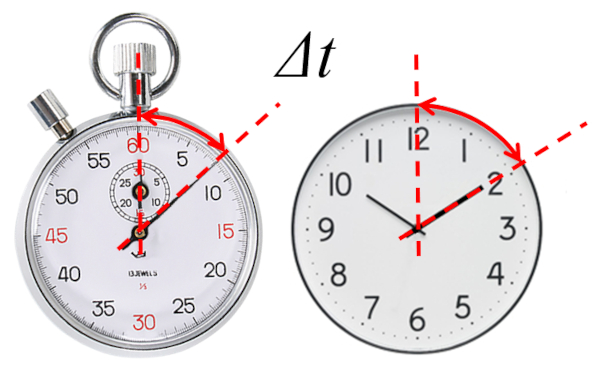
Le chronom tre nous indique directement le temps coul puisque son temps initial est z ro
Dans le cas d'un chronom tre, le temps coul est mesur depuis le d but de sa mesure, c'est- -dire un temps initial nul ($t_0=0$).

Dans le cas de l'horloge, il est n cessaire de d finir le type initial afin de d terminer le temps coul .
Dans le cas d'une montre, le temps coul est mesur depuis un temps initial d fini, qui peut tre nul ou non.
Comme le temps écoulé ($\Delta t$) est calcul comme la diff rence entre le temps ($t$) et le temps initial ($t_0$) :
| $ \Delta t \equiv t - t_0 $ |
il est possible de d placer lorigine du temps en ajoutant une valeur constante
aux deux magnitudes :
$t \rightarrow t + \tau$
$t_0 \rightarrow t_0 + \tau$
sans affecter le r sultat du temps coul :
$\Delta t = t - t_0 \rightarrow (t + \tau) - (t_0 + \tau) = t - t_0 = \Delta t$
Ce concept est appel invariance temporelle, ce qui signifie que la valeur du temps coul ne d pend pas du moment pr cis o commence la mesure.
Cela implique que les lois formul es en utilisant ce principe seront invariantes dans le temps, cest- -dire quelles resteront valides quelles soient appliqu es dans le pr sent, le pass ou le futur.
(ID 12507)
Une situation qui peut se produire est lorsque la vitesse angulaire est constante, ce qui signifie que l'angle parcouru augmente proportionnellement au temps coul . En d'autres termes, en utilisant , cela peut tre exprim comme suit:
$\omega=\omega_0$
Il est important de noter que la vitesse angulaire est toujours mesur e par rapport un syst me de r f rence. Dans ce cas, la vitesse angulaire constante est par rapport au r f rentiel utilis pour la mesure.
(ID 11410)
La vitesse angulaire moyenne est d finie comme l'angle parcouru pendant le temps coul . Comme la rotation n cessite un axe, celui-ci est dessin de mani re orthogonale au disque qui repr sente le corps en rotation. Pour int grer l\'axe, la vitesse angulaire est d finie comme un vecteur dont la magnitude est l\'angle parcouru par unit de temps et dont la direction est d finie en fonction de la direction de l\'axe:

(ID 10967)
Dans le cas d'une vitesse angulaire constante et d\'un temps initial connu, l\'angle peut tre calcul l\'aide de la formule suivante :
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )$ |
La formule est graphiquement repr sent e ci-dessous :

Cette formule est utile pour calculer l\'angle de rotation d\'un objet dans des situations o la fois la vitesse angulaire et le temps initial sont connus. La constance de la vitesse angulaire indique que la magnitude de la vitesse angulaire ne change pas avec le temps. Le temps initial est la r f rence temporelle partir de laquelle le temps coul est mesur . Par cons quent, l\'angle de rotation de l\'objet peut tre calcul directement en multipliant la vitesse angulaire par le temps coul depuis le temps initial.
(ID 11412)
Si un objet est soumis un mode de maintien d'un rayon constant, il tournera comme indiqu dans la figure. En observant la figure, on remarquera que la masse effectue un mouvement de translation avec une vitesse tangentielle gale au rayon multipli par la vitesse angulaire:

Cependant, si l' l ment reliant l\'objet l\'axe est coup , l\'objet continuera se d placer tangentiellement en ligne droite.
(ID 310)
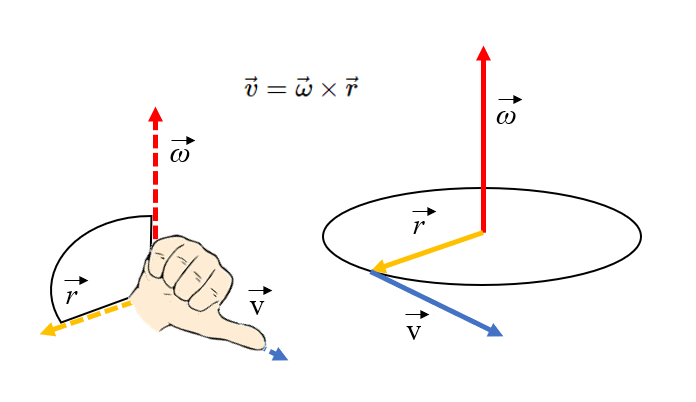
L'orientation de la vitesse tangentielle peut tre obtenue en utilisant la r gle de la main droite. Si les doigts pointent vers l\'axe de rotation et sont ensuite courb s vers le vecteur de position (rayon), le pouce pointera dans la direction de la vitesse tangentielle:
(ID 11599)
(ID 15420)
ID:(611, 0)
