Storyboard

En el caso del resorte la fuerza es proporcional a la elongación del resorte con lo que las ecuaciones de movimiento son lineales y la frecuencia de la oscilación es independiente de la amplitud. Esto es la clave para lograr generar una oscilación que no dependa se que con el roce con el tiempo la amplitud decrezca. Por ello relojes antiguos usaban resortes (circulares) para generar oscilaciones estables para medir el tiempo transcurrido.

>Modelo

ID:(1425, 0)

Ecuación

>Top, >Modelo

La energía cinética de una masa $m$

puede expresarse en función del momento como

$ K =\displaystyle\frac{ p ^2}{2 m_i }$

Condiciones

Variables

$K$

Espacio Momento Posición

$J$

$m_i$

Masa inercial

$kg$

$p$

Momento

$kg m/s$

Relación

Desarrollo

Dado que la energía cinética es igual a

$ K_t =\displaystyle\frac{1}{2} m_i v ^2$

y el momento es

$ p = m_i v $

podemos expresarlo como

$K_t=\displaystyle\frac{1}{2} m_i v^2=\displaystyle\frac{1}{2} m_i \left(\displaystyle\frac{p}{m_i}\right)^2=\displaystyle\frac{p^2}{2m_i}$

es decir,

$ K =\displaystyle\frac{ p ^2}{2 m_i }$

ID:(4425, 0)

Ecuación

>Top, >Modelo

En el caso elástico (resorte) la fuerza es



la energía

se puede mostrar que en este caso es

$ V =\displaystyle\frac{1}{2} k x ^2$

Condiciones

Variables

$k$

Constante de Hooke

$N/m$

$x$

Elongación del resorte

$m$

$V$

Energía potencial

$J$

Relación

Desarrollo

En el caso elástico (resorte) la fuerza es



con k la constante del resorte y x la elongación/compresión del resorte. La variación de la energía potencial es

$ \Delta W = \vec{F} \cdot \Delta\vec{s} $

\\n\\nLa diferencia\\n\\n

$\Delta x = x_2 - x_1$

\\n\\ncorresponde al camino recorrido por lo que\\n\\n

$\Delta W=k,x,\Delta x=k(x_2-x_1)\displaystyle\frac{(x_1+x_2)}{2}=\displaystyle\frac{k}{2}(x_2^2-x_1^2)$

y con ello la energía potencial elástica es

$ V =\displaystyle\frac{1}{2} k x ^2$

ID:(3246, 0)

Ecuación

>Top, >Modelo

Para el caso de una masa oscilando con un resorte, la energía en función del momento $p$ y posición $q$ es

$ E_s =\displaystyle\frac{ p ^2}{2 m_i }+\displaystyle\frac{ k }{2} q ^2$

Condiciones

Variables

$k$

Constante de Hooke

$N/m$

$E_k$

Energía de un sistema con resorte

$J$

$m_i$

Masa inercial

$kg$

$p$

Momento

$kg m/s$

$s$

Posición (vector)

$m$

Relación

Desarrollo

La energía cinética en función del momento está dada por

$ K =\displaystyle\frac{ p ^2}{2 m_i }$

y la energía potencial en función de la altura se expresa como

$ V =\displaystyle\frac{1}{2} k x ^2$

Por lo tanto, si expresamos la elongación como la posición

$x = q$

obtenemos

$ E_s =\displaystyle\frac{ p ^2}{2 m_i }+\displaystyle\frac{ k }{2} q ^2$

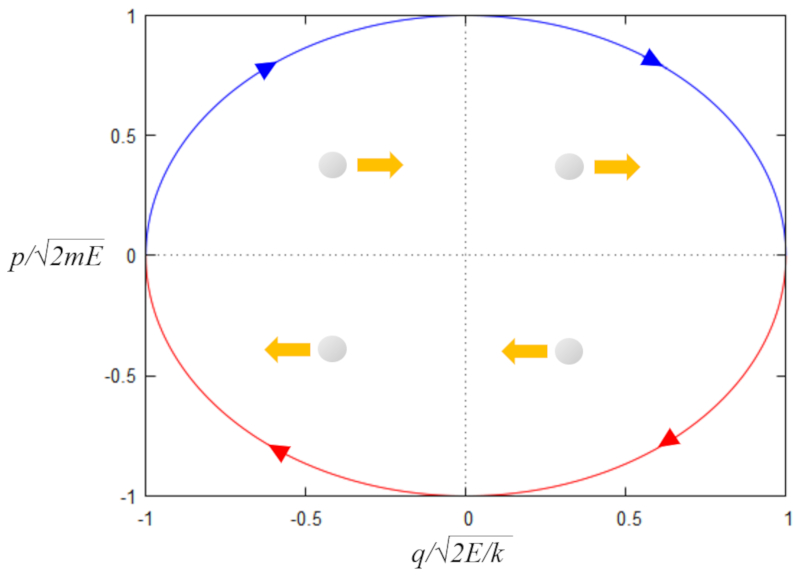
La ecuación puede expresarse en forma adimensional como

$1=y^2 + x^2$

donde

$x=\displaystyle\frac{q}{\sqrt{2E/k}}$

, y

$y=\displaystyle\frac{p}{\sqrt{2m_iE}}$

resolviendo para y, obtenemos

$y=\pm\sqrt{1-x^2}$

Su representación en el plano xy se muestra a continuación

ID:(1187, 0)

Ecuación

>Top, >Modelo

Como la oscilación cumple las leyes físicas se puede hacer uso del hecho que el area debajo de la curva velocidad vs tiempo el camino recorrido para determinar el perido. Como la velocidad es\\n\\n

$\displaystyle\int_0^{T/2}v(t)dt=\sqrt{\displaystyle\frac{2E}{m}}\displaystyle\int_0^{T/2}\cos \displaystyle\frac{2\pi t}{T}dt=\sqrt{\displaystyle\frac{2E}{m}}\displaystyle\frac{T}{\pi}$

\\n\\ny el camino entre un mínimo a un máximo de una elongación, lo que ocurre entre el tiempo 0 y T/2 es igual a\\n\\n

$x_{max}-x_{min}=2\sqrt{\displaystyle\frac{2E}{k}}$

se tiene que

$ T =2 \pi \sqrt{\displaystyle\frac{ m_i }{ k }}$

Condiciones

Variables

$k$

Constante de Hooke

$N/m$

$m_i$

Masa inercial

$kg$

$T$

Período

$s$

$\pi$

Pi

3.1415927

$rad$

Relación

ID:(7106, 0)

Ecuación

>Top, >Modelo

Uno de los sistemas que ilustra es el de un resorte. Este se relaciona con la deformación elástica del material del que está compuesto el resorte. Cuando hablamos de "elástica", nos referimos a una deformación que, al eliminar la tensión aplicada, permite que el sistema recupere completamente su forma original. Se entiende que no sufre una deformación plástica.

Dado que la energía del resorte está dada por

$E=\displaystyle\frac{1}{2}m_i v^2+\displaystyle\frac{1}{2}k x^2$

el período será igual a

$T=2\pi\sqrt{\displaystyle\frac{m_i}{k}}$

y, por lo tanto, la frecuencia angular es

$ \omega_0 ^2=\displaystyle\frac{ k }{ m_i }$

Condiciones

Variables

$k$

Constante de Hooke

$N/m$

$\omega_0$

Frecuencia angular del resorte

$rad/s$

$m_i$

Masa inercial

$kg$

Relación

Desarrollo

Dado que la energía cinética depende de la masa $m$ y la velocidad $v$, se tiene que

$ K_t =\displaystyle\frac{1}{2} m_i v ^2$

y la energía potencial del resorte, que depende de la constante de elasticidad $k$ y la elongación $x$, es

$ V =\displaystyle\frac{1}{2} k x ^2$

Por lo tanto, la energía total se expresa como

$E=\displaystyle\frac{1}{2}m_i v^2+\displaystyle\frac{1}{2}k x^2$

Dado que el período es

$T=2\pi\sqrt{\displaystyle\frac{m_i}{k}}$

podemos calcular la frecuencia angular como

$\omega_0=\displaystyle\frac{2\pi}{T}=\sqrt{\displaystyle\frac{k}{m_i}}$

lo que significa que

$ \omega_0 ^2=\displaystyle\frac{ k }{ m_i }$

ID:(1242, 0)

0

Video

Video: Osciladores de un resorte