Druyd:Knowledge

Oscilación de un Péndulo

Storyboard

Al no ser el torque proporcional al angulo la frecuencia de oscilación depende de la amplitud lo que dificulta su aplicación para marcar el paso en un reloj. Sin embargo el efecto es mínimo si el angulo es pequeño lo que lleva a que la aplicación del péndulo en relojes se logra con barras largas.

>Modelo

ID:(1426, 0)

Calculo de la energía potencial del péndulo

Definición

Cuando se desvía un péndulo de longitud $l$ en un ángulo $\theta$ , la masa gana altura, que se calcula como

$l - l \cos\theta = l (1 - \cos\theta)$

esto se relaciona con la ganancia de energía potencial gravitatoria.

ID:(1239, 0)

Oscilación de un Péndulo

Descripción

En el caso de un péndulo es la gravedad la que genera un torque opuesto a que la masa abandone el punto de reposo. Sin embargo el torque no es proporcional al angulo existiendo una relación no lineal lo que hace mas complejo el movimiento. Al no ser el torque proporcional al angulo la frecuencia de oscilación depende de la amplitud lo que dificulta su aplicación para marcar el paso en un reloj. Sin embargo el efecto es mínimo si el angulo es pequeño lo que lleva a que la aplicación del péndulo en relojes se logra con barras largas.

Variables

Símbolo

Texto

Variable

Valor

Unidades

Calcule

Valor MKS

Unidades MKS

$h$

Altura en el caso del péndulo

$\theta$

theta

Angulo de oscilación

rad

$V$

Energía potencial del péndulo

$V$

Energía potencial del péndulo, para ángulos pequeños

$L$

Largo del péndulo

$m_g$

m_g

Masa gravitacional

Cálculos

Ecuación

Número

Primero, seleccione la ecuación:

, luego, seleccione la variable:

Símbolo

Ecuación

Resuelto

Traducido

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

Variable

Dado

Calcule

Objetivo :

Ecuación

A utilizar

Ecuaciones

$U = m g L (1-\cos \theta )$

U = m * g * L *(1-cos( theta ))

(ID 4513)

$V =\displaystyle\frac{1}{2} m_g g L \theta ^2$

V = m_g * g * L * theta ^2/2

La energ a potencial gravitacional de un p ndulo con masa m, suspendido de un hilo de longitud L y desviado por un ngulo \theta es

$U = m g L (1-\cos \theta )$

donde g es la aceleraci n debida a la gravedad.

Para peque os ngulos, la funci n coseno se puede aproximar mediante la serie de Taylor hasta el segundo t rmino

$\cos\theta\sim 1-\displaystyle\frac{1}{2}\theta^2$

lo que lleva a que la energ a potencial se reduce a

$V =\displaystyle\frac{1}{2} m_g g L \theta ^2$

(ID 4514)

$h = L (1-\cos \theta )$

h = L * (1-cos( theta ))

(ID 4523)

Ejemplos

Calculo de la energ a potencial del p ndulo

Cuando se desv a un p ndulo de longitud $l$ en un ngulo $\theta$ , la masa gana altura, que se calcula como

$l - l \cos\theta = l (1 - \cos\theta)$

esto se relaciona con la ganancia de energ a potencial gravitatoria.

(ID 1239)

Altura del centro de masa en un p ndulo

Para un p ndulo de longitud $L$ que se desv a en un ngulo $\theta$ , la masa se eleva

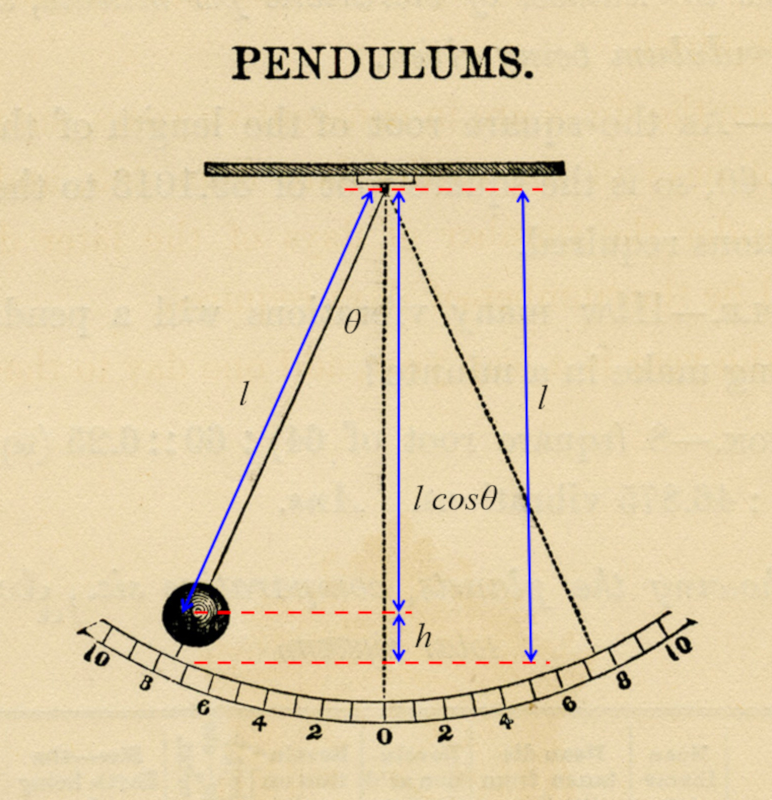
a una altura igual a:

$h = L (1-\cos \theta )$

(ID 4523)

Energ a potencial de un p ndulo matem tico

Para el caso de una masa $m$ que cuelga de un hilo de longitud $L$ y es desviada en un ngulo $\theta$ respecto a la vertical, la masa ganar una altura de

$h = L (1-\cos \theta )$

lo que implica que la energ a potencial gravitacional

$V = - m_g g z$

ser

$U = m g L (1-\cos \theta )$

donde $g$ es la aceleraci n debida a la gravedad.

(ID 4513)

Energ a potencial de un p ndulo matem tico para peque os ngulos

La energ a potencial gravitacional de un p ndulo es

$U = m g L (1-\cos \theta )$

que para ngulos peque os puede aproximarse como:

$V =\displaystyle\frac{1}{2} m_g g L \theta ^2$

Es importante destacar que el ngulo debe estar expresado en radianes.

(ID 4514)

ID:(1426, 0)