Fluxo de um líquido incompressível
Storyboard 
Quando um líquido está em movimento, chamamos isso de fluxo, e sua medida é baseada no volume que passa por uma seção em um determinado período de tempo. Supondo que o volume se desloque sem deformação, a velocidade com que o líquido passa pela seção permanece constante. Nesse contexto, o fluxo também pode ser definido como o produto da velocidade e da área da seção transversal.
ID:(875, 0)
Fluxo de um líquido incompressível
Storyboard 
Quando um líquido está em movimento, chamamos isso de fluxo, e sua medida é baseada no volume que passa por uma seção em um determinado período de tempo. Supondo que o volume se desloque sem deformação, a velocidade com que o líquido passa pela seção permanece constante. Nesse contexto, o fluxo também pode ser definido como o produto da velocidade e da área da seção transversal.
Variáveis
Cálculos
Cálculos
Equações
O fluxo definido como o volume o elemento de volume ($\Delta V$) dividido pelo tempo o tempo decorrido ($\Delta t$), conforme expresso na seguinte equa o:
e o volume igual rea da se o la seção de tubo ($S$) multiplicada pela dist ncia percorrida o elemento de tubo ($\Delta s$):
Como a dist ncia percorrida o elemento de tubo ($\Delta s$) por unidade de tempo o tempo decorrido ($\Delta t$) corresponde velocidade, ela representada por:
Assim, o fluxo uma densidade de fluxo ($j_s$), que calculado usando:
O fluxo definido como o volume o elemento de volume ($\Delta V$) dividido pelo tempo o tempo decorrido ($\Delta t$), conforme expresso na seguinte equa o:
e o volume igual rea da se o la seção de tubo ($S$) multiplicada pela dist ncia percorrida o elemento de tubo ($\Delta s$):
Como a dist ncia percorrida o elemento de tubo ($\Delta s$) por unidade de tempo o tempo decorrido ($\Delta t$) corresponde velocidade, ela representada por:
Assim, o fluxo uma densidade de fluxo ($j_s$), que calculado usando:
Exemplos
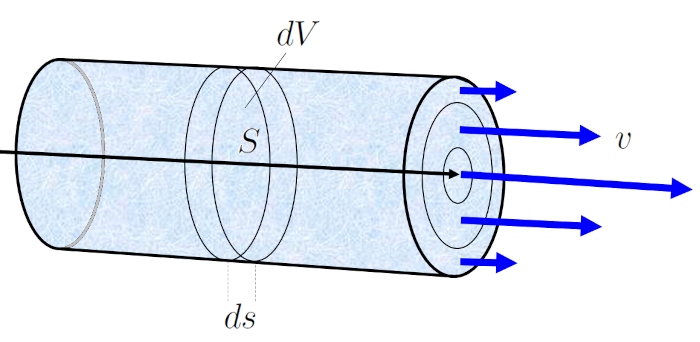
Durante um tempo decorrido ($\Delta t$), o fluido com uma velocidade média do fluido ($v$) se desloca um elemento de tubo ($\Delta s$). Se la seção ($S$) representa a quantidade de fluido que atravessa essa se o em o tempo decorrido ($\Delta t$), calculada como:
$\Delta V = S \Delta s = Sv \Delta t$
Esta equa o indica que o volume de fluido que flui atrav s da se o la seção ($S$) durante um tempo decorrido ($\Delta t$) igual ao produto da rea da se o e a dist ncia percorrida pelo fluido nesse tempo.
Isso facilita o c lculo de o elemento de volume ($\Delta V$), que o volume de fluido que flui pelo canal em um per odo espec fico de o tempo decorrido ($\Delta t$), correspondente a o fluxo de volume ($J_V$).
O fluxo definido como o volume o elemento de volume ($\Delta V$) dividido pelo tempo o tempo decorrido ($\Delta t$), conforme expresso na seguinte equa o:
e o volume igual rea da se o la seção de tubo ($S$) multiplicada pela dist ncia percorrida o elemento de tubo ($\Delta s$):
Como a dist ncia percorrida o elemento de tubo ($\Delta s$) por unidade de tempo o tempo decorrido ($\Delta t$) corresponde velocidade, ela representada por:
Assim, o fluxo uma densidade de fluxo ($j_s$), que calculado usando:
importante destacar que neste modelo:
A densidade de fluxo funciona como uma velocidade m dia em toda a se o do fluxo.
Considerando um tubo que n o vaza nem recebe l quido adicional, o fluxo que entra em um ponto 1 O fluxo de volume 1 ($J_{V1}$) ser igual ao fluxo que sai em um ponto 2 O fluxo de volume 2 ($J_{V2}$):
Dentro de um canal ou tubo, pode haver uma mudan a na rea de se o transversal, seja ela alargando ou estreitando.
Essa varia o afetar diretamente o fluxo atrav s de la densidade de fluxo ($j_s$), que representa a velocidade, aumentando (se a se o estreita) ou diminuindo (se amplia) de acordo com la seção de tubo ($S$) para manter o fluxo de volume ($J_V$) constante, conforme indicado pela:
A conserva o do fluxo, juntamente com a defini o de densidade de fluxo, leva lei de conserva o, de modo que la seção no ponto 1 ($S_1$), la seção no ponto 2 ($S_2$), la densidade de fluxo 1 ($j_{s1}$) e la densidade de fluxo 2 ($j_{s2}$) satisfazem:
A equa o de continuidade pressup e que o fluxo seja uniforme, sem fluxos reversos ou turbul ncias presentes. Portanto, necess rio verificar se o fluxo realmente laminar e livre de turbul ncias, especialmente ao aplicar a equa o para analisar o fluxo de fluidos em tubos e canais.
Existem v rios m todos para detectar turbul ncias no fluxo, como o uso de medidores de fluxo ou observa o visual do fluxo. essencial garantir que o fluxo seja est vel antes de aplicar a equa o de continuidade, pois qualquer perturba o no fluxo pode afetar a precis o dos c lculos e a efici ncia geral do sistema.
Se tivermos um tubo com uma la seção de tubo ($S$) que se desloca uma dist ncia de o elemento de tubo ($\Delta s$) ao longo do seu eixo, tendo deslocado o elemento de volume ($\Delta V$), ent o igual a:
Se tivermos um tubo com uma la seção de tubo ($S$) que se desloca uma dist ncia de o elemento de tubo ($\Delta s$) ao longo do seu eixo, tendo deslocado o elemento de volume ($\Delta V$), ent o igual a:
O fluxo de volume ($J_V$) corresponde a o volume de fluxo ($\Delta V$) que flui atrav s do canal em o tempo decorrido ($\Delta t$). Portanto, temos:
O fluxo de volume ($J_V$) corresponde a o volume de fluxo ($\Delta V$) que flui atrav s do canal em o tempo decorrido ($\Delta t$). Portanto, temos:
La densidade de fluxo ($j_s$) est relacionado com la distância percorrida em um tempo ($\Delta s$), que a dist ncia que o fluido percorre em o tempo decorrido ($\Delta t$), da seguinte maneira:
La densidade de fluxo ($j_s$) est relacionado com la distância percorrida em um tempo ($\Delta s$), que a dist ncia que o fluido percorre em o tempo decorrido ($\Delta t$), da seguinte maneira:
Uma densidade de fluxo ($j_s$) pode ser expresso em termos de o fluxo de volume ($J_V$) utilizando la seção ou superfície ($S$) atrav s da seguinte f rmula:
Uma densidade de fluxo ($j_s$) pode ser expresso em termos de o fluxo de volume ($J_V$) utilizando la seção ou superfície ($S$) atrav s da seguinte f rmula:
Uma das leis mais b sicas na f sica a conserva o da massa, que v lida em todo o nosso mundo macrosc pico. Apenas no mundo microsc pico existe uma convers o entre massa e energia, a qual n o consideraremos neste caso. No caso de um fluido, isso significa que a massa que entra por um tubo deve ser igual que sai dele.
Se a densidade for constante, o mesmo se aplica ao volume. Nestes casos, quando tratamos o fluxo como um fluido incompress vel, significa que um determinado volume que entra em uma extremidade do tubo deve sair pela outra extremidade. Isso pode ser expresso como a igualdade entre o fluxona posição 1 ($J_1$) e o fluxona posição 2 ($J_2$), com a equa o:
La superfície de um disco ($S$) de um raio do disco ($r$) calculada da seguinte forma:
La superfície de um disco ($S$) de um raio do disco ($r$) calculada da seguinte forma:
O princ pio da continuidade determina que o fluxo no primeiro ponto, que igual a la densidade de fluxo 1 ($j_{s1}$) vezes la seção no ponto 1 ($S_1$), deve ser igual ao fluxo no segundo ponto, dado por la densidade de fluxo 2 ($j_{s2}$) vezes la seção no ponto 2 ($S_2$). A partir disso, conclui-se que:
ID:(875, 0)