Benützer:
Strömung einer inkompressiblen Flüssigkeit
Storyboard 
Wenn eine Flüssigkeit sich bewegt, sprechen wir von einem Fluss. Ihre Messung basiert auf dem Volumen, das innerhalb einer bestimmten Zeitspanne eine bestimmte Querschnittsfläche durchquert. Wenn wir davon ausgehen, dass das Volumen ohne Verformung bewegt wird, bleibt die Geschwindigkeit, mit der die Flüssigkeit die Querschnittsfläche durchquert, konstant. In diesem Fall kann der Fluss auch als das Produkt aus Geschwindigkeit und Querschnittsfläche definiert werden.
ID:(875, 0)
Volumenstrom
Konzept
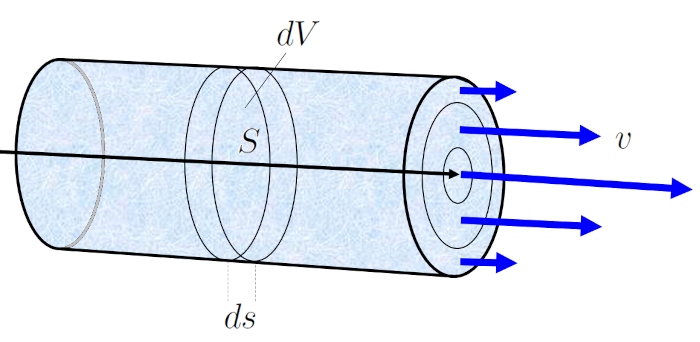
Während ein Abgelaufene Zeit ($\Delta t$) bewegt sich die Flüssigkeit mit eine Mittlere Geschwindigkeit der Flüssigkeit ($v$) um ein Rohrelement ($\Delta s$). Wenn die Abschnitt ($S$) die Menge an Flüssigkeit darstellt, die in der Abgelaufene Zeit ($\Delta t$) diesen Abschnitt durchquert, wird sie wie folgt berechnet:
$\Delta V = S \Delta s = Sv \Delta t$
Diese Gleichung besagt, dass das Volumen der Flüssigkeit, das während ein Abgelaufene Zeit ($\Delta t$) durch den Abschnitt die Abschnitt ($S$) fließt, gleich dem Produkt aus der Querschnittsfläche und der zurückgelegten Distanz der Flüssigkeit in dieser Zeit ist.
Dies erleichtert die Berechnung von der Volumenelement ($\Delta V$), dem Volumen der Flüssigkeit, das in einem bestimmten Zeitraum von der Abgelaufene Zeit ($\Delta t$) durch den Kanal fließt, entsprechend der Volumenstrom ($J_V$).
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
ID:(2212, 0)
Volumenstrom und seine Geschwindigkeit
Konzept
Der Fluss wird als das Volumen der Volumenelement ($\Delta V$) geteilt durch die Zeit der Abgelaufene Zeit ($\Delta t$) definiert, was durch die folgende Gleichung ausgedrückt wird:
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
und das Volumen ist das Produkt der Querschnittsfläche die Rohr Sektion ($S$) mit dem zurückgelegten Weg der Rohrelement ($\Delta s$):
| $ \Delta V = S \Delta s $ |
Da der zurückgelegte Weg der Rohrelement ($\Delta s$) pro Zeiteinheit der Abgelaufene Zeit ($\Delta t$) der Geschwindigkeit entspricht, wird dies durch die folgende Gleichung dargestellt:
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Somit ist der Fluss eine Flussdichte ($j_s$), der mit der folgenden Gleichung berechnet wird:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Es ist wichtig zu beachten, dass in diesem Modell:
Die Flussdichte als durchschnittliche Geschwindigkeit über den gesamten Querschnitt des Flusses wirkt.
ID:(15715, 0)
Kanal mit variablem Querschnitt
Konzept
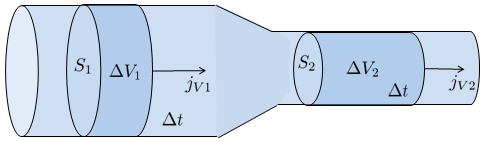
Unter der Annahme, dass ein Rohr weder leckt noch Flüssigkeit hinzugefügt wird, ist der Fluss, der an einem Punkt 1 Der Volumenstrom 1 ($J_{V1}$) eintritt, gleich dem Fluss, der an einem Punkt 2 Der Volumenstrom 2 ($J_{V2}$) austritt:
| $ J_{V1} = J_{V2} $ |
Innerhalb eines Kanals oder Rohres kann es zu einer Änderung des Querschnitts kommen, entweder durch Erweiterung oder Verengung.
Diese Veränderung wird den Fluss durch die Flussdichte ($j_s$), welcher die Geschwindigkeit repräsentiert, direkt beeinflussen, indem sie zunimmt (wenn sich der Abschnitt verengt) oder abnimmt (wenn er sich erweitert), entsprechend die Rohr Sektion ($S$), um der Volumenstrom ($J_V$) konstant zu halten, wie durch die Gleichung angegeben:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Die Erhaltung des Flusses zusammen mit der Definition der Flussdichte führt zu einem Erhaltungsgesetz, so dass die Abschnitt in Punkt 1 ($S_1$), die Abschnitt in Punkt 2 ($S_2$), die Flussdichte 1 ($j_{s1}$) und die Flussdichte 2 ($j_{s2}$) erfüllen:
| $ S_1 j_{s1} = S_2 j_{s2} $ |
ID:(2213, 0)
Gültigkeit der Kontinuitätsgleichung
Konzept
Die Kontinuitätsgleichung setzt voraus, dass der Fluss gleichmäßig ist und keine Rückflüsse oder Turbulenzen auftreten. Daher ist es notwendig sicherzustellen, dass der Fluss tatsächlich laminar ist und keine Turbulenzen aufweist, insbesondere wenn die Gleichung zur Analyse von Fluidströmungen in Rohren und Kanälen verwendet wird.
Es gibt verschiedene Methoden zur Erkennung von Turbulenzen im Fluss, wie die Verwendung von Durchflussmessern oder die visuelle Beobachtung des Flusses. Es ist unerlässlich, sicherzustellen, dass der Fluss stabil ist, bevor die Kontinuitätsgleichung angewendet wird, da jede Störung im Fluss die Genauigkeit der Berechnungen und die Gesamteffizienz des Systems beeinträchtigen kann.
ID:(978, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ \Delta V_1 = S_1 \Delta s_1 $
DV = S * Ds
$ \Delta V_2 = S_2 \Delta s_2 $
DV = S * Ds
$ j_{s1} =\displaystyle\frac{ \Delta s_1 }{ \Delta t }$
j_s = Ds / Dt
$ j_{s2} =\displaystyle\frac{ \Delta s_2 }{ \Delta t }$
j_s = Ds / Dt
$ j_{s1} = \displaystyle\frac{ J_{V1} }{ S_1 }$
j_s = J_V / S
$ j_{s2} = \displaystyle\frac{ J_{V2} }{ S_2 }$
j_s = J_V / S
$ J_{V1} =\displaystyle\frac{ \Delta V_1 }{ \Delta t }$
J_V = DV / Dt
$ J_{V2} =\displaystyle\frac{ \Delta V_2 }{ \Delta t }$
J_V = DV / Dt
$ J_{V1} = J_{V2} $
J_V1 = J_V2
$ S_1 = \pi r_1 ^2$
S = pi * r ^2
$ S_2 = \pi r_2 ^2$
S = pi * r ^2
$ S_1 j_{s1} = S_2 j_{s2} $
S_1 * j_s1 = S_2 * j_s2
ID:(15488, 0)
Volumenelement (1)
Gleichung
Wenn wir ein Rohr mit einer die Rohr Sektion ($S$) haben, das eine Strecke von der Rohrelement ($\Delta s$) entlang seiner Achse bewegt hat, nachdem es der Volumenelement ($\Delta V$) verschoben wurde, dann ist es gleich:
| $ \Delta V_1 = S_1 \Delta s_1 $ |
| $ \Delta V = S \Delta s $ |
ID:(3469, 1)
Volumenelement (2)
Gleichung
Wenn wir ein Rohr mit einer die Rohr Sektion ($S$) haben, das eine Strecke von der Rohrelement ($\Delta s$) entlang seiner Achse bewegt hat, nachdem es der Volumenelement ($\Delta V$) verschoben wurde, dann ist es gleich:
| $ \Delta V_2 = S_2 \Delta s_2 $ |
| $ \Delta V = S \Delta s $ |
ID:(3469, 2)
Mittlerer Volumenstrom (1)
Gleichung
Der Volumenstrom ($J_V$) entspricht der Volume Fließende ($\Delta V$), das durch den Kanal bei der Abgelaufene Zeit ($\Delta t$) fließt. Daher haben wir:
| $ J_{V1} =\displaystyle\frac{ \Delta V_1 }{ \Delta t }$ |
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
ID:(4347, 1)
Mittlerer Volumenstrom (2)
Gleichung
Der Volumenstrom ($J_V$) entspricht der Volume Fließende ($\Delta V$), das durch den Kanal bei der Abgelaufene Zeit ($\Delta t$) fließt. Daher haben wir:
| $ J_{V2} =\displaystyle\frac{ \Delta V_2 }{ \Delta t }$ |
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
ID:(4347, 2)
Durchschnittliche Strömungsdichte (1)
Gleichung
Die Flussdichte ($j_s$) steht in Beziehung zu die Zurückgelegte Strecke in einer Zeit ($\Delta s$), was die Strecke ist, die die Flüssigkeit in der Abgelaufene Zeit ($\Delta t$) zurücklegt, wie folgt:
| $ j_{s1} =\displaystyle\frac{ \Delta s_1 }{ \Delta t }$ |
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
ID:(4348, 1)
Durchschnittliche Strömungsdichte (2)
Gleichung
Die Flussdichte ($j_s$) steht in Beziehung zu die Zurückgelegte Strecke in einer Zeit ($\Delta s$), was die Strecke ist, die die Flüssigkeit in der Abgelaufene Zeit ($\Delta t$) zurücklegt, wie folgt:
| $ j_{s2} =\displaystyle\frac{ \Delta s_2 }{ \Delta t }$ |
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
ID:(4348, 2)
Volumenstrom und seine Geschwindigkeit (1)
Gleichung
Eine Flussdichte ($j_s$) kann in Bezug auf der Volumenstrom ($J_V$) durch die Abschnitt oder Bereich ($S$) mit der folgenden Formel dargestellt werden:
| $ j_{s1} = \displaystyle\frac{ J_{V1} }{ S_1 }$ |
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Der Fluss wird als das Volumen der Volumenelement ($\Delta V$) geteilt durch die Zeit der Abgelaufene Zeit ($\Delta t$) definiert, was durch die folgende Gleichung ausgedrückt wird:
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
und das Volumen ist das Produkt der Querschnittsfläche die Rohr Sektion ($S$) mit dem zurückgelegten Weg der Rohrelement ($\Delta s$):
| $ \Delta V = S \Delta s $ |
Da der zurückgelegte Weg der Rohrelement ($\Delta s$) pro Zeiteinheit der Abgelaufene Zeit ($\Delta t$) der Geschwindigkeit entspricht, wird dies durch die folgende Gleichung dargestellt:
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Somit ist der Fluss eine Flussdichte ($j_s$), der mit der folgenden Gleichung berechnet wird:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
ID:(4349, 1)
Volumenstrom und seine Geschwindigkeit (2)
Gleichung
Eine Flussdichte ($j_s$) kann in Bezug auf der Volumenstrom ($J_V$) durch die Abschnitt oder Bereich ($S$) mit der folgenden Formel dargestellt werden:
| $ j_{s2} = \displaystyle\frac{ J_{V2} }{ S_2 }$ |
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Der Fluss wird als das Volumen der Volumenelement ($\Delta V$) geteilt durch die Zeit der Abgelaufene Zeit ($\Delta t$) definiert, was durch die folgende Gleichung ausgedrückt wird:
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
und das Volumen ist das Produkt der Querschnittsfläche die Rohr Sektion ($S$) mit dem zurückgelegten Weg der Rohrelement ($\Delta s$):
| $ \Delta V = S \Delta s $ |
Da der zurückgelegte Weg der Rohrelement ($\Delta s$) pro Zeiteinheit der Abgelaufene Zeit ($\Delta t$) der Geschwindigkeit entspricht, wird dies durch die folgende Gleichung dargestellt:
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Somit ist der Fluss eine Flussdichte ($j_s$), der mit der folgenden Gleichung berechnet wird:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
ID:(4349, 2)
Volumen Erhaltung
Gleichung
Eine der grundlegendsten Gesetze in der Physik ist die Erhaltung der Masse, die in unserer makroskopischen Welt gilt. Nur in der mikroskopischen Welt existiert eine Umwandlung zwischen Masse und Energie, die wir in diesem Fall nicht berücksichtigen werden. Im Falle eines Fluids bedeutet dies, dass die Masse, die durch ein Rohr eintritt, gleich der Masse sein muss, die es verlässt.
Wenn die Dichte konstant ist, gilt dasselbe für das Volumen. In solchen Fällen, wenn wir den Fluss als ein inkompressibles Fluid behandeln, bedeutet dies, dass ein bestimmtes Volumen, das an einem Ende des Rohrs eintritt, am anderen Ende austreten muss. Dies kann als Gleichheit zwischen der Fließen in Position 1 ($J_1$) und der Fließen in Position 2 ($J_2$) ausgedrückt werden, mit der Gleichung:
| $ J_{V1} = J_{V2} $ |
ID:(939, 0)
Oberfläche einer Scheibe (1)
Gleichung
Die Oberfläche einer Scheibe ($S$) von ein Scheibenradius ($r$) wird wie folgt berechnet:
| $ S_1 = \pi r_1 ^2$ |
| $ S = \pi r ^2$ |
ID:(3804, 1)
Oberfläche einer Scheibe (2)
Gleichung
Die Oberfläche einer Scheibe ($S$) von ein Scheibenradius ($r$) wird wie folgt berechnet:
| $ S_2 = \pi r_2 ^2$ |
| $ S = \pi r ^2$ |
ID:(3804, 2)
Kontinuität nach Abschnitten
Gleichung
Das Kontinuitätsprinzip besagt, dass der Fluss am ersten Punkt, der gleich die Flussdichte 1 ($j_{s1}$) mal die Abschnitt in Punkt 1 ($S_1$) ist, dem Fluss am zweiten Punkt entsprechen muss, der durch die Flussdichte 2 ($j_{s2}$) mal die Abschnitt in Punkt 2 ($S_2$) gegeben ist. Daraus folgt:
| $ S_1 j_{s1} = S_2 j_{s2} $ |
ID:(4350, 0)