Dos placa con cargas opuestas
Storyboard 
La geometría conocida como placas paralelas se puede describir como dos planos infinitos que está cargado eléctricamente con cargas iguales y opuestas.
ID:(2076, 0)
Dos placa con cargas opuestas
Storyboard 
La geometría conocida como placas paralelas se puede describir como dos planos infinitos que está cargado eléctricamente con cargas iguales y opuestas.
Variables
Cálculos
Cálculos
Ecuaciones
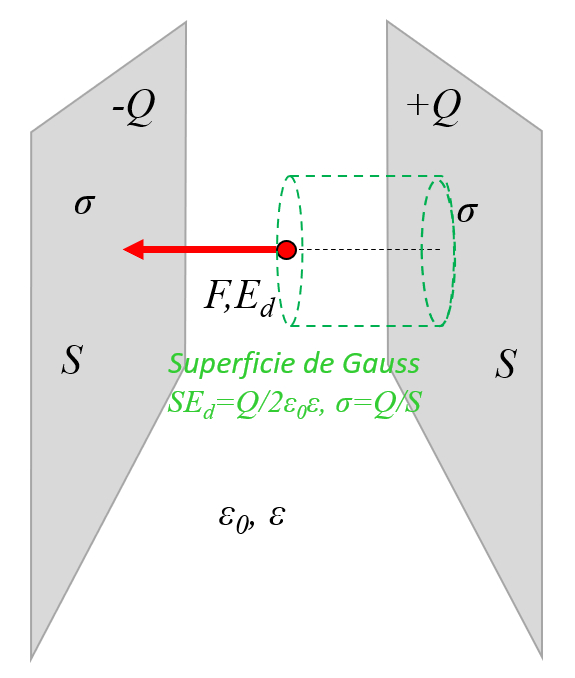
En el caso de una superficie gaussiana plana, el campo eléctrico ($\vec{E}$) es constante en la direcci n de el versor normal a la sección ($\hat{n}$). Por lo tanto, utilizando las variables la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$) y la constante dieléctrica ($\epsilon$), se puede calcular integrando sobre la superficie en que campo eléctrico es constante ($dS$):
Adem s, la densidad de carga por área ($\sigma$) se calcula utilizando la superficie ($S$) y la carga ($Q$) seg n la siguiente ecuaci n:
Por lo tanto, se concluye que el campo eléctrico, dos placas infinitas ($E_d$) es:
El potencial eléctrico, dos placas infinitas ($\varphi_d$) en relaci n con el campo eléctrico, dos placas infinitas ($E_d$) y la posición en el eje z ($z$) se expresa como:
De manera similar, el campo eléctrico, dos placas infinitas ($E_d$) en relaci n con la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$) y la densidad de carga por área ($\sigma$) se define como:
Integrando desde el origen, obtenemos:
$\varphi_d = -\displaystyle\int_0^z du \displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon }= -\displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon } z$
Por lo tanto, el potencial eléctrico, dos placas infinitas ($\varphi_d$) resulta en:
El potencial eléctrico, dos placas infinitas ($\varphi_d$) en relaci n con el campo eléctrico, dos placas infinitas ($E_d$) y la posición en el eje z ($z$) se expresa como:
De manera similar, el campo eléctrico, dos placas infinitas ($E_d$) en relaci n con la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$) y la densidad de carga por área ($\sigma$) se define como:
Integrando desde el origen, obtenemos:
$\varphi_d = -\displaystyle\int_0^z du \displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon }= -\displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon } z$
Por lo tanto, el potencial eléctrico, dos placas infinitas ($\varphi_d$) resulta en:
Ejemplos
En el caso de una superficie gaussiana plana, el campo eléctrico ($\vec{E}$) es constante en la direcci n de el versor normal a la sección ($\hat{n}$). Por lo tanto, utilizando las variables la carga ($Q$), la constante de campo eléctrico ($\epsilon_0$) y la constante dieléctrica ($\epsilon$), se puede calcular integrando sobre la superficie en que campo eléctrico es constante ($dS$):
lo que se muestra en la grafica
Adem s, la densidad de carga por área ($\sigma$) se calcula utilizando la superficie ($S$) y la carga ($Q$) seg n la siguiente ecuaci n:
Por lo tanto, se concluye que el campo eléctrico, dos placas infinitas ($E_d$) es:
El potencial eléctrico, dos placas infinitas ($\varphi_d$) en relaci n con el campo eléctrico, dos placas infinitas ($E_d$) y la posición en el eje z ($z$) se expresa como:
De manera similar, el campo eléctrico, dos placas infinitas ($E_d$) en relaci n con la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$) y la densidad de carga por área ($\sigma$) se define como:
Integrando desde el origen, obtenemos:
$\varphi_d = -\displaystyle\int_0^z du \displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon }= -\displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon } z$
Por lo tanto, el potencial eléctrico, dos placas infinitas ($\varphi_d$) resulta en:
Como se ilustra en la siguiente gr fica:
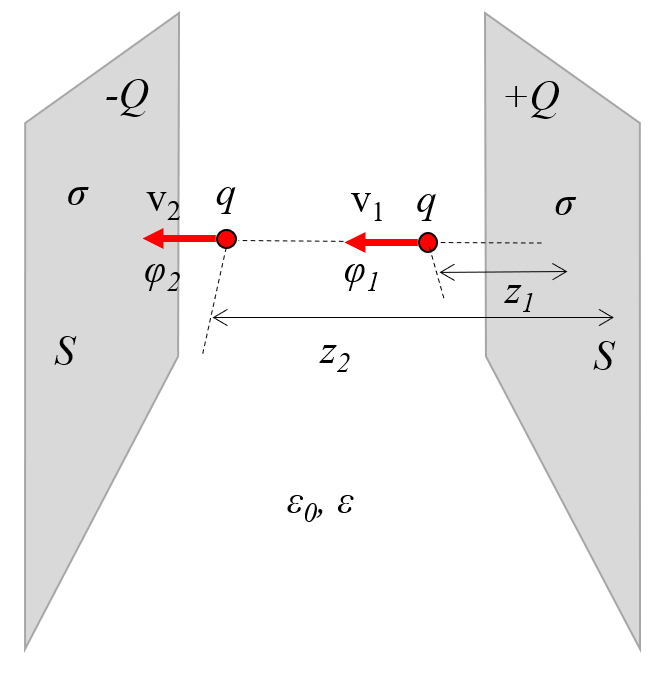
el campo en dos puntos debe poseer la misma energ a. Por lo tanto, las variables la carga ($Q$), la masa de la partícula ($m$), la velocidad 1 ($v_1$), la velocidad 2 ($v_2$), y el potencial eléctrico 1 ($\varphi_1$) seg n la ecuaci n:
y el potencial eléctrico 2 ($\varphi_2$), seg n la ecuaci n:
deben satisfacer la relaci n siguiente:
La densidad superficial de carga se calcula dividiendo la carga total por el rea de la superficie. Por lo tanto, la relaci n entre la densidad de carga por área ($\sigma$) y la carga ($Q$) con la área del conductor ($S$) se establece como:
El campo eléctrico, dos placas infinitas ($E_d$) es con la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$) y la densidad de carga por área ($\sigma$) es igual a:
El potencial eléctrico, dos placas infinitas ($\varphi_d$) es con la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$), la densidad de carga por área ($\sigma$) y la posición en el eje z ($z$) es igual a:
El potencial eléctrico, dos placas infinitas ($\varphi_d$) es con la constante de campo eléctrico ($\epsilon_0$), la constante dieléctrica ($\epsilon$), la densidad de carga por área ($\sigma$) y la posición en el eje z ($z$) es igual a:
Los potenciales el ctricos, que representan la energ a potencial por unidad de carga, influyen en c mo var a la velocidad de una part cula. Por consiguiente, la conservaci n de la energ a entre dos puntos implica que, en presencia de las variables la carga ($q$), la masa de la partícula ($m$), la velocidad 1 ($v_1$), la velocidad 2 ($v_2$), el potencial eléctrico 1 ($\varphi_1$) y el potencial eléctrico 2 ($\varphi_2$), se debe cumplir la siguiente relaci n:
ID:(2076, 0)