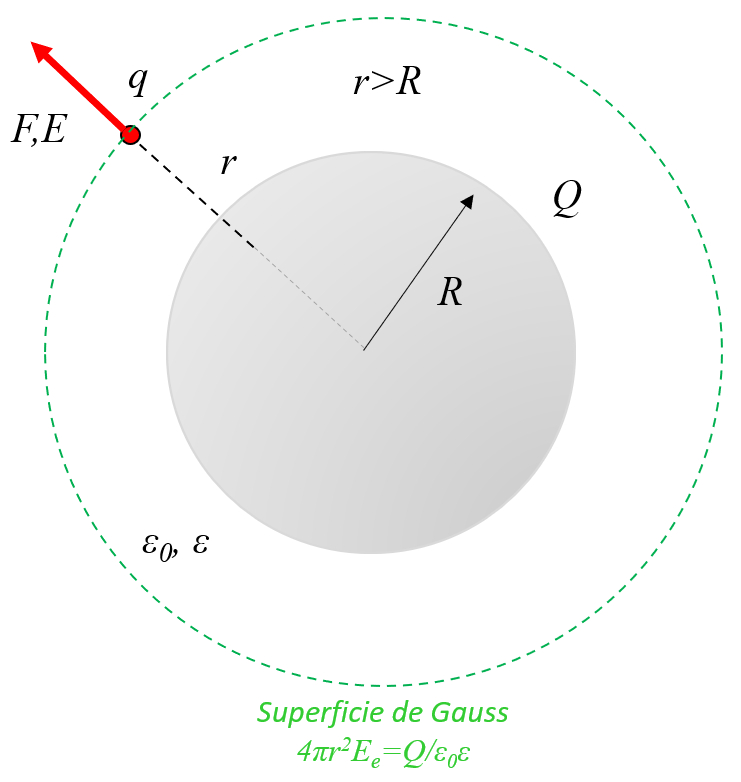
Exterior of a sphere
Storyboard 
For both a conducting sphere and an insulating sphere, the external field depends only on the total charge, whether it is distributed on the surface (conducting sphere) or throughout the interior (insulating sphere).
ID:(2078, 0)
Exterior of a sphere
Storyboard 
For both a conducting sphere and an insulating sphere, the external field depends only on the total charge, whether it is distributed on the surface (conducting sphere) or throughout the interior (insulating sphere).
Variables
Calculations
Calculations
Equations
In the case of a spherical Gaussian surface, the electric field is constant, so the electric eield ($E$) can be calculated using the charge ($Q$), the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$), and the surface of the conductor ($S$), resulting in:
Given that the surface of a sphere ($S$) is equal to the pi ($\pi$) and the disc radius ($r$), we obtain:
Finally, the electric field, sphere, outer ($E_e$) together with the distance between charges ($r$) is equal to:
Considering a spherical Gaussian surface, the electric field is constant. Therefore, the electric eield ($E$) is equal to the charge ($Q$), the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$), and the surface of the conductor ($S$) as shown by:
Since the surface area of the surface of a sphere ($S$) is equal to the pi ($\pi$) and the disc radius ($r$), we have:
The charge enclosed by the Gaussian surface, with the encapsulated charge on Gauss surface ($q$), the sphere radius ($R$), and the distance between charges ($r$), is given by:
Therefore, the electric field, sphere, interior ($E_i$) results in:
As the potential difference is the reference electrical, insulating sphere, inner ($\varphi_i$) with the electric field, sphere, interior ($E_i$) and the radius ($r$), we get:
Given that the electric field, sphere, interior ($E_i$) with the pi ($\pi$), the charge ($Q$), the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$), the sphere radius ($R$), and the distance between charges ($r$) is equal to:
In spherical coordinates, this is:
$\varphi_i = -\displaystyle\int_0^{r} du \displaystyle\frac{ Q u }{4 \pi \epsilon_0 \epsilon R ^3 }= -\displaystyle\frac{ Q }{ 8 \pi \epsilon_0 \epsilon }\displaystyle\frac{ r ^2 }{ R ^3 }$
Therefore, the reference electrical, insulating sphere, inner ($\varphi_i$) with the distance between charges ($r$) results in:
As the potential difference is the reference electrical, sphere, outer ($\varphi_e$) with the electric field, sphere, outer ($E_e$), the electric field, sphere, interior ($E_i$), the sphere radius ($R$), and the radius ($r$), we get:
Given that the electric field, sphere, outer ($E_e$) with the pi ($\pi$), the charge ($Q$), the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$), and the distance between charges ($r$) is equal to:
and that the electric field, sphere, interior ($E_i$) with the internal radius ($r_i$) is equal to:
In spherical coordinates, we have:
$\varphi_e = -\displaystyle\int_0^R du \displaystyle\frac{ Q u }{4 \pi \epsilon_0 \epsilon R ^3 } -\displaystyle\int_R^r du \displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon u ^2 }= -\displaystyle\frac{ 1 }{ 4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r }$
Therefore, the reference electrical, sphere, outer ($\varphi_e$) results in:
Examples
In the case of a spherical Gaussian surface, the electric field ($\vec{E}$) is constant in the direction of the versor normal to the section ($\hat{n}$). Therefore, using the charge ($Q$), the electric field constant ($\epsilon_0$), and the dielectric constant ($\epsilon$), it can be calculated by integrating over the surface where the electric field is constant ($dS$):
Since the surface area of the surface of a sphere ($S$) is equal to the pi ($\pi$) and the disc radius ($r$), we have:
what is shown in the graph
Outside the sphere, the electric field, sphere, outer ($E_e$) with the pi ($\pi$), the charge ($Q$), the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$), and the distance between charges ($r$) is equal to:
While in the case of an insulating sphere, the electric field, sphere, interior ($E_i$) with the sphere radius ($R$) is:
If the sphere is conductive, the charges will distribute over the surface, and the electric field, sphere, interior ($E_i$) will be zero.
As the potential difference is the reference electrical, sphere, outer ($\varphi_e$) with the electric field, sphere, outer ($E_e$), the electric field, sphere, interior ($E_i$), the sphere radius ($R$), and the radius ($r$), we get:
Given that the electric field, sphere, outer ($E_e$) with the pi ($\pi$), the charge ($Q$), the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$), and the distance between charges ($r$) is equal to:
and that the electric field, sphere, interior ($E_i$) with the internal radius ($r_i$) is equal to:
In spherical coordinates, we have:
$\varphi_e = -\displaystyle\int_0^R du \displaystyle\frac{ Q u }{4 \pi \epsilon_0 \epsilon R ^3 } -\displaystyle\int_R^r du \displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon u ^2 }= -\displaystyle\frac{ 1 }{ 4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r }$
Therefore, the reference electrical, sphere, outer ($\varphi_e$) results in:
As illustrated in the following graph:
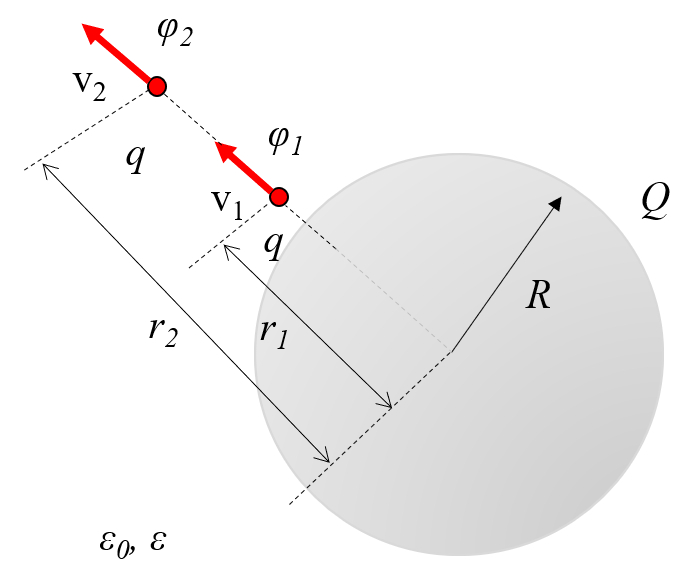
the field at two points must have the same energy. Therefore, the variables the charge ($Q$), the particle mass ($m$), the speed 1 ($v_1$), the speed 2 ($v_2$), and the electric potential 1 ($\varphi_1$) according to the equation:
and the electric potential 2 ($\varphi_2$), according to the equation:
must satisfy the following relationship:
The electric field, sphere, interior ($E_i$) is with the pi ($\pi$), the charge ($Q$), the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$), the sphere radius ($R$) and the distance between charges ($r$) is equal to:
The electric field, sphere, outer ($E_e$) is with the pi ($\pi$), the charge ($Q$), the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$) and the distance between charges ($r$) is equal to:
The reference electrical, insulating sphere, inner ($\varphi_i$) is with the pi ($\pi$), the charge ($Q$), the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$), the distance between charges ($r$) and the sphere radius ($R$) is equal to:
The reference electrical, sphere, outer ($\varphi_e$) is with the pi ($\pi$), the charge ($Q$), the electric field constant ($\epsilon_0$), the dielectric constant ($\epsilon$) and the distance between charges ($r$) is equal to:
Electric potentials, which represent potential energy per unit of charge, influence how the velocity of a particle varies. Consequently, due to the conservation of energy between two points, it follows that in the presence of variables the charge ($q$), the particle mass ($m$), the speed 1 ($v_1$), the speed 2 ($v_2$), the electric potential 1 ($\varphi_1$), and the electric potential 2 ($\varphi_2$), the following relationship must be satisfied:
ID:(2078, 0)