Utilizador:
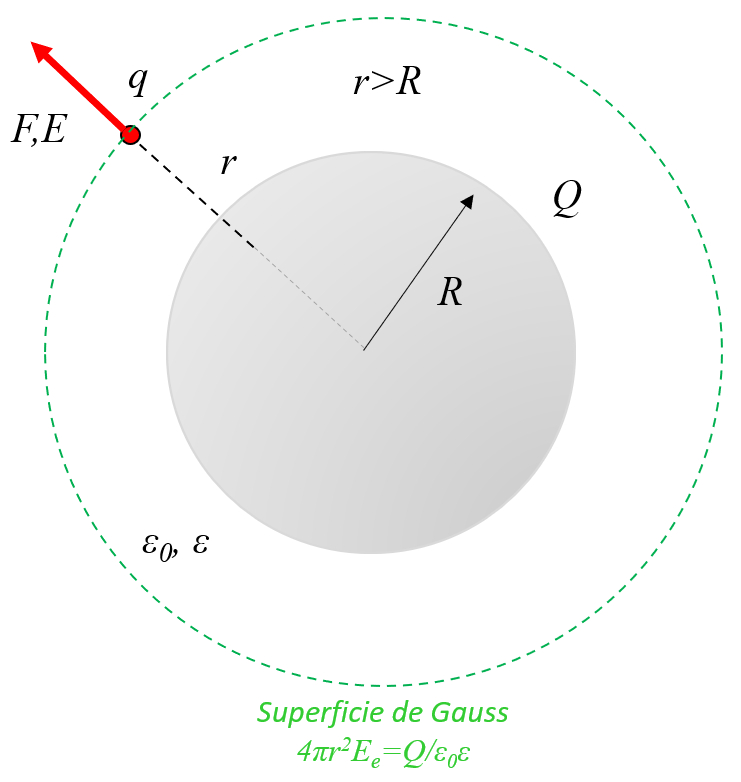
Exterior de uma esfera
Storyboard 
Tanto para uma esfera condutora quanto para uma esfera isolante, o campo externo depende apenas da carga total, seja ela distribuída na superfície (esfera condutora) ou no interior (esfera isolante).
ID:(2078, 0)
Partícula no campo elétrico de uma esfera externa
Conceito
No caso de uma superfície gaussiana esférica, o campo elétrico ($\vec{E}$) é constante na direção de o versor normal para seção ($\hat{n}$). Portanto, utilizando la charge ($Q$), la constante de campo elétrico ($\epsilon_0$) e la constante dielétrica ($\epsilon$), pode-se calcular integrando sobre la superfície na qual o campo elétrico é constante ($dS$):
| $\displaystyle\int_S\vec{E}\cdot\hat{n}\,dS=\displaystyle\frac{Q}{\epsilon_0\epsilon}$ |
Dado que a área da superfície de la superfície de uma esfera ($S$) é igual a o pi ($\pi$) e o raio do disco ($r$), temos:
| $ S = 4 \pi r ^2$ |
o que é mostrado no gráfico
Fora da esfera, o campo elétrico, esfera, exterior ($E_e$) com o pi ($\pi$), la charge ($Q$), la constante de campo elétrico ($\epsilon_0$), la constante dielétrica ($\epsilon$) e la distância entre cargas ($r$) é igual a:
| $ E_e=\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r_2 ^2 }$ |
Enquanto no caso de uma esfera isolante, o campo elétrico, esfera, interior ($E_i$) com o raio da esfera ($R$) é:
| $ E_i =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q r_1 }{ R ^3 }$ |
Se a esfera for condutora, as cargas se distribuirão sobre a superfície e o campo elétrico, esfera, interior ($E_i$) será zero.
ID:(11839, 0)
Partícula no potencial elétrico de uma esfera externa
Conceito
Como a diferença de potencial é O potencial elétrico, esfera, exterior ($\varphi_e$) com o campo elétrico, esfera, exterior ($E_e$), o campo elétrico, esfera, interior ($E_i$), o raio da esfera ($R$) e o rádio ($r$), obtemos:
| $ \varphi_e = - \displaystyle\int_0^ R du\, E_i - \displaystyle\int_ R ^ r du\, E_e $ |
Dado que o campo elétrico, esfera, exterior ($E_e$) com o pi ($\pi$), la charge ($Q$), la constante de campo elétrico ($\epsilon_0$), la constante dielétrica ($\epsilon$) e la distância entre cargas ($r$) é igual a:
| $ E_e=\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r_2 ^2 }$ |
e que o campo elétrico, esfera, interior ($E_i$) com ($$) é igual a:
| $ E_i =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q r_1 }{ R ^3 }$ |
em coordenadas esféricas, temos:
$\varphi_e = -\displaystyle\int_0^R du \displaystyle\frac{ Q u }{4 \pi \epsilon_0 \epsilon R ^3 } -\displaystyle\int_R^r du \displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon u ^2 }= -\displaystyle\frac{ 1 }{ 4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r }$
Portanto, o potencial elétrico, esfera, exterior ($\varphi_e$) resulta em:
| $ \varphi_2 = -\displaystyle\frac{ 1 }{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r_2 } $ |
Como ilustrado no seguinte gráfico:
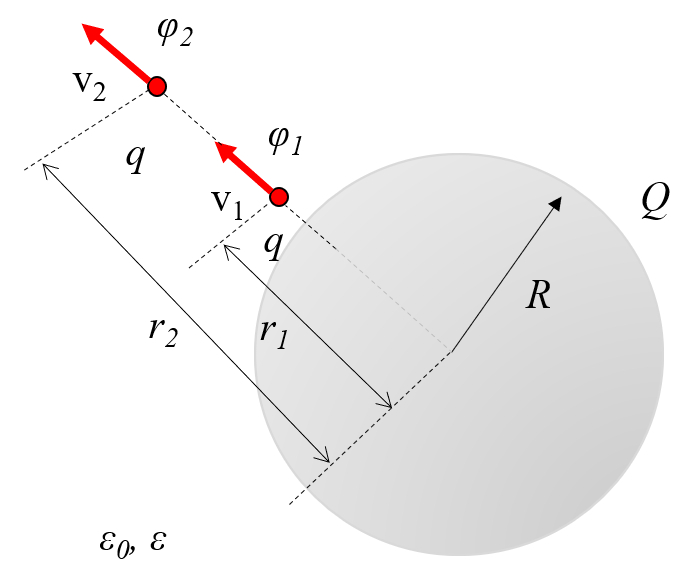
o campo em dois pontos deve possuir a mesma energia. Portanto, as variáveis la charge ($Q$), la massa molar ($m$), la velocidade 1 ($v_1$), la velocidade 2 ($v_2$) e o potencial elétrico 1 ($\varphi_1$) conforme a equação:
e o potencial elétrico 2 ($\varphi_2$), conforme a equação:
devem satisfazer a seguinte relação:
| $ \displaystyle\frac{1}{2} m v_1 ^2 + q \varphi_1 = \displaystyle\frac{1}{2} m v_2 ^2 + q \varphi_2 $ |
ID:(11846, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ E_e=\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r_2 ^2 }$
E_e = Q /(4 * pi * epsilon_0 * epsilon * r ^2)
$ E_i =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q r_1 }{ R ^3 }$
E_i = Q * r /(4 * pi * epsilon_0 * epsilon * R ^3)
$ \displaystyle\frac{1}{2} m v_1 ^2 + q \varphi_1 = \displaystyle\frac{1}{2} m v_2 ^2 + q \varphi_2 $
m * v_1 ^2/2 + q * phi_1 = m * v_2 ^2/2 + q * phi_2
$ \varphi_2 = -\displaystyle\frac{ 1 }{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r_2 } $
phi_e =- Q / (4 * pi * epsilon * epsilon_0 * r )
$ \varphi_1 = -\displaystyle\frac{ Q }{8 \pi \epsilon_0 \epsilon }\displaystyle\frac{ r_1 ^2 }{ R ^3 }$
phi_i =- Q * r ^2/(8 * pi * epsilon * epsilon_0 * R ^3)
ID:(15807, 0)
Esfera isolante com carga em todo o volume, interior
Equação
O campo elétrico, esfera, interior ($E_i$) é com o pi ($\pi$), la charge ($Q$), la constante de campo elétrico ($\epsilon_0$), la constante dielétrica ($\epsilon$), o raio da esfera ($R$) e la distância entre cargas ($r$) é igual a:
| $ E_i =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q r_1 }{ R ^3 }$ |
| $ E_i =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q r }{ R ^3 }$ |
Para o caso de uma superfície gaussiana esférica, o campo elétrico é constante. Portanto, o campo elétrico ($E$) é igual a la charge ($Q$), la constante de campo elétrico ($\epsilon_0$), la constante dielétrica ($\epsilon$) e la zona do condutor ($S$) conforme:
| $ E S = \displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$ |
Dado que a área da superfície de la superfície de uma esfera ($S$) é igual a o pi ($\pi$) e o raio do disco ($r$), temos:
| $ S = 4 \pi r ^2$ |
A carga encerrada na superfície gaussiana, com la carga encapsulada na superfície gaussiana ($q$), o raio da esfera ($R$) e la distância entre cargas ($r$), é dada por:
| $ q =\displaystyle\frac{ r ^3}{ R ^3} Q $ |
Portanto, o campo elétrico, esfera, interior ($E_i$) resulta em:
| $ E_i =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q r }{ R ^3 }$ |
ID:(11447, 0)
Esfera isolante com carga em todo o volume, exterior
Equação
O campo elétrico, esfera, exterior ($E_e$) é com o pi ($\pi$), la charge ($Q$), la constante de campo elétrico ($\epsilon_0$), la constante dielétrica ($\epsilon$) e la distância entre cargas ($r$) é igual a:
| $ E_e=\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r_2 ^2 }$ |
| $ E_e=\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r ^2 }$ |
No caso de uma superfície gaussiana esférica, o campo elétrico é constante, de modo que o campo elétrico ($E$) pode ser calculado usando la charge ($Q$), la constante de campo elétrico ($\epsilon_0$), la constante dielétrica ($\epsilon$) e la zona do condutor ($S$), resultando em:
| $ E S = \displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$ |
Dado que la superfície de uma esfera ($S$) é igual a o pi ($\pi$) e o raio do disco ($r$), obtemos:
| $ S = 4 \pi r ^2$ |
Finalmente, o campo elétrico, esfera, exterior ($E_e$) junto com la distância entre cargas ($r$) é igual a:
| $ E_e=\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r ^2 }$ |
ID:(11446, 0)
Cálculo do potencial elétrico com geometria interna esférica
Equação
O potencial elétrico, esfera isolante, interior ($\varphi_i$) é com o pi ($\pi$), la charge ($Q$), la constante de campo elétrico ($\epsilon_0$), la constante dielétrica ($\epsilon$), la distância entre cargas ($r$) e o raio da esfera ($R$) é igual a:
| $ \varphi_1 = -\displaystyle\frac{ Q }{8 \pi \epsilon_0 \epsilon }\displaystyle\frac{ r_1 ^2 }{ R ^3 }$ |
| $ \varphi_i = -\displaystyle\frac{ Q }{8 \pi \epsilon_0 \epsilon }\displaystyle\frac{ r ^2 }{ R ^3 }$ |
Como a diferença de potencial é O potencial elétrico, esfera isolante, interior ($\varphi_i$) com o campo elétrico, esfera, interior ($E_i$) e o rádio ($r$), obtemos:
| $ \varphi_i = -\displaystyle\int_0^ r du\, E_i $ |
Dado que o campo elétrico, esfera, interior ($E_i$) com o pi ($\pi$), la charge ($Q$), la constante de campo elétrico ($\epsilon_0$), la constante dielétrica ($\epsilon$), o raio da esfera ($R$) e la distância entre cargas ($r$) é igual a:
| $ E_i =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q r_1 }{ R ^3 }$ |
Em coordenadas esféricas, temos:
$\varphi_i = -\displaystyle\int_0^{r} du \displaystyle\frac{ Q u }{4 \pi \epsilon_0 \epsilon R ^3 }= -\displaystyle\frac{ Q }{ 8 \pi \epsilon_0 \epsilon }\displaystyle\frac{ r ^2 }{ R ^3 }$
Portanto, o potencial elétrico, esfera isolante, interior ($\varphi_i$) com la distância entre cargas ($r$) resulta em:
| $ \varphi_i = -\displaystyle\frac{ Q }{8 \pi \epsilon_0 \epsilon }\displaystyle\frac{ r ^2 }{ R ^3 }$ |
ID:(11583, 0)
Cálculo de potencial elétrico com geometria esférica, externo
Equação
O potencial elétrico, esfera, exterior ($\varphi_e$) é com o pi ($\pi$), la charge ($Q$), la constante de campo elétrico ($\epsilon_0$), la constante dielétrica ($\epsilon$) e la distância entre cargas ($r$) é igual a:
| $ \varphi_2 = -\displaystyle\frac{ 1 }{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r_2 } $ |
| $ \varphi_e = -\displaystyle\frac{ 1 }{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r } $ |
Como a diferença de potencial é O potencial elétrico, esfera, exterior ($\varphi_e$) com o campo elétrico, esfera, exterior ($E_e$), o campo elétrico, esfera, interior ($E_i$), o raio da esfera ($R$) e o rádio ($r$), obtemos:
| $ \varphi_e = - \displaystyle\int_0^ R du\, E_i - \displaystyle\int_ R ^ r du\, E_e $ |
Dado que o campo elétrico, esfera, exterior ($E_e$) com o pi ($\pi$), la charge ($Q$), la constante de campo elétrico ($\epsilon_0$), la constante dielétrica ($\epsilon$) e la distância entre cargas ($r$) é igual a:
| $ E_e=\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r_2 ^2 }$ |
e que o campo elétrico, esfera, interior ($E_i$) com ($$) é igual a:
| $ E_i =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q r_1 }{ R ^3 }$ |
em coordenadas esféricas, temos:
$\varphi_e = -\displaystyle\int_0^R du \displaystyle\frac{ Q u }{4 \pi \epsilon_0 \epsilon R ^3 } -\displaystyle\int_R^r du \displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon u ^2 }= -\displaystyle\frac{ 1 }{ 4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r }$
Portanto, o potencial elétrico, esfera, exterior ($\varphi_e$) resulta em:
| $ \varphi_e = -\displaystyle\frac{ 1 }{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r } $ |
ID:(11584, 0)
Energia de uma partícula
Equação
Os potenciais elétricos, que representam a energia potencial por unidade de carga, influenciam como a velocidade de uma partícula varia. Consequentemente, devido à conservação de energia entre dois pontos, segue-se que na presença das variáveis la carga ($q$), la massa molar ($m$), la velocidade 1 ($v_1$), la velocidade 2 ($v_2$), o potencial elétrico 1 ($\varphi_1$) e o potencial elétrico 2 ($\varphi_2$), a seguinte relação deve ser satisfeita:
| $ \displaystyle\frac{1}{2} m v_1 ^2 + q \varphi_1 = \displaystyle\frac{1}{2} m v_2 ^2 + q \varphi_2 $ |
ID:(11596, 0)