Examples of electrical potentials
Storyboard
With the examples of the electric fields calculated above, the electric potentials are calculated.
ID:(1562, 0)
Energy of a particle
Equation
Los potenciales eléctricos corresponden a energía potencial por carga por lo que generan o reducen velocidad en función de como aumenta o reduce la energía potencial. Por ello la conservación de energía lleva a que con
| $ \displaystyle\frac{1}{2} m v_1 ^2 + q \varphi_1 = \displaystyle\frac{1}{2} m v_2 ^2 + q \varphi_2 $ |
ID:(11596, 0)
Conductor sphere with charge
Image
In a conducting sphere with charges, these are distributed on the surface and with it the field inside is null. Outside it behaves like a point charge that is in the center of the sphere:
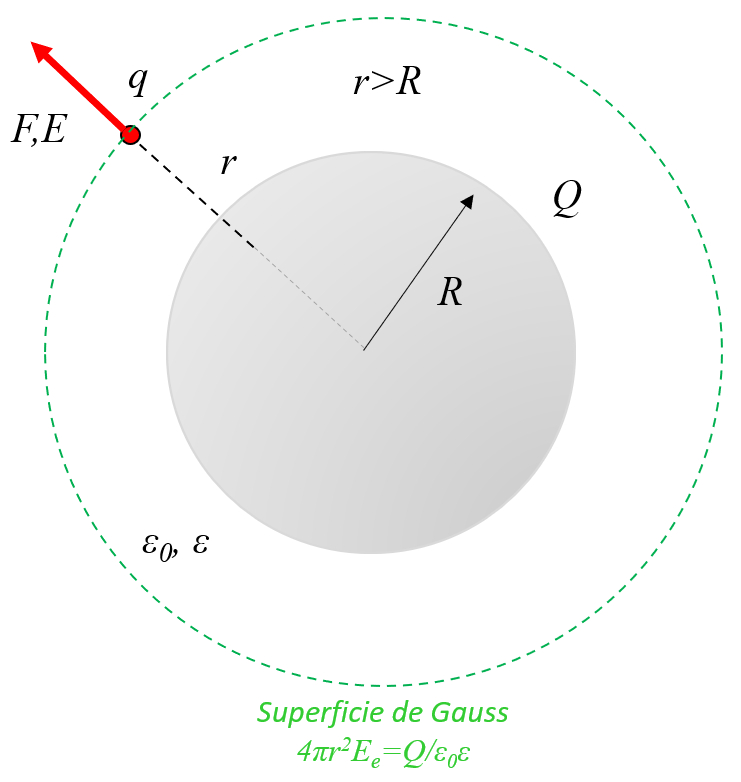
ID:(11451, 0)
Calculation of electrical potentials, point charge
Equation
Como la diferencia de potencial es con igual
| $ \varphi_p = -\displaystyle\int_r^{\infty} du\,E_p(u)$ |
con
| $ E_p =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{Q}{ r ^2}$ |
\\n\\nlo que en coordenadas esféricas es\\n\\n
$\varphi_p = -\displaystyle\int_{r}^{\infty} du \displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon u ^2 }= -\displaystyle\frac{ Q }{ 4 \pi \epsilon_0 \epsilon }\displaystyle\frac{1}{ r }$
o sea con
| $ \varphi_p = -\displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{1}{ r } $ |
ID:(11576, 0)
Calculation of electrical potentials, with spherical geometry, external
Equation
Como la diferencia de potencial con es igual
| $ \varphi_f = -\displaystyle\int_r^{\infty} du\,E_f(u)$ |
con
| $ E_f =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{Q}{ r ^2}\theta( r - R )$ |
\\n\\nlo que en coordenadas esféricas es\\n\\n
$\varphi_f = -\displaystyle\int_{\infty}^{r} du \displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon u ^2 }= -\displaystyle\frac{ Q }{ 4 \pi \epsilon_0 \epsilon }\displaystyle\frac{1}{ r }$
o sea con
| $ \varphi_f = -\displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{1}{ r } $ |
ID:(11582, 0)
Insulating sphere with homogeneous charge
Image
An insulating sphere in which charges have been homogeneously distributed, which cannot be moved because it is an insulating material, has an electric field that grows linearly inside and decreases with the inverse of the radius squared:
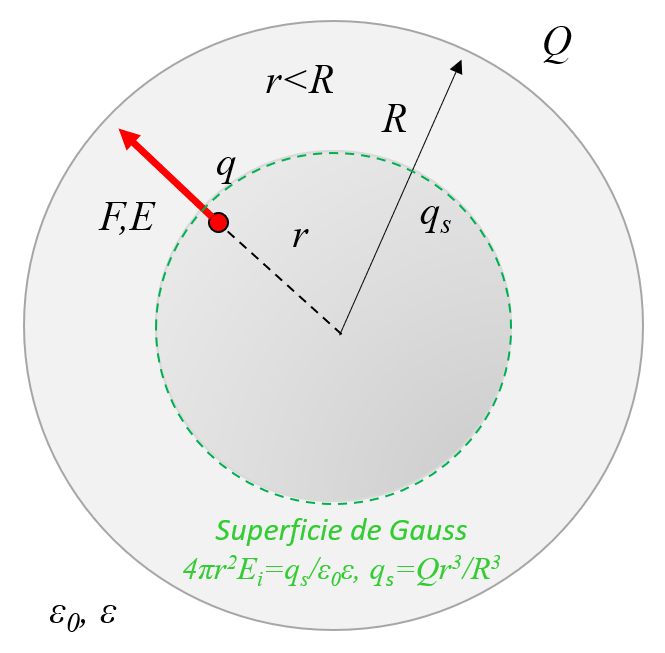
ID:(11450, 0)
Calculation of electric potential with spherical geometry, insulator, internal
Equation
Como la diferencia de potencial es con igual
| $ \varphi_i = -\displaystyle\int_0^r du\,E_i(u)$ |
con
| $ E_i =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q r_i }{ R ^3 }$ |
\\n\\nlo que en coordenadas esféricas es\\n\\n
$\varphi_i = -\displaystyle\int_0^{r} du \displaystyle\frac{ Q u }{4 \pi \epsilon_0 \epsilon R ^3 }= -\displaystyle\frac{ Q }{ 8 \pi \epsilon_0 \epsilon }\displaystyle\frac{ r ^2 }{ R ^3 }$
o sea con
| $ \varphi_i = -\displaystyle\frac{ Q }{8 \pi \epsilon_0 \epsilon }\displaystyle\frac{ r ^2 }{ R ^3 }\theta( R - r ) $ |
ID:(11583, 0)
Calculation of electric potential with spherical geometry, insulator, external
Equation
Como la diferencia de potencial es con igual
| $ \varphi_e = - \displaystyle\int_0^R du\,E_i(u) - \displaystyle\int_R^r du\,E_e(u)$ |
con
| $ E_e=\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r ^2 }$ |
y con
| $ E_i =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q r_i }{ R ^3 }$ |
\\n\\nlo que en coordenadas esféricas es\\n\\n
$\varphi_e = -\displaystyle\int_0^R du \displaystyle\frac{ Q u }{4 \pi \epsilon_0 \epsilon R ^3 } -\displaystyle\int_R^r du \displaystyle\frac{ Q }{4 \pi \epsilon_0 \epsilon u ^2 }= -\displaystyle\frac{ 1 }{ 4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r }$
o sea con
| $ \varphi_e = -\displaystyle\frac{ 1 }{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r } $ |
ID:(11584, 0)
Loaded infinite wire or cylinder, in vacuum
Image
In a conductor wire or cylinder with charges, these are distributed throughout the object, behaving like a long chain of point loads aligned on the axis:
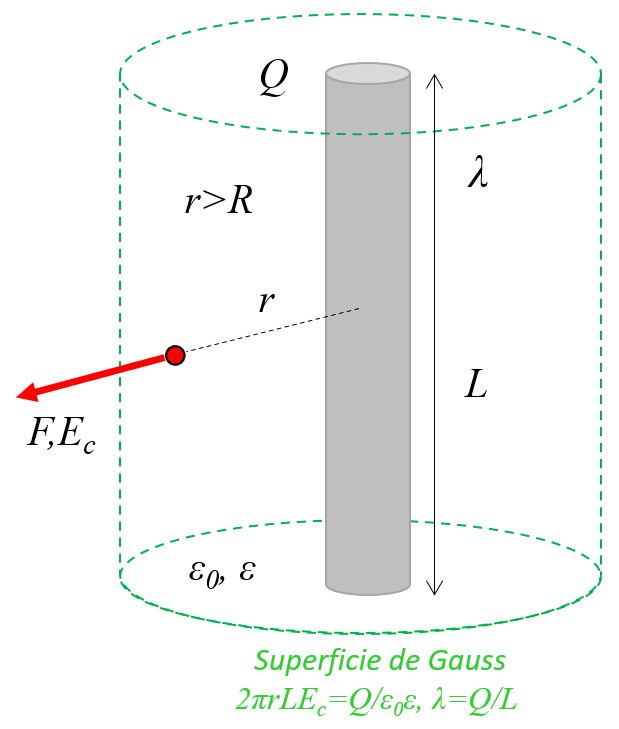
ID:(11452, 0)
Calculation of electrical potentials, cylindrical geometry
Equation
Como la diferencia de potencial es con igual
| $ \varphi_c = -\displaystyle\int_{r_0}^r du\,E_c(u)$ |
con
| $ E_c =\displaystyle\frac{1}{2 \pi \epsilon_0 \epsilon }\displaystyle\frac{ \lambda }{ r }\theta( r - R )$ |
\\n\\nlo que en coordenadas esféricas es\\n\\n
$\varphi_c = -\displaystyle\int_{r_0}^r du \displaystyle\frac{ \lambda }{ 2 \pi \epsilon_0 \epsilon u }= -\displaystyle\frac{ \lambda }{ 2 \pi \epsilon_0 \epsilon } \ln r$
o sea con
| $ \varphi_c = -\displaystyle\frac{ \lambda }{ 2 \pi \epsilon_0 \epsilon }\ln r $ |
ID:(11585, 0)
Infinite conductor plane with load
Image
In a conducting plane, a Gaussian surface can be defined as a cylinder. The side walls are orthogonal to the field, so the only part that contributes are the surfaces parallel to the plane:
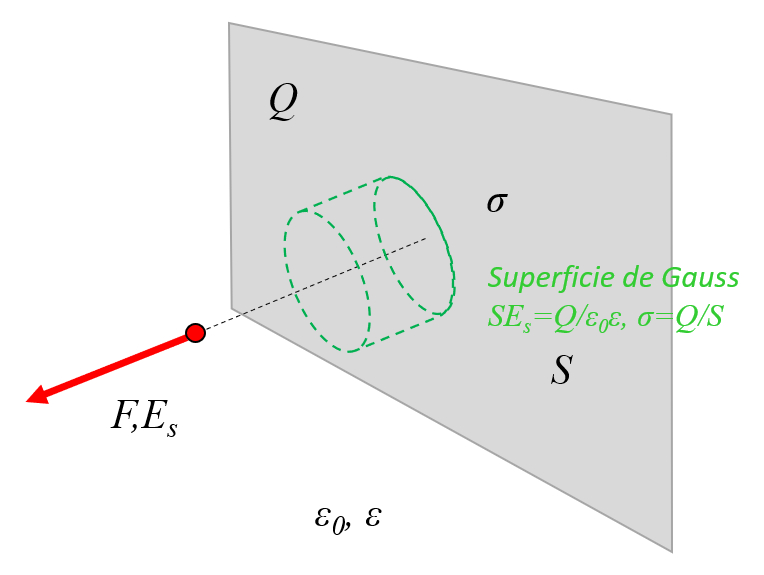
ID:(11453, 0)
Calculation of electrical potential, surfaces
Equation
Como la diferencia de potencial es con igual
| $ \varphi_{s,d} = -\displaystyle\int_0^z du\,E_{s,d}(u)$ |
con
| $ E_s =\displaystyle\frac{ \sigma }{ 2 \epsilon_0 \epsilon }$ |
\\n\\nlo que en coordenadas esféricas es\\n\\n
$\varphi_s = -\displaystyle\int_0^z du \displaystyle\frac{ \sigma }{2 \epsilon_0 \epsilon }= -\displaystyle\frac{ \sigma }{2 \epsilon_0 \epsilon } z$
o sea con
| $ \varphi_s = -\displaystyle\frac{ \sigma }{2 \epsilon_0 \epsilon } z $ |
ID:(11586, 0)
Simple model for two plates with opposite charges
Image
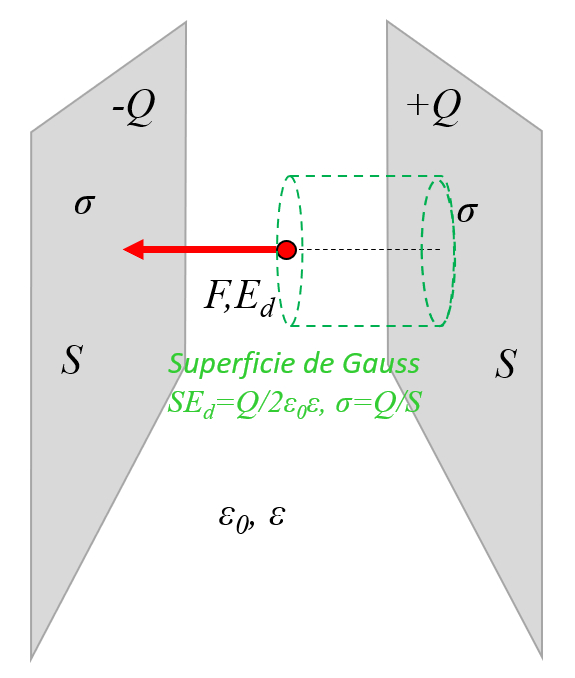
To be able to calculate the field between the two plates in a simple way, it can be assumed that the external field is compensated and that most of it is only between the plates:
ID:(11455, 0)
Calculation of electrical potentials, double plate
Equation
Como la diferencia de potencial es con igual
| $ \varphi_{s,d} = -\displaystyle\int_0^z du\,E_{s,d}(u)$ |
con
| $ E_d =\displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon }$ |
\\n\\nlo que en coordenadas esféricas es\\n\\n
$\varphi_d = -\displaystyle\int_0^z du \displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon }= -\displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon } z$
o sea con
| $ \varphi_d = -\displaystyle\frac{ \sigma }{ \epsilon_0 \epsilon } z $ |
ID:(11587, 0)
0
Video
Video: Examples of electrical potentials
