User:
Working converter heat
Description
The conversion of work into energy is studied by generating heat through friction. To do this, a metal band is wrapped around a cylinder containing water and a thermometer. By turning the crank, heat is generated through friction, leading to the heating of the water. If the applied force, the number of rotations, and the radius of the cylinder are measured, the distance traveled can be estimated, allowing for the estimation of energy as the product of force and distance.
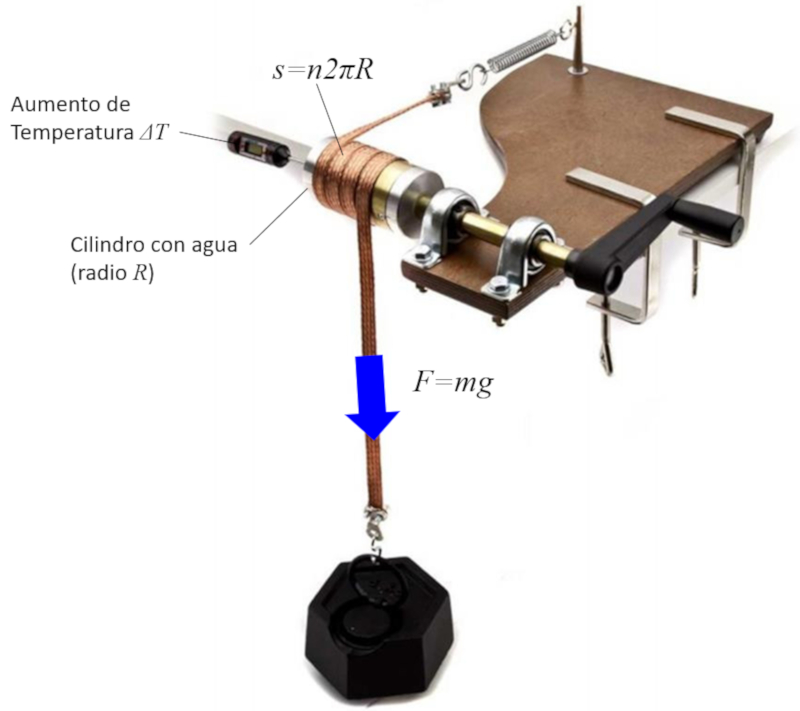
ID:(1884, 0)
Definition of energy
Equation
The concept of energy was initially introduced in thermodynamics to quantify the amount of heat that could be converted into mechanical work. In a specific experiment, a surface was rubbed against a tensioned cable with a force. The cable effectively covered a distance that, when multiplied by the applied force, yielded the amount of energy.
$\Delta W = F \Delta s$
Since both the force and the distance are actually vectors, this expression can be generalized using the dot product of the force with the distance:
 $ \Delta W = \vec{F} \cdot \Delta\vec{s} $ |
In other words, only the component of the force that truly displaces the object contributes to its energy.
ID:(1136, 0)
Path definition
Image
For any given path, it's possible to define the force acting at each point. Furthermore, if we break down this path into distinct segments represented by vectors $d\vec{x}$, we can calculate the dot product between them to determine the energy being consumed:
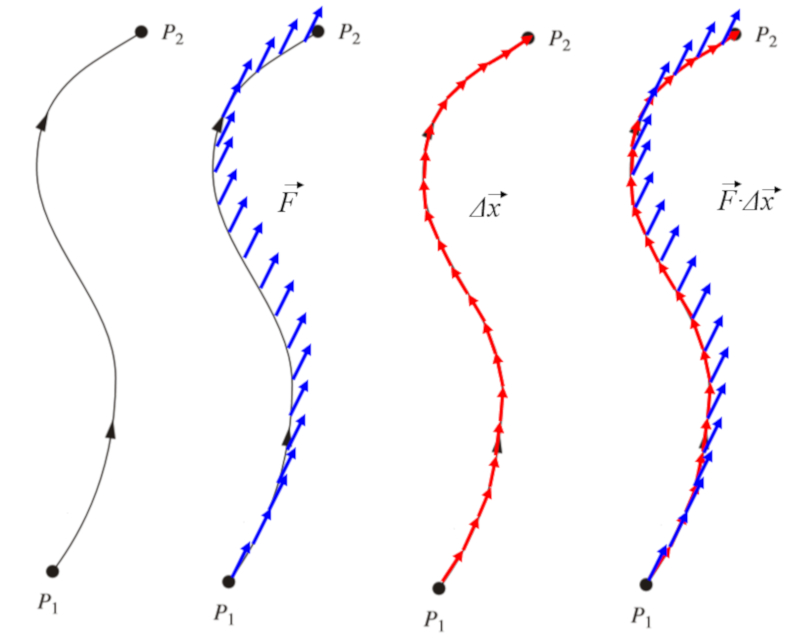
ID:(11514, 0)
General definition of energy
Equation
Carnot was the first to describe energy in terms of the path and the necessary force to traverse it. Progressing along a path with a force requires or generates energy. This corresponds to the equation:
| $ \Delta W = \vec{F} \cdot \Delta\vec{s} $ |
In the continuous limit, the sum can be represented as an integral:
| $ W =\displaystyle\int_C \vec{F} \cdot d \vec{s} $ |
Expanding the concept to a longer path involves summing up the energy required for each path element:
$\bar{W}=\displaystyle\sum_i \vec{F}_i\cdot\Delta\vec{s}_i$
However, the value of this equation represents just an average energy required or generated. The precise energy is obtained when the steps become very small, allowing the force to be considered constant within them:
$W=\displaystyle\sum_i \mbox{lim}_{\Delta\vec{s}_i\rightarrow\vec{0}}\vec{F}_i\cdot\Delta\vec{s}_i$
In this limit, the energy corresponds to the integral along the traveled path, giving us:
| $ W =\displaystyle\int_C \vec{F} \cdot d \vec{s} $ |
ID:(3601, 0)
Energy as a function of torque
Equation
Similar to how energy as a function of force and distance traveled is given by
| $ \Delta W = \vec{F} \cdot \Delta\vec{s} $ |
analogously, for rotation, the energy as a function of torque is expressed as
| $ \Delta W = T \Delta\theta $ |
Using the traditional definition of energy as
| $ \Delta W = \vec{F} \cdot \Delta\vec{s} $ |
in the case of rotation, the force is perpendicular to the radius, tangential to the orbit, and parallel to the arc, which is expressed as
| $ \Delta s=r \Delta\theta $ |
so with
| $ T = r F $ |
we find that
$\Delta W = \vec{F}\cdot\Delta\vec{s}=F\Delta s = F r\Delta\theta = T\Delta\theta$
meaning
| $ \Delta W = T \Delta\theta $ |
ID:(12550, 0)
General definition of rotation case energy
Equation
Carnot was the pioneer in describing energy based on the path and the necessary force to traverse it. Advancing along a path with a force requires or generates energy. This corresponds to the equation:
| $ \Delta W = T \Delta\theta $ |
In the continuous limit, the sum can be represented as an integral:
| $ W =\displaystyle\int_C T d \theta $ |
Expanding the concept to a longer path involves summing up the energy required for each path element:
$\bar{W}=\displaystyle\sum_i T_i\Delta\theta_i$
However, the value of this equation represents just an average energy required or generated. The precise energy is obtained when the steps become very small, allowing the torque to be considered constant within them:
$W=\displaystyle\sum_i \mbox{lim}_{\Delta\theta_i\rightarrow 0} T_i\Delta\theta_i$
In this limit, the energy corresponds to the integral along the traveled path, giving us:
| $ W =\displaystyle\int_C T d \theta $ |
ID:(321, 0)
0
Video
Video: Energy