Utilisateur:
Le décollage
Storyboard
La clé pour décoller est de modifier l'aile de manière à obtenir une portance suffisante à des vitesses plus basses, ce qui permet un décollage réussi sur une longueur de piste donnée.
ID:(1464, 0)
Coefficient de portance
Description
Le coefficient de portance est une fonction de l'angle d\'attaque et suit généralement la tendance indiquée dans la figure suivante :
Dans le cas illustré, la pente est d\'environ 1,5 pour 15 degrés, ce qui correspond à 0,1 1/degré ou 5,73 1/radian.
ID:(7148, 0)
Variation du coefficient de portance
Description
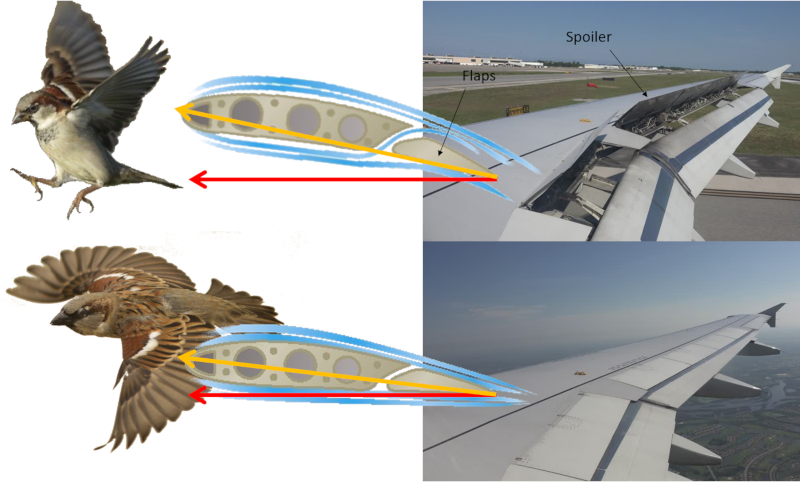
Les avions et les oiseaux sont capables de modifier la forme de leurs ailes. Les avions utilisent des volets (flaps), tandis que les oiseaux ajustent la position de leurs plumes primaires et secondaires. Ainsi, ils parviennent à obtenir un coefficient de portance élevé à basse vitesse lors du décollage et de l\'atterrissage, et un coefficient de portance réduit à haute vitesse.
De plus, les avions sont également équipés de spoilers qui aident à freiner lors de l\'atterrissage.
ID:(11072, 0)
Conditions de vol
Équation
Pour qu'un vaisseau spatial ou un oiseau puisse rester en vol, a force gravitationnelle ($F_g$) doit contrer la force de la gravité, définie par a masse corporelle ($m$) et a accélération gravitationnelle ($g$). En d'autres termes, il doit être :
 $ F_g = m g $ |
Il s'agit d'une situation simplifiée qui ne tient pas compte du fait que la force de résistance peut également générer une force de portance.
ID:(14515, 0)
Soulevez
Équation
Pour générer une pression plus élevée en dessous qu'au-dessus de l'aile et produire de la portance, le principe de Bernoulli est utilisé pour corriger le manque de conservation de la densité d'énergie avec un coefficient de portance ($C_L$). La pression sur l'aile, a force de levage ($F_L$), peut être estimée en utilisant a densité ($\rho$), a surface génératrice de portance ($S_w$), le coefficient de portance ($C_L$), et a vitesse par rapport au milieu ($v$) grâce à la formule suivante :
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
A force de levage ($F_L$), en compagnie de a envergure des ailes ($L$), a densité ($\rho$), le facteur de vitesse maximale de l'aile ($c_t$), le facteur de vitesse en bas d'aile ($c_b$), a longueur de l'aile supérieure ($l_t$), a longueur de l'aile inférieure ($l_b$) et a vitesse par rapport au milieu ($v$), se trouve dans
| $ F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$ |
Si nous considérons a surface génératrice de portance ($S_w$), défini par a envergure des ailes ($L$), a longueur de l'aile supérieure ($l_t$) et a longueur de l'aile inférieure ($l_b$),
| $ S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$ |
et pour le coefficient de portance ($C_L$), défini comme
| $ C_L = 4\displaystyle\frac{ c_t l_t - c_b l_b }{ l_t + l_b }$ |
nous obtenons
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
ID:(4417, 0)
Coefficient d'équilibre de portance
Équation
La condition pour atteindre le vol est remplie lorsque a force de levage ($F_L$) est égal au poids de l'aéronef ou de l'oiseau, calculé à partir de a masse corporelle ($m$) et a accélération gravitationnelle ($g$). Cela est réalisé avec des valeurs suffisantes de vitesse par rapport au milieu ($v$), a surface génératrice de portance ($S_w$), et le coefficient de portance ($C_L$), ce dernier coefficient étant le facteur ajustable. Dans le cas des aéronefs, les pilotes peuvent modifier la valeur de le coefficient de portance ($C_L$) en utilisant les volets, dont la valeur doit satisfaire à :
| $ C_L =\displaystyle\frac{2 m g }{ \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
A force de levage ($F_L$) avec a densité ($\rho$), a surface génératrice de portance ($S_w$), le coefficient de portance ($C_L$) et a vitesse par rapport au milieu ($v$) est représenté par
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
ce qui, avec a masse corporelle ($m$) et a accélération gravitationnelle ($g$), doit être égal à :
| $ F_g = m g $ |
c'est-à-dire :
$\displaystyle\frac{1}{2}\rho S_wC_Lv^2=mg$
ce qui donne :
| $ C_L =\displaystyle\frac{2 m g }{ \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
Les volets sont ajustés en modifiant l'angle que l'aile forme avec la direction du vol, connu sous le nom d'angle d'attaque.
ID:(4442, 0)
Constante de levage
Équation
À partir de mesures, il est conclu que le coefficient de portance $C_L$ est proportionnel à l'angle d\'attaque $\alpha$:
| $ C_L = c \alpha $ |
Après un certain angle, la courbe diminue jusqu\'à atteindre zéro. Cela est dû au fait que au-delà de cet angle critique, les tourbillons recouvrent entièrement la surface supérieure de l\'aile, ce qui entraîne une perte de portance. Ce phénomène est appelé \"décrochage\" ou \"décrochage aérodynamique\".
ID:(4441, 0)
Angle d'attaque
Équation
Étant donné que le coefficient de portance $C_L$ est proportionnel à l'angle d'attaque $\alpha$, on peut calculer l'angle nécessaire pour obtenir une portance suffisante pour une vitesse $v$ donnée :
| $ \alpha =\displaystyle\frac{2 m g }{ c \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
Le coefficient de portance ($C_L$) est calculé avec a masse corporelle ($m$), a accélération gravitationnelle ($g$), a surface génératrice de portance ($S_w$), a densité ($\rho$) et a vitesse par rapport au milieu ($v$) comme suit :
| $ C_L =\displaystyle\frac{2 m g }{ \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
Ainsi, avec a constante de proportionnalité du coefficient de portance ($c$) et le accélération maximale ($\alpha$),
| $ C_L = c \alpha $ |
nous obtenons
| $ \alpha =\displaystyle\frac{2 m g }{ c \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
où $m$ est la masse, $g$ est l\'accélération due à la gravité, $\rho$ est la densité du milieu, $S_w$ est la surface de l\'aile et $c$ est la constante de proportionnalité entre le coefficient de portance et l\'angle d\'attaque.
ID:(4443, 0)
Vitesse $V2$
Équation
Le décollage survient lorsque a vitesse par rapport au milieu ($v$) atteint un seuil suffisant pour que le accélération maximale ($\alpha$), sous l'influence des volets et de la rotation de l'avion, satisfasse à la condition suivante :
| $ \alpha =\displaystyle\frac{2 m g }{ c \rho S_w }\displaystyle\frac{1}{ v ^2}$ |
en tenant compte de a masse corporelle ($m$), a densité ($\rho$), a accélération gravitationnelle ($g$), le profil total de l'objet ($S_p$) et a constante de proportionnalité du coefficient de portance ($c$).
Dans cette situation, le accélération maximale ($\alpha$) est égal à Le angle nécessaire pour le levage ($\alpha_s$) et a vitesse par rapport au milieu ($v$) est égal à A vitesse critique $V2$ ($V2$) :
| $ V2 = \sqrt{\displaystyle\frac{2 m g }{ c \rho S_w \alpha_s }}$ |
ID:(14477, 0)
Vitesse de rotation $Vr$
Équation
A vitesse de rotation $Vr$ ($Vr$) est atteint lorsque l'avion peut décoller en ajustant l'angle de montée nécessaire. En d'autres termes, il correspond au scénario de a vitesse critique $V2$ ($V2$) avec a masse corporelle ($m$), a accélération gravitationnelle ($g$), a constante de proportionnalité du coefficient de portance ($c$), a accélération gravitationnelle ($g$), le profil total de l'objet ($S_p$) et le angle nécessaire pour le levage ($\alpha_s$) :
| $ V2 = \sqrt{\displaystyle\frac{2 m g }{ c \rho S_w \alpha_s }}$ |
lorsque l'avion n'a pas encore pivoté, et le angle nécessaire pour le levage ($\alpha_s$) est égal à Le accélération maximale ($\alpha$), qui ne tient pas compte de la rotation de l'avion. En résumé :
| $ Vr = \sqrt{\displaystyle\frac{2 m g }{ c \rho S_w \alpha }}$ |
ID:(14474, 0)
Accélération au décollage
Équation
Essentiellement, les aéronefs utilisent des systèmes de propulsion pour atteindre l'accélération nécessaire. Cette a force de propulsion ($F_p$) est contrée par a force de résistance ($F_W$), qui, avec a densité ($\rho$), le profil total de l'objet ($S_p$), le coefficient de résistance ($C_W$) et a vitesse par rapport au milieu ($v$), suit l'équation
.
Par conséquent, la force totale est égale au produit de a masse corporelle ($m$) par a accélération ($a$), qui peut s'exprimer comme la variation de a vitesse par rapport au milieu ($v$) en fonction de temps ($t$), comme indiqué par l'étiquette
| $ m \displaystyle\frac{dv}{dt} = F_p - \displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
La force totale est égale à A force de propulsion ($F_p$), contrecarrée par a force de résistance ($F_W$) ainsi que a densité ($\rho$), le coefficient de résistance ($C_W$), le profil total de l'objet ($S_p$), et a vitesse par rapport au milieu ($v$) selon l'équation
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
,
ce qui conduit à l'équation suivante :
$F = F_p - \displaystyle\frac{1}{2} \rho S_w C_L v ^2$
Puisque la force totale est égale à A masse corporelle ($m$) multipliée par a accélération ($a$), et que cette dernière représente la variation de a vitesse par rapport au milieu ($v$) par rapport à temps ($t$), nous obtenons la suivante équation différentielle :
$F = m a = m \displaystyle\frac{dv}{dt}$
Cela conduit à l'équation différentielle :
| $ m \displaystyle\frac{dv}{dt} = F_p - \displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
.
.
ID:(14505, 0)
Accélération initiale
Équation
Au début du décollage, la résistance aérodynamique, qui dépend de la vitesse, est minimale. Par conséquent, a accélération maximale ($a_p$) est déterminée uniquement par a force de propulsion ($F_p$) et a masse corporelle ($m$) :
| $ a_p = \displaystyle\frac{ F_p }{ m }$ |
À mesure que la résistance aérodynamique commence à réduire la force de propulsion, cette accélération initiale sera maximale.
ID:(14506, 0)
Vitesse maximum
Équation
A force de propulsion ($F_p$) contrebalance a force de résistance ($F_W$) en générant de la vitesse, ce qui à son tour augmente la même force de résistance, comme décrit dans le profil total de l'objet ($S_p$), le coefficient de résistance ($C_W$), a densité ($\rho$) et a vitesse par rapport au milieu ($v$) dans
Ce processus continue d'augmenter la vitesse jusqu'au point où la force de propulsion équivaut à la force de résistance, ce qui représente la vitesse maximale atteignable.
En égalant la force de propulsion à la force de résistance et en résolvant pour la vitesse, nous obtenons a vitesse maximum ($v_p$) :
| $ v_p = \sqrt{\displaystyle\frac{2 F_p }{ \rho S_p C_W } }$ |
Si nous égalons a force de propulsion ($F_p$) avec a force de résistance ($F_W$) avec le profil total de l'objet ($S_p$), le coefficient de résistance ($C_W$), a densité ($\rho$) et a vitesse par rapport au milieu ($v$) dans
nous obtenons, pour un a vitesse maximum ($v_p$),
$F_p = \displaystyle\frac{1}{2} \rho S_w C_L v_p ^2$
ce qui, lorsqu'on le résout pour la vitesse maximale, donne
À mesure que la résistance aérodynamique commence à réduire la force de propulsion, cette accélération initiale sera maximale.
ID:(14507, 0)
Équation de vitesse de décollage
Équation
L'équation pour un avion décollant avec vitesse par rapport au milieu ($v$) peut être réécrite comme suit lorsqu'il décolle avec a densité ($\rho$), le profil total de l'objet ($S_p$), le coefficient de résistance ($C_W$), a masse corporelle ($m$), le temps ($t$) et a force de propulsion ($F_p$) :
Elle peut être réécrite avec a accélération maximale ($a_p$) et a vitesse maximum ($v_p$) comme suit :
| $\displaystyle\frac{dv}{dt}=a_p\left[1- \left(\displaystyle\frac{v}{v_p}\right)^2\right]$ |
L'équation pour un avion décollant avec vitesse par rapport au milieu ($v$) peut être réécrite comme suit lorsqu'il décolle avec a densité ($\rho$), le profil total de l'objet ($S_p$), le coefficient de résistance ($C_W$), a masse corporelle ($m$), le temps ($t$) et a force de propulsion ($F_p$) :
| $ m \displaystyle\frac{dv}{dt} = F_p - \displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
Cela peut être exprimé comme :
| $ a_p = \displaystyle\frac{ F_p }{ m }$ |
et a vitesse maximum ($v_p$)
| $ v_p = \sqrt{\displaystyle\frac{2 F_p }{ \rho S_p C_W } }$ |
comme suit :
| $\displaystyle\frac{dv}{dt}=a_p\left[1- \left(\displaystyle\frac{v}{v_p}\right)^2\right]$ |
ID:(15158, 0)
Vitesse de décollage
Équation
A vitesse par rapport au milieu ($v$) pour un avion qui décolle satisfait à l'équation avec a accélération maximale ($a_p$), a vitesse maximum ($v_p$) et le temps ($t$) :
| $\displaystyle\frac{dv}{dt}=a_p\left[1- \left(\displaystyle\frac{v}{v_p}\right)^2\right]$ |
Lorsqu'elle est intégrée dans la limite vitesse par rapport au milieu ($v$), bien inférieure à vitesse maximum ($v_p$), nous obtenons :
| $ v = \sqrt{ 2 a_p v_p t }$ |
A vitesse par rapport au milieu ($v$) pour un avion qui décolle satisfait à l'équation avec a accélération maximale ($a_p$), a vitesse maximum ($v_p$) et le temps ($t$) :
| $\displaystyle\frac{dv}{dt}=a_p\left[1- \left(\displaystyle\frac{v}{v_p}\right)^2\right]$ |
En intégrant, nous obtenons l'expression suivante :
$\log(v_p + v) + \log(v_p - v) = \displaystyle\frac{2 a_p}{v_p} t$
Si a vitesse par rapport au milieu ($v$) est bien plus petit que a vitesse maximum ($v_p$), les logarithmes peuvent être développés en une série de Taylor, ce qui conduit à une approximation du premier ordre :
| $ v = \sqrt{ 2 a_p v_p t }$ |
Généralement, la vitesse de décollage d'un avion est nettement inférieure à la vitesse maximale a vitesse maximum ($v_p$). Par conséquent, l'équation peut être résolue de manière analytique, comme expliqué dans le développement.
ID:(14508, 0)
Chemin emprunté au décollage
Équation
Étant donné que la vitesse au décollage, représentée par $v$, varie en fonction du temps $t$ selon l'équation
| $ v = \sqrt{ 2 a_p v_p t }$ |
nous pouvons calculer la distance parcourue le long de la piste en intégrant cette équation par rapport au temps :
| $ s = \sqrt{\displaystyle\frac{ 2^3 a_p v_p t ^3}{3^2}}$ |
Puisque la vitesse en fonction du temps est donnée par
| $ v = \sqrt{ 2 a_p v_p t }$ |
nous pouvons exprimer la vitesse comme le taux de changement de la distance par rapport au temps :
$\displaystyle\frac{ds}{dt} = \sqrt{2 a_p v_p t }$
Cette équation peut être intégrée, ce qui nous donne la relation entre la distance parcourue et le temps :
| $ s = \sqrt{\displaystyle\frac{ 2^3 a_p v_p t ^3}{3^2}}$ |
D'autre part, en tenant compte de la vitesse requise pour le décollage, nous pouvons déterminer le temps nécessaire pour l'atteindre, et en utilisant la distance parcourue, calculer la longueur de piste nécessaire pour le décollage.
ID:(14509, 0)
0
Video
Vidéo: Décoller et atterrir