Take off
Storyboard 
The key to taking off is to modify the wing in a way that achieves sufficient lift at lower speeds, allowing for a successful takeoff on a given runway length.
Variables
Calculations
Calculations
Equations
The lift force ($F_L$), along with the wing span ($L$), the density ($\rho$), the wing top speed factor ($c_t$), the wing bottom speed factor ($c_b$), the upper wing length ($l_t$), the bottom wing length ($l_b$), and the speed with respect to the medium ($v$), is found in
If we consider the surface that generates lift ($S_w$), given by the wing span ($L$), the upper wing length ($l_t$), and the bottom wing length ($l_b$),
and for the coefficient of lift ($C_L$), defined as
we obtain
The lift force ($F_L$) along with the density ($\rho$), the surface that generates lift ($S_w$), the coefficient of lift ($C_L$), and the speed with respect to the medium ($v$) is represented as
which, along with the body mass ($m$) and the gravitational Acceleration ($g$), must be equal to:
that is:
$\displaystyle\frac{1}{2}\rho S_wC_Lv^2=mg$
resulting in:
The coefficient of lift ($C_L$) is calculated with the body mass ($m$), the gravitational Acceleration ($g$), the surface that generates lift ($S_w$), the density ($\rho$), and the speed with respect to the medium ($v$) as follows:
Therefore, with the proportionality constant coefficient sustainability ($c$) and the angle of attack of a wing ($\alpha$),
we have
If we equate the propulsion force ($F_p$) with the resistance force ($F_W$) with the total object profile ($S_p$), the coefficient of resistance ($C_W$), the density ($\rho$), and the speed with respect to the medium ($v$) in
we obtain, for a the maximum speed ($v_p$),
$F_p = \displaystyle\frac{1}{2} \rho S_w C_L v_p ^2$
which, when solved for the maximum velocity, results in
The speed with respect to the medium ($v$) for an airplane taking off satisfies the equation with the maximum acceleration ($a_p$), the maximum speed ($v_p$), and the takeoff time ($t$):
Upon integration, we obtain the following expression:
$\log(v_p + v) - \log(v_p - v) - \log(v_p + v_0) + \log(v_p - v_0)= \displaystyle\frac{2 a_p}{v_p} t$
If the speed with respect to the medium ($v$) is much smaller than the maximum speed ($v_p$), the logarithms can be expanded into a Taylor series, resulting in a first-order approximation:
Since the velocity as a function of time is given by
we can express velocity as the rate of change of distance with respect to time:
$\displaystyle\frac{ds}{dt} = \sqrt{2 a_p v_p t }$
This equation can be integrated, yielding the relationship between the distance traveled and time:
Examples
The lift coefficient is a function of the angle of attack and typically follows the trend indicated in the following figure:
In the illustrated case, the slope is approximately 1.5 per 15 degrees, which corresponds to 0.1 1/degree or 5.73 1/radian.
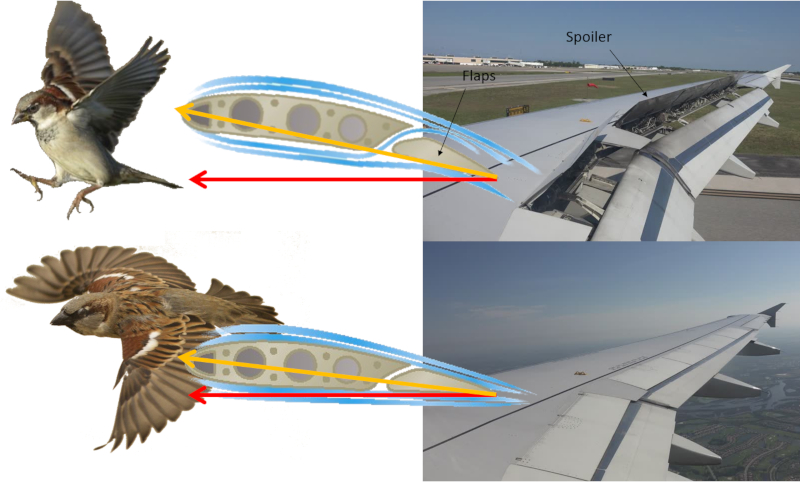
Both airplanes and birds can modify the shape of their wings. Airplanes achieve this through the use of flaps, while birds adjust the position of their primary and secondary feathers. This allows them to achieve high lift at low speeds during takeoff and landing, and a reduced lift coefficient at high speeds.
Additionally, airplanes are equipped with spoilers that assist in braking during landing.
In order for a spacecraft or a bird to remain in flight, the gravitational force ($F_g$) must counteract the force of gravity, which is defined by the body mass ($m$) and the gravitational Acceleration ($g$). In other words, it must be:
This is a simplified situation that does not take into account that the force of resistance can also generate a lift force.
To generate higher pressure below than above the wing and generate lift, Bernoulli's principle is employed, correcting for the lack of energy density conservation using ERROR:6119.1. The pressure over the wing, the lift force ($F_L$), can be estimated using the density ($\rho$), the surface that generates lift ($S_w$), the coefficient of lift ($C_L$), and the speed with respect to the medium ($v$) through the following formula:
The condition for achieving flight is met when the lift force ($F_L$) equals the weight of the aircraft or bird, which is calculated from the body mass ($m$) and the gravitational Acceleration ($g$). This is achieved with sufficient values of ERROR:6110,0, the surface that generates lift ($S_w$), and the coefficient of lift ($C_L$), where the latter coefficient is the adjustable factor. In the case of aircraft, pilots can modify the value of the coefficient of lift ($C_L$) using flaps, whose value must satisfy:
Flaps are adjusted by changing the angle that the wing makes with the direction of flight, known as the angle of attack.
From measurements, it is concluded that the lift coefficient $C_L$ is proportional to the angle of attack $\alpha$:
After a certain angle, the curve decreases until it reaches zero. This is because beyond that critical angle, the vortices fully cover the upper surface of the wing, leading to a loss of lift. This phenomenon is known as \"stall\".
Since the lift coefficient $C_L$ is proportional to the angle of attack $\alpha$, we can calculate the necessary angle to achieve sufficient lift for a given velocity $v$:
where $m$ is the mass, $g$ is the gravitational acceleration, $\rho$ is the density of the medium, $S_w$ is the wing area, and $c$ is the proportionality constant between the lift coefficient and the angle of attack.
If during takeoff an airplane with the number of engines ($n$) loses an engine, the propulsion force ($F_p$) decreases, which could mean the aircraft might not be able to take off and would be forced to abort the procedure. However, if the speed with respect to the medium ($v$) exceeds the new value of the maximum speed ($v_p$), it is possible to continue the takeoff safely. For this reason, the pilot monitors the parameters and informs the flying pilot once the aircraft has surpassed the so-called the critical speed $V2$ ($V2$), which is the critical speed calculated by:
The rotation speed $Vr$ ($Vr$) is reached when the airplane can take off by rotating to the necessary climb angle. In other words, it corresponds to the case where, with the values of the body mass ($m$), the gravitational Acceleration ($g$), the proportionality constant coefficient sustainability ($c$), the gravitational Acceleration ($g$), the total object profile ($S_p$), and the angle of attack of a wing ($\alpha$):
At the beginning of takeoff, aerodynamic resistance, which depends on velocity, is minimal. Therefore, the maximum acceleration ($a_p$) is determined solely by the propulsion force ($F_p$) and the body mass ($m$):
As aerodynamic resistance starts to reduce the propulsion force, this initial acceleration will be the maximum possible.
The propulsion force ($F_p$) counteracts the resistance force ($F_W$) by generating velocity, which in turn increases the same resistance force, as described in the total object profile ($S_p$), the coefficient of resistance ($C_W$), the density ($\rho$), and the speed with respect to the medium ($v$) in
This process continues to increase the velocity until the point where the propulsion force equals the resistance force, representing the maximum achievable speed.
By equating the propulsion force with the resistance force and solving for velocity, we obtain the maximum speed ($v_p$):
As aerodynamic resistance starts to reduce the propulsion force, this initial acceleration will be the maximum possible.
The speed with respect to the medium ($v$) for an airplane taking off satisfies the equation with the maximum acceleration ($a_p$), the maximum speed ($v_p$), and the takeoff time ($t$):
When integrated in the limit ERROR:6110,0 much smaller than ERROR:10075,0, we obtain:
Typically, the takeoff speed of an aircraft is significantly lower than the maximum speed the maximum speed ($v_p$). Therefore, the equation can be solved analytically, as explained in the development.
Since the takeoff velocity $v$ as a function of time $t$ is described by
we can calculate the distance traveled along the runway by integrating this equation with respect to time:
On the other hand, by considering the required takeoff velocity, we can determine the time needed to achieve it, and using the distance traveled, we can calculate the runway length required for takeoff.
ID:(1464, 0)