Planejar
Storyboard
Se o objeto (avião/ave) mantiver um ângulo de ataque ligeiramente negativo, pode fazer com que parte da força de sustentação contribua para impulsionar e contrariar a resistência. Desde que a força de sustentação restante não seja muito inferior à força da gravidade, o objeto pode permanecer no ar por um longo período. Isso pode ser chamado de um descente controlada extremamente lenta ou planagem.
ID:(466, 0)
Planejar
Descrição
Uma técnica de voo é conhecida como planar. Nesta técnica, as asas são usadas tanto para propulsão quanto para se manter no ar. Para alcançar isso, é essencial ajustar o ângulo de ataque da asa de forma que a força de sustentação compense a força gravitacional. Como resultado, o planar se torna uma descida controlada, na qual a descida é aproveitada para gerar sustentação e, assim, reduzir a velocidade de maneira controlada.
ID:(1171, 0)
Forças ao voar
Descrição
A chave para planar é inclinar a aeronave ou ave para a frente, ou seja, ter um ângulo negativo representado por aceleração máxima ($\alpha$). Com esse ângulo negativo, o vetor la força de elevação ($F_L$) aponta para cima e para frente em vez de para trás. Isso resulta em uma força de tração em vez de la força de resistência ($F_W$), impulsionando a aeronave ou ave e gerando velocidade, o que, por sua vez, cria a sustentação necessária.

Esse mecanismo permite o voo, mas é essencial entender que é essencialmente uma descida lenta e controlada, uma vez que não se alcança um uma força de elevação ($F_L$) vertical que compense completamente o próprio peso. Portanto, é necessário levar a planadora a altas altitudes ou permitir que a ave ganhe altura inicialmente por meio de sua própria propulsão. Em seguida, ambos procuram correntes ascendentes que lhes permitem planar dentro de uma corrente ascendente mais forte do que a velocidade de descida da planadora. Dessa forma, eles podem permanecer em voo por longos períodos sem a necessidade de aterrissar.
ID:(7044, 0)
Ângulo de deslizamento
Descrição
Da mesma forma que o aceleração máxima ($\alpha$) é definido como o ângulo entre a linha central da asa e o horizonte, seu equivalente negativo pode ser definido como o ângulo de deslizamento ($\phi$).

Planador Jonker JS3 Rapture (Air Cargo Week)
ID:(7047, 0)
Forças em deslizamento
Descrição
No caso das forças, temos as seguintes ações:
• la força de elevação ($F_L$) age perpendicularmente ao eixo da aeronave ou ave.
• la força de resistência ($F_W$) age ao longo do eixo da aeronave ou ave.
• la força gravitacional ($F_g$) ($mg$) age verticalmente.
Essas três forças são representadas no centro do diagrama:
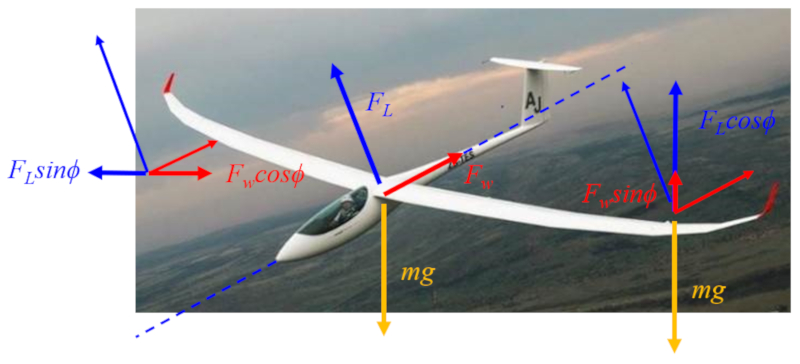
Planador Jonker JS3 Rapture (Air Cargo Week)
No lado esquerdo, pode-se observar a componente horizontal, onde a sustentação contraria o arrasto, atuando como impulso.
No lado direito, são visíveis as componentes verticais, onde ambas as forças aerodinâmicas (sustentação e arrasto) se opõem ao peso que age sobre o centro de massa.
Embora as forças se anulem entre si, o planador desce porque sua direção de voo é determinada pelo ângulo de planagem.
ID:(7046, 0)
Equação de deslizamento horizontal
Equação
No caso do planar, o objetivo é manter uma velocidade constante, o que significa que la força de elevação ($F_L$) deve gerar propulsão suficiente para contrariar la força de resistência ($F_W$).
Para alcançar este força de elevação ($F_L$), a ave ou a aeronave gera um um aceleração máxima ($\alpha$) negativo, o que significa que parte de la força de elevação ($F_L$) se converte em força de propulsão. Esta componente de força é igual ao seno do ângulo.
A inclinação também leva a uma redução em la força de resistência ($F_W$), uma vez que parte dela contribui para a sustentação. Neste caso, a componente que ainda contribui para a resistência é esta força multiplicada pelo cosseno do ângulo.
Portanto, a equação de força no plano horizontal pode ser expressa como:
Em vez de usar o aceleração máxima ($\alpha$), trabalharemos com o ângulo de deslizamento ($\phi$).
ID:(4420, 0)
Equação de deslizamento vertical
Equação
No plano vertical, o ângulo de deslizamento ($\phi$) resulta em uma redução de la força de elevação ($F_L$) por um fator igual ao cosseno do ângulo. Por outro lado, faz com que la força de resistência ($F_W$) contribua com a sustentação com um fator igual ao seno do ângulo. Ambas as forças devem contrabalançar o peso gerado por la massa do objeto ($m$) e la aceleração gravitacional ($g$), então temos:
ID:(4419, 0)
Força de elevação deslizante
Equação
Vamos considerar la força de elevação ($F_L$), la força de resistência ($F_W$), la massa do objeto ($m$), la aceleração gravitacional ($g$) e o ângulo de deslizamento ($\phi$).
Se analisarmos as forças durante o planeio na direção vertical:
| $ F_L \cos \phi + F_w \sin \phi = m g $ |
e na direção horizontal:
| $ F_L \sin \phi = F_w \cos \phi $ |
podemos resolver o sistema de equações para obter la força de elevação ($F_L$):
Se considerarmos la força de elevação ($F_L$), la força de resistência ($F_W$), la massa do objeto ($m$), la aceleração gravitacional ($g$) e o ângulo de deslizamento ($\phi$), a força durante o planeio na direção vertical é:
| $ F_L \cos \phi + F_w \sin \phi = m g $ |
e na direção horizontal é:
| $ F_L \sin \phi = F_w \cos \phi $ |
Isso nos permite eliminar la força de resistência ($F_W$), resultando em:
$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$
Portanto, la força de elevação ($F_L$) é:
| $ F_L = m g \cos\phi $ |
ID:(4421, 0)
Força de arrasto deslizante
Equação
Vamos considerar la força de elevação ($F_L$), la força de resistência ($F_W$), la massa do objeto ($m$), la aceleração gravitacional ($g$) e o ângulo de deslizamento ($\phi$).
Se analisarmos as forças durante o planeio na direção vertical:
| $ F_L \cos \phi + F_w \sin \phi = m g $ |
e na direção horizontal:
| $ F_L \sin \phi = F_w \cos \phi $ |
podemos resolver o sistema de equações para obter la força de resistência ($F_W$):
Se considerarmos la força de elevação ($F_L$), la força de resistência ($F_W$), la massa do objeto ($m$), la aceleração gravitacional ($g$) e o ângulo de deslizamento ($\phi$), a força durante o planeio na direção vertical é:
| $ F_L \cos \phi + F_w \sin \phi = m g $ |
e na direção horizontal é:
| $ F_L \sin \phi = F_w \cos \phi $ |
Isso nos permite eliminar la força de elevação ($F_L$), resultando em:
$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$
la força de resistência ($F_W$) deve ser:
| $ F_W = m g \sin \phi $ |
ID:(4422, 0)
Ângulo de deslizamento
Equação
La força de elevação ($F_L$) e la força de resistência ($F_W$) dependem de la massa do objeto ($m$), la aceleração gravitacional ($g$), e o ângulo de deslizamento ($\phi$). Ambas as equações nos permitem calcular o ângulo de deslizamento ($\phi$) em termos de la força de elevação ($F_L$) e la força de resistência ($F_W$).
Uma vez que la força de elevação ($F_L$) e la força de resistência ($F_W$) são funções de la massa do objeto ($m$), la velocidade em relação ao meio ($v$), la superfície que gera sustentação ($S_w$), o perfil total do objeto ($S_p$), o coeficiente de elevação ($C_L$) e o coeficiente de resistência ($C_W$), podemos demonstrar que o ângulo de deslizamento ($\phi$) é:
Vamos considerar la força de elevação ($F_L$), la força de resistência ($F_W$), la massa do objeto ($m$), la aceleração gravitacional ($g$) e o ângulo de deslizamento ($\phi$). Com essas forças, a força de sustentação é calculada da seguinte forma:
| $ F_L = m g \cos\phi $ |
e a força de arrasto como:
| $ F_W = m g \sin \phi $ |
Podemos determinar o ângulo de deslizamento ($\phi$) dividindo la força de elevação ($F_L$) por la força de resistência ($F_W$), resultando em:
$\tan\phi=\displaystyle\frac{F_W}{F_L}$
Onde la força de resistência ($F_W$) é calculado usando a seguinte equação:
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
com o perfil total do objeto ($S_p$) e o coeficiente de resistência ($C_W$). Da mesma forma, la força de elevação ($F_L$) é calculado da seguinte forma:
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
com la superfície que gera sustentação ($S_w$) e o coeficiente de elevação ($C_L$).
Com ambas as forças, podemos determinar o ângulo de ataque necessário para o planador da seguinte forma:
| $ \tan \phi =\displaystyle\frac{ S_p C_w }{ S_w C_L }$ |
ID:(4423, 0)
0
Video
Vídeo: Plano
