Storyboard

Para voar a uma altitude constante, o objeto (avião/ave) deve ajustar o ângulo de ataque da asa de forma a contrabalançar o peso com a propulsão e manter a velocidade desejada.

>Modelo

ID:(1463, 0)

Iframe

>Top

ID:(15169, 0)

Conceito

>Top

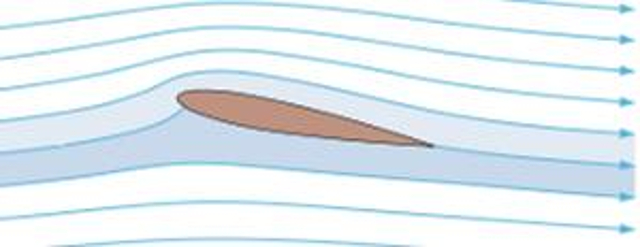
Se assumirmos que o fluxo ao redor de uma asa é laminar, podemos observar várias camadas que cercam a asa. Aquelas na parte superior tendem a ser um pouco mais longas devido à curvatura para cima, enquanto as camadas inferiores tendem a ser mais curtas e, portanto, mais próximas à asa.

Supondo que o fluxo seja tal que essas camadas convergem de modo que pontos próximos um do outro em ambos os lados da asa retornem à mesma posição relativa quando o fluxo se separa, a velocidade das camadas superiores será necessariamente maior do que a das camadas inferiores. É importante lembrar que esta é apenas uma suposição, e não há uma real necessidade de que elas convergam; na verdade, elas podem acabar desalinhadas sem nenhum problema.

ID:(7016, 0)

Conceito

>Top

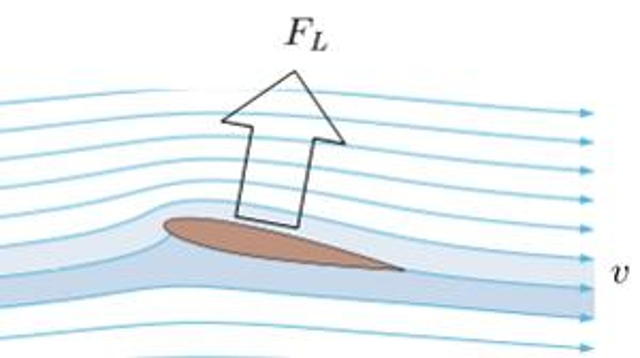
Uma vez que a velocidade nas camadas superiores da asa é maior do que nas camadas inferiores, isso implica que a pressão na parte superior da asa é menor do que na parte inferior.

Isso significa efetivamente que há uma força maior de baixo da asa do que de cima da asa, o que resulta na geração de uma força de sustentação.

ID:(7018, 0)

Conceito

>Top

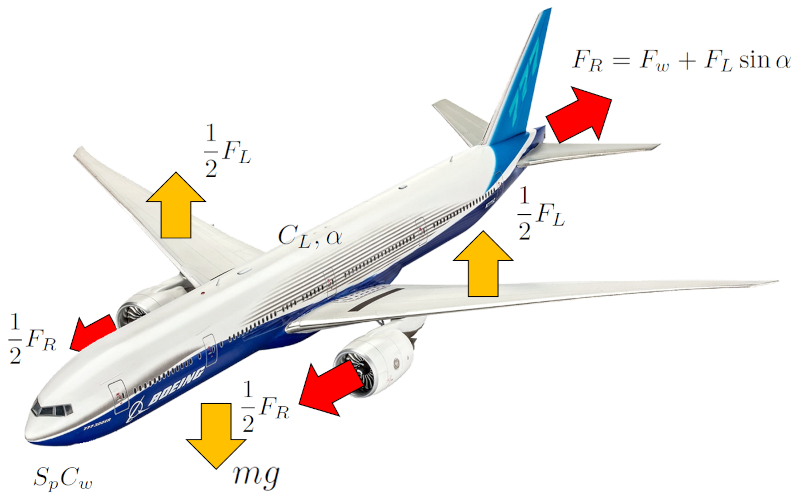
As forças que influenciam uma aeronave ou ave podem ser categorizadas em dois grupos fundamentais:

Forças que afetam o controle do movimento do centro de massa:

• la força de elevação ($F_L$), que contraria la força gravitacional ($F_g$).
• la força de propulsão ($F_p$), que se opõe a la força de resistência ($F_W$).

Forças destinadas a alcançar a rotação da aeronave ou ave em torno do centro de massa, obtidas por meio dos ailerons nas asas e do leme de direção:

• Os ailerons permitem gerar um momento de torção ao alterar de forma assimétrica a sustentação em cada asa.
• O leme controla a direção da aeronave ou ave redirecionando o fluxo de ar.

Boeing Images - 777-300ER Illustration in Boeing Livery

Parâmetros-chave para controlar o movimento do centro de massa são:

• la superfície que gera sustentação ($S_w$) e o perfil total do objeto ($S_p$).
• o coeficiente de elevação ($C_L$) e o coeficiente de resistência ($C_W$), sendo que este último depende de o aceleração máxima ($\alpha$).

ID:(11080, 0)

Top

>Top

Parâmetros

$g$

g

Aceleração gravitacional

m/s^2

$C_W$

C_W

Coeficiente de resistência

-

$c$

c

Constante de proporcionalidade do coeficiente de sustentação

1/rad

$\rho$

rho

Densidade

kg/m^3

$m$

m

Massa corporal

kg

$S_p$

S_p

Perfil total do objeto

m^2

$S_w$

S_w

Superfície que gera sustentação

m^2

Variáveis

$\alpha_s$

alpha_s

Ângulo necessário para elevação

rad

$C_L$

C_L

Coeficiente de elevação

-

$F_L$

F_L

Força de elevação

N

$F_W$

F_W

Força de resistência

N

$F_R$

F_R

Força de resistência total

N

$F_g$

F_g

Força gravitacional

N

$P$

P

Perfil total do objeto

W

$v$

v

Velocidade em relação ao meio

m/s

Cálculos

• Método alternativo
• Método tradicional
• Estratégia
• 2D
• 3D

Equação

Equação

Primeiro, selecione a equação: para , depois, selecione a variável: para

---

Cálculos

Símbolo

Equação

Resolvido

Traduzido

Cálculos

Símbolo

Equação

Resolvido

Traduzido

Variáve Dado Calcular Objetivo : Equação A ser usado

Equações

ID:(15170, 0)

Equação

>Top, >Modelo

La força gravitacional ($F_g$) baseia-se em la massa gravitacional ($m_g$) do objeto e em uma constante que reflete a intensidade da gravidade na superfície do planeta. Esta última é identificada por la aceleração gravitacional ($g$), que é igual a $9.8 m/s^2$.

Consequentemente, conclui-se que:

$F_g = m g$

$F_g = m_g g$

Condições

Variáveis

$g$

Aceleração gravitacional

9.8

$m/s^2$

5310

$F_g$

Força gravitacional

$N$

4977

$m_g$

$m$

Massa corporal

$kg$

6150

Relação

ID:(3241, 0)

Equação

>Top, >Modelo

Para gerar uma pressão maior abaixo do que acima da asa e gerar sustentação, utiliza-se o princípio de Bernoulli, corrigindo a falta de conservação da densidade de energia com um coeficiente de elevação ($C_L$). A pressão sobre a asa, la força de elevação ($F_L$), pode ser estimada usando la densidade ($\rho$), la superfície que gera sustentação ($S_w$), o coeficiente de elevação ($C_L$) e la velocidade em relação ao meio ($v$) através da seguinte fórmula:

$F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$

Condições

Variáveis

$C_L$

Coeficiente de elevação

$-$

6164

$\rho$

Densidade

$kg/m^3$

5342

$F_L$

Força de elevação

$N$

6120

$S_w$

Superfície que gera sustentação

$m^2$

6117

$v$

Velocidade em relação ao meio

$m/s$

6110

Relação

Desenvolvimento

La força de elevação ($F_L$), juntamente com la envergadura das asas ($L$), la densidade ($\rho$), o fator de velocidade máxima da asa ($c_t$), o fator de velocidade inferior da asa ($c_b$), la comprimento superior da asa ($l_t$), la comprimento inferior da asa ($l_b$) e la velocidade em relação ao meio ($v$), encontra-se em

$F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$

Se considerarmos la superfície que gera sustentação ($S_w$), definido por la envergadura das asas ($L$), la comprimento superior da asa ($l_t$) e la comprimento inferior da asa ($l_b$),

$S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$

e para o coeficiente de elevação ($C_L$), definido como

$C_L = 4\displaystyle\frac{ c_t l_t - c_b l_b }{ l_t + l_b }$

obtemos

$F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$

ID:(4417, 0)

Equação

>Top, >Modelo

Para calcular la força de resistência total ($F_R$), assumimos ângulos pequenos e consideramos uma situação na qual o ângulo é tal que mantém la massa corporal ($m$). Usando esta aproximação e as variáveis o coeficiente de elevação ($C_L$), o coeficiente de resistência ($C_W$), la superfície que gera sustentação ($S_w$), o perfil total do objeto ($S_p$), la aceleração gravitacional ($g$), la constante de proporcionalidade do coeficiente de sustentação ($c$), la densidade ($\rho$) e la velocidade em relação ao meio ($v$), obtemos a seguinte expressão:

$F_R = \displaystyle\frac{1}{2} \rho S_p C_w v ^2 + \displaystyle\frac{2 m ^2 g ^2}{ c ^2 S_w \rho }\displaystyle\frac{1}{ v ^2}$

Condições

Variáveis

$g$

Aceleração gravitacional

9.8

$m/s^2$

5310

$C_w$

Coeficiente de resistência

$-$

6122

$c$

Constante de proporcionalidade do coeficiente de sustentação

$1/rad$

6165

$\rho$

Densidade

$kg/m^3$

5342

$F_R$

Força de resistência total

$N$

8480

$m$

Massa corporal

$kg$

6150

$S_p$

Perfil total do objeto

$m^2$

6123

$S_w$

Superfície que gera sustentação

$m^2$

6117

$v$

Velocidade em relação ao meio

$m/s$

6110

Relação

Desenvolvimento

Utilizando as relações de la força de resistência total ($F_R$) com la força de elevação ($F_L$), la força de resistência ($F_W$) e o aceleração máxima ($\alpha$):

$F_R = F_W \cos \alpha + F_L \sin \alpha$

podemos calcular a força de resistência utilizando la densidade ($\rho$), o coeficiente de resistência ($C_W$), o perfil total do objeto ($S_p$) e la velocidade em relação ao meio ($v$):



e a força de sustentação com la superfície que gera sustentação ($S_w$) e o coeficiente de elevação ($C_L$):



utilizando a relação para o coeficiente de elevação ($C_L$) com la constante de proporcionalidade do coeficiente de sustentação ($c$):



usando a relação para o seno do pequeno ângulo de ataque $\alpha$:



e o cosseno:



com a condição de equilibrar o peso do pássaro ou aeronave para la massa corporal ($m$) e la aceleração gravitacional ($g$):



obtemos:

ID:(4546, 0)

Equação

>Top, >Modelo

A força total de resistência é composta pelas componentes horizontais da força de resistência do perfil da asa $F_W$ e da força de sustentação $F_L$, que podem ser calculadas a partir do ângulo de ataque $\alpha$:

$F_R = F_W \cos \alpha + F_L \sin \alpha$

Condições

Variáveis

$\alpha$

Ângulo necessário para elevação

$rad$

6167

$F_L$

Força de elevação

$N$

6120

$F_w$

Força de resistência

$N$

6124

$F_R$

Força de resistência total

$N$

8480

Relação

Desenvolvimento

A componente horizontal da sustentação corresponde à força $F_L$ multiplicada pelo seno do ângulo de ataque $\alpha$:

$F_L \sin\alpha$

e a componente horizontal da resistência corresponde à força $F_W$ multiplicada pelo cosseno do ângulo de ataque $\alpha$:

$F_W \cos\alpha$

Portanto, a força total de resistência é calculada da seguinte forma:

$F_R = F_W \cos \alpha + F_L \sin \alpha$

ID:(9579, 0)

Equação

>Top, >Modelo

La força de resistência ($F_W$) pode ser calculado usando la densidade ($\rho$), o coeficiente de resistência ($C_W$), o perfil total do objeto ($S_p$) e la velocidade em relação ao meio ($v$) de acordo com o seguinte fórmula:

$F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$

Condições

Variáveis

$C_W$

Coeficiente de resistência

$-$

6122

$\rho$

Densidade

$kg/m^3$

5342

$F_W$

Força de resistência

$N$

6124

$S_p$

Perfil total do objeto

$m^2$

6123

$v$

Velocidade em relação ao meio

$m/s$

6110

Relação

Desenvolvimento

De maneira semelhante à forma como a equação para la força de elevação ($F_L$) foi obtida utilizando la densidade ($\rho$), o coeficiente de elevação ($C_L$), la superfície que gera sustentação ($S_w$) e la velocidade em relação ao meio ($v$)

$F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$

nesta analogia, o que corresponde a la superfície que gera sustentação ($S_w$) será equivalente a o perfil total do objeto ($S_p$) e o coeficiente de elevação ($C_L$) a o coeficiente de resistência ($C_W$), resultando no cálculo de la força de resistência ($F_W$):

$F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$

O coeficiente de arrasto é medido e, em fluxos turbulentos sobre corpos aerodinâmicos, geralmente se obtêm valores em torno de 0.4.

ID:(4418, 0)

Equação

>Top, >Modelo

La potencia $P$ é a energia por unidade de tempo necessária para manter uma força $F_R$ constante. Portanto, ela pode ser calculada multiplicando essa força pela velocidade $v$:

$P = F_R v$

Condições

Variáveis

$F_R$

Força de resistência total

$N$

8480

$P$

Perfil total do objeto

$W$

6331

$v$

Velocidade em relação ao meio

$m/s$

6110

Relação

Desenvolvimento

A potência é definida como a energia $\Delta W$ por tempo $\Delta t$, de acordo com a equação:



Uma vez que a energia é igual à força $F$ multiplicada pela distância percorrida $\Delta s$, temos:



Assim, obtemos:

$P=\displaystyle\frac{\Delta W}{\Delta t}= F_R \displaystyle\frac{\Delta s}{\Delta t}$

No entanto, dado que a distância percorrida em um intervalo de tempo é a velocidade $v$:

$\bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$

Finalmente, podemos escrever a expressão da potência como:

$P = F_R v$

ID:(4547, 0)

Equação

>Top, >Modelo

Para obter la perfil total do objeto ($P$), é necessário multiplicar la força de resistência total ($F_R$) por la velocidade em relação ao meio ($v$). Uma vez que la força de resistência total ($F_R$) é uma função de la densidade ($\rho$), la superfície que gera sustentação ($S_w$), o perfil total do objeto ($S_p$), o coeficiente de resistência ($C_W$), la constante de proporcionalidade do coeficiente de sustentação ($c$), la massa corporal ($m$) e la aceleração gravitacional ($g$), que é igual a

,

o potencial é

$P =\displaystyle\frac{1}{2} \rho S_p C_W v ^3 + \displaystyle\frac{2 m ^2 g ^2}{ c ^2 S_w \rho }\displaystyle\frac{1}{ v }$

Condições

Variáveis

$g$

Aceleração gravitacional

9.8

$m/s^2$

5310

$C_w$

Coeficiente de resistência

$-$

6122

$c$

Constante de proporcionalidade do coeficiente de sustentação

$1/rad$

6165

$\rho$

Densidade

$kg/m^3$

5342

$m$

Massa corporal

$kg$

6150

$S_p$

Perfil total do objeto

$m^2$

6123

$P$

Perfil total do objeto

$W$

6331

$S_w$

Superfície que gera sustentação

$m^2$

6117

$v$

Velocidade em relação ao meio

$m/s$

6110

Relação

Desenvolvimento

La força de resistência total ($F_R$) é uma função de la densidade ($\rho$), la superfície que gera sustentação ($S_w$), o perfil total do objeto ($S_p$), o coeficiente de resistência ($C_W$), la constante de proporcionalidade do coeficiente de sustentação ($c$), la massa corporal ($m$) e la aceleração gravitacional ($g$), o que é igual a

,

portanto, usando a equação para la perfil total do objeto ($P$)

,

obtemos:

.

.

ID:(4548, 0)