Utilizador:
Força e torque
Descrição
Como vimos, o torque desempenha um papel análogo ao da força no caso da rotação:
$F\longleftrightarrow T$
Para estabelecer as equações de movimento, podemos lembrar como a força foi definida em termos de momento:
$F=\displaystyle\frac{\Delta p}{\Delta t}$
e como o torque foi definido:
$T=\displaystyle\frac{\Delta L}{\Delta t}$
Podemos estabelecer uma relação entre os dois para descrever a geração de torque com base na força:
Portanto, devemos primeiro definir o que equivale ao Momento no contexto da rotação.
ID:(325, 0)
Torque simples - relação de força
Equação
Dado que a relação entre o momento angular e o torque é
| $ L = r p $ |
sua derivada temporal nos leva à relação do torque
 $ T = r F $ |
A rotação do corpo ocorre em torno de um eixo na direção do torque, que passa pelo centro de massa.
ID:(4431, 0)
Lei da Alavanca
Equação
Uma vez que o torque gerado pela força gravitacional e pelo braço da alavanca é
| $ T = r F $ |
em cada lado da balança, no caso de equilíbrio, ele deve se anular para que haja equilíbrio:
Isso é expresso matematicamente como:
| $ d_1 F_1 = d_2 F_2 $ |
No caso de uma balança, atua sobre cada braço uma força gravitacional que gera um torque
| $ T = r F $ |
Se o comprimento dos braços for $d_i$ e as forças forem $F_i$ com $i=1,2$, a condição de equilíbrio exige que a soma dos torques seja zero:
| $\displaystyle\sum_i \vec{T}_i=0$ |
Portanto, considerando que o sinal de cada torque depende da direção em que está induzindo a rotação,
$d_1F_1-d_2F_2=0$
o que resulta em
| $ d_1 F_1 = d_2 F_2 $ |
.
ID:(3250, 0)
Conceito de centro de massa (CM)
Imagem
Se considerarmos a distribuição de massa no espaço, deverá sempre ser possível identificar um ponto onde a força exercida pela massa de um lado seja igual à força gerada no outro lado:
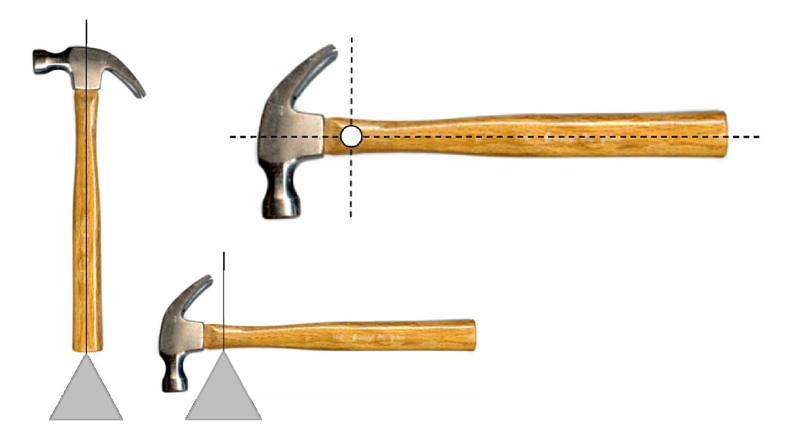
Esse conceito implica que, para qualquer orientação de um objeto, é possível localizar um ponto de apoio no qual o objeto esteja em equilíbrio. Cada um desses pontos corresponde a uma linha vertical. Ao repetir esse processo com diferentes orientações do objeto, eventualmente fica evidente que as linhas verticais se cruzam em um ponto específico dentro do objeto. Esse ponto é denominado centro de massa (CM). Em essência, o centro de massa é o ponto único dentro do objeto onde, independentemente de sua orientação, o equilíbrio é sempre alcançado.
ID:(323, 0)
Definição do centro de massa (CM)
Imagem
Pode-se definir o centro de massa como o ponto em que todas as linhas verticais traçadas através dos pontos onde o sistema está em equilíbrio se intersectam:
ID:(11603, 0)
Equilíbrio de Rotação
Equação
Quando um corpo está em equilíbrio em relação à rotação, ele não gira em torno de seu centro de massa. Para isso, a soma dos torques atuando sobre ele deve ser zero. Isso implica que:
| $\displaystyle\sum_i \vec{T}_i=0$ |
ID:(10754, 0)
Centro de massa
Equação
Se observarmos um corpo que é sustentado a partir de um ponto, perceberemos a necessidade de equilibrá-lo cuidadosamente para evitar que ele role em uma direção ou outra. Isso nos leva à ideia de que existe um ponto a partir do qual o corpo pode ser equilibrado sem rotação.
Esse ponto é chamado de centro de massa.
Para determinar o ponto de equilíbrio, podemos equilibrar o objeto ao longo de cada um de seus eixos. Ao orientá-lo de uma certa maneira e encontrar a posição em que ele permanece equilibrado, identificamos uma linha imaginária na qual se encontra o centro de massa.
Uma vez que uma das coordenadas do centro de massa tenha sido determinada, o objeto é girado para encontrar a próxima coordenada do centro de massa.
Dessa maneira, um ponto conhecido como centro de massa é determinado, e ele pode ser calculado através de:
| $ \vec{r}_{CM} =\displaystyle\frac{\displaystyle\sum_i m_i \vec{r}_i }{\displaystyle\sum_i m_i }$ |
Se tivermos várias massas $m_i$, cada uma estará sujeita a uma força gravitacional
| $ F_g = m_g g $ |
gerando um torque igual a
| $ T = r F $ |
onde $r_i$ é a distância horizontal da massa $i$ ao ponto de apoio. O torque total será
$T=\displaystyle\sum_iT_i$
Se $r_{CM}$ for a posição do centro de massa, o torque total em torno deste ponto
$T_{CM}=\displaystyle\sum_i T_i=\displaystyle\sum_i(r_i-r_{CM})m_ig=0$
deve ser igual a zero. A partir desta equação, podemos resolver para encontrar a posição do centro de massa, resultando em
| $ \vec{r}_{CM} =\displaystyle\frac{\displaystyle\sum_i m_i \vec{r}_i }{\displaystyle\sum_i m_i }$ |
.
.
ID:(3248, 0)
Trajetória de um corpo com translação e rotação
Imagem
Qualquer objeto que se desloque e gire o faz de tal maneira que:
• seu movimento de translação pode ser descrito como se toda a massa estivesse concentrada no centro de massa,
• sua rotação ocorre em torno do centro de massa como se não estivesse em deslocamento.
ID:(11604, 0)
Torque (vetor)
Equação
O torque é representado como um vetor na direção do eixo de rotação. Como o raio de rotação e a força são ortogonais entre si, a relação é
| $ T = r F $ |
Isso pode ser expresso como o produto cruz entre a velocidade angular e o raio:
| $ \vec{T} = \vec{r} \times \vec{F} $ |
Uma vez que a magnitude do torque é
| $ T = r F $ |
Se o vetor do eixo é
$\hat{n}=\hat{r}\times\hat{t}$
Portanto, considerando que
$\vec{F} =F\hat{t}$
,
$\vec{r} =r\hat{r}$
,
$\vec{T}=T\hat{n}$
temos que
$\vec{T} =T\hat{n}=T\hat{r}\times\hat{t}=rF\hat{r}\times\hat{t}=\vec{r}\times\vec{F}$
o que significa
| $ \vec{T} = \vec{r} \times \vec{F} $ |
ID:(3249, 0)
Torque, regra da mão direita
Imagem
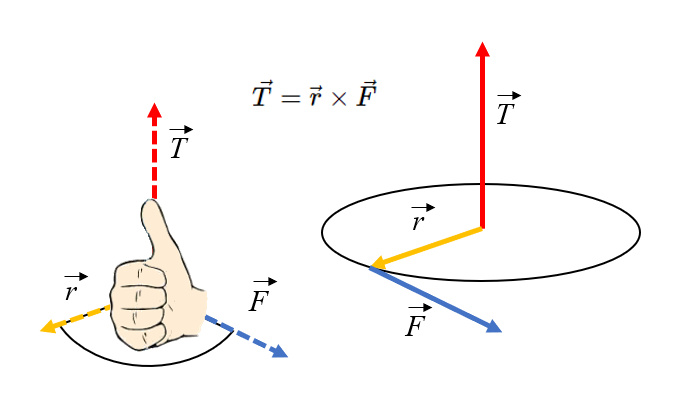
A orientação do torque pode ser determinada usando a regra da mão direita: se você apontar os dedos na direção do raio e girar na direção da força,
ID:(11602, 0)
0
Video
Vídeo: Geração de Torque