Utilizador:
Inércia rotacional
Video
Se considerarmos um objeto com um momento de inércia $I$ e uma velocidade angular $\omega$, podemos observar que existem duas situações em que mudar seu movimento é mais desafiador:
• Quando o momento de inércia é muito grande (por exemplo, tentar parar um carrossel).
• Quando a velocidade angular é muito alta (por exemplo, tentar parar o eixo de um motor).
Por isso, é introduzida uma medida de movimento que envolve o corpo, que é o produto do momento de inércia com a velocidade angular, conhecido como momento angular do corpo.
No balé, é possível ver como a bailarina aplica o primeiro princípio de Newton para a rotação em todas as suas piruetas:
ID:(10284, 0)
Momento angular constante
Equação
Se o momento angular é constante, sua relação proporcional com a velocidade angular leva à conclusão de que a variação do ângulo é proporcional à variação do tempo.
 $ L \Delta t = m r ^2 \Delta\theta $ |
Uma vez que o momento angular é igual a
| $ L = I \omega $ |
e o momento de inércia é
| $ I = m r ^2$ |
usando
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
conclui-se que
| $ L \Delta t = m r ^2 \Delta\theta $ |
Considerando que o aumento do ângulo multiplicado pelo raio resulta no comprimento do arco, e o comprimento do arco multiplicado pelo raio é o dobro da área do triângulo formado pelo corpo em rotação,
$\Delta S = \displaystyle\frac{1}{2} r r \Delta\theta$
isso leva à segunda lei de Kepler:
Segunda Lei de Kepler: Planetas varrem áreas iguais em tempos iguais ao longo de suas órbitas.
Se levarmos em conta a primeira lei de Kepler:
Primeira Lei de Kepler: Planetas orbitam em órbitas elípticas (=com formato de elipse) onde o sol está localizado em um dos focos.
conclui-se que um planeta é mais rápido quando se aproxima do sol (solstício de verão no hemisfério sul) do que quando está no ponto mais distante de sua órbita (solstício de inverno no hemisfério sul):
ID:(10282, 0)
Momento angular e momento
Equação
Em uma dimensão, o momento angular ($L$) juntamente com la braço ($r$) e o momento ($p$) é igual a
| $ L = r p $ |
o momento angular ($L$) pode ser generalizado para mais dimensões como la momento Angular (Vetorial) ($vec{L}$). Como ambos os parâmetros la raio (vetor) ($\vec{r}$) e ($$) são vetoriais, a definição de la momento Angular (Vetorial) ($vec{L}$) é construída através de um produto cruzado na forma:
| $ \vec{L} = \vec{r} \times \vec{p} $ |
ID:(4774, 0)
Momento angular, regra da mão direita
Imagem
A orientação do momento angular pode ser determinada usando a regra da mão direita: se você apontar seus dedos na direção do raio e girar na direção do momento,
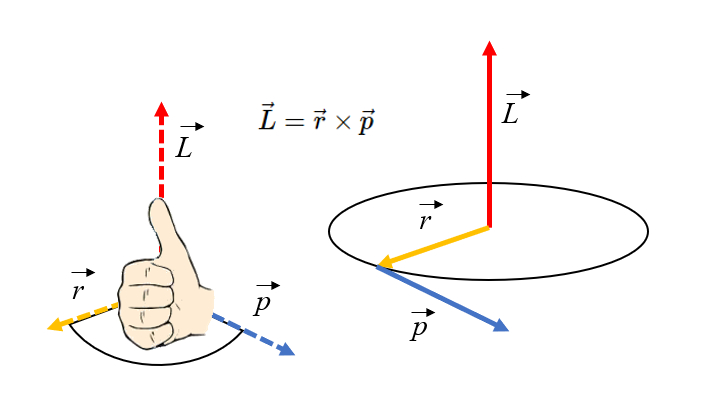
ID:(11601, 0)
0
Video
Vídeo: Inércia Rotacional