Benützer:
Drehmoment-Erzeugung
Storyboard 
Das Drehmoment wird durch eine Kraft erzeugt, die in einem bestimmten Abstand von der Drehachse aufgebracht wird. Kräfte auf einen Punkt auf der Rotationsachse führen nur zur Translation und nicht zu Änderungen der Rotation oder des Drehmoments.
Der kürzeste Abstand zwischen dem Punkt, der die Kraft angreift, und der Achse wird als Arm bezeichnet und ist immer senkrecht zur Achse. Eine Kraft parallel zum Arm erzeugt nur eine Wellenverschiebung, so dass nur die Kräfte senkrecht zum Arm ein Drehmoment erzeugen.
Schließlich ist zu sehen, dass das Drehmoment umso größer ist, je größer der Arm und je größer die Kraft senkrecht zum Arm ist.
ID:(1416, 0)
Kraft und Drehmoment
Definition
Wie wir gesehen haben, erfüllt das Drehmoment eine analoge Rolle zur Kraft im Falle der Rotation:
$F\longleftrightarrow T$
Um die Bewegungsgleichungen aufzustellen, können wir uns daran erinnern, wie die Kraft in Bezug auf den Impuls definiert wurde:
$F=\displaystyle\frac{\Delta p}{\Delta t}$
und wie das Drehmoment definiert wurde:
$T=\displaystyle\frac{\Delta L}{\Delta t}$
Wir können eine Beziehung zwischen beiden herstellen, um die Erzeugung von Drehmoment aufgrund von Kraft zu beschreiben:
Daher müssen wir zunächst definieren, was dem Impuls im Kontext der Rotation entspricht.
ID:(325, 0)
Drehmoment-Erzeugung
Beschreibung
Das Drehmoment wird durch eine Kraft erzeugt, die in einem bestimmten Abstand von der Drehachse aufgebracht wird. Kräfte auf einen Punkt auf der Rotationsachse führen nur zur Translation und nicht zu Änderungen der Rotation oder des Drehmoments. Der kürzeste Abstand zwischen dem Punkt, der die Kraft angreift, und der Achse wird als Arm bezeichnet und ist immer senkrecht zur Achse. Eine Kraft parallel zum Arm erzeugt nur eine Wellenverschiebung, so dass nur die Kräfte senkrecht zum Arm ein Drehmoment erzeugen. Schließlich ist zu sehen, dass das Drehmoment umso größer ist, je größer der Arm und je größer die Kraft senkrecht zum Arm ist.
Variablen
Berechnungen
zu 
,
dann die Variable auswählen: 
zu 
Berechnungen
Variable
Gegeben
Berechnen
Ziel :
Gleichung
Zu verwenden
Gleichungen
(ID 3241)
Im Falle einer Waage wirkt auf jeden Arm eine Gravitationskraft, die ein Drehmoment erzeugt
| $ T = r F $ |
Wenn die L ngen der Arme $d_i$ betragen und die Kr fte $F_i$ mit $i=1,2$ sind, verlangt die Gleichgewichtsbedingung, dass die Summe der Drehmomente null ist:
| $\displaystyle\sum_i \vec{T}_i=0$ |
Daher, unter Ber cksichtigung, dass das Vorzeichen jedes Drehmoments von der Richtung abh ngt, in der es eine Rotation induziert,
$d_1F_1-d_2F_2=0$
was zu
| $ d_1 F_1 = d_2 F_2 $ |
f hrt.
(ID 3250)
Si se deriva en el tiempo la relaci n para el momento angular
| $ L = r p $ |
para el caso de que el radio sea constante
$T=\displaystyle\frac{dL}{dt}=r\displaystyle\frac{dp}{dt}=rF$
por lo que
| $ T = r F $ |
(ID 4431)
Beispiele
Wie wir gesehen haben, erf llt das Drehmoment eine analoge Rolle zur Kraft im Falle der Rotation:
$F\longleftrightarrow T$
Um die Bewegungsgleichungen aufzustellen, k nnen wir uns daran erinnern, wie die Kraft in Bezug auf den Impuls definiert wurde:
$F=\displaystyle\frac{\Delta p}{\Delta t}$
und wie das Drehmoment definiert wurde:
$T=\displaystyle\frac{\Delta L}{\Delta t}$
Wir k nnen eine Beziehung zwischen beiden herstellen, um die Erzeugung von Drehmoment aufgrund von Kraft zu beschreiben:
Daher m ssen wir zun chst definieren, was dem Impuls im Kontext der Rotation entspricht.
(ID 325)
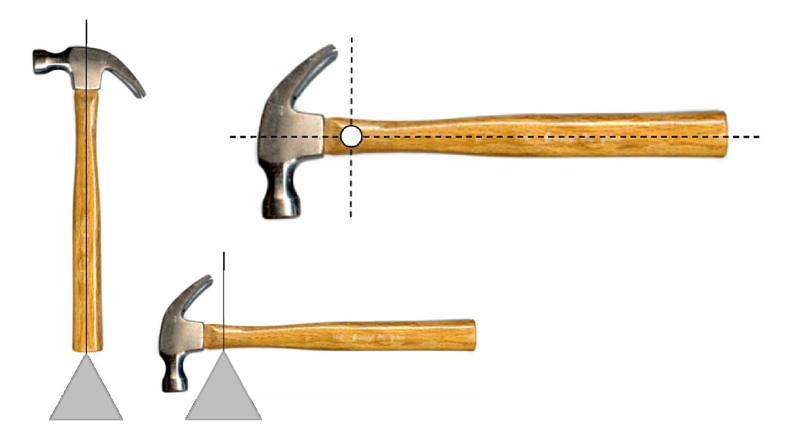
Wenn man die Verteilung der Masse im Raum betrachtet, sollte es immer m glich sein, einen Punkt zu identifizieren, an dem die von der Masse auf einer Seite ausge bte Kraft der auf der anderen Seite erzeugten Kraft entspricht:
Dieses Konzept impliziert, dass f r jede Ausrichtung eines Objekts ein St tzpunkt gefunden werden kann, an dem das Objekt im Gleichgewicht ist. Jeder dieser Punkte entspricht einer vertikalen Linie. Durch Wiederholung dieses Prozesses mit verschiedenen Ausrichtungen des Objekts wird schlie lich deutlich, dass sich die vertikalen Linien an einem bestimmten Punkt im Inneren des Objekts schneiden. Dieser Punkt wird als Schwerpunkt bezeichnet. Im Wesentlichen handelt es sich dabei um den einzigartigen Punkt innerhalb des Objekts, an dem unabh ngig von seiner Ausrichtung immer ein Gleichgewicht erreicht wird.
(ID 323)
Man kann den Schwerpunkt definieren als den Punkt, an dem sich alle vertikalen Linien treffen, die durch Punkte gezogen werden, an denen das System im Gleichgewicht ist:
(ID 11603)
Jeder K rper, der sich sowohl verschiebt als auch dreht, tut dies auf eine Weise, dass:
• seine translatorische Bewegung beschrieben werden kann, als ob die gesamte Masse im Schwerpunkt konzentriert w re,
• seine Rotation um den Schwerpunkt erfolgt, als ob keine Translation stattfinden w rde.
(ID 11604)
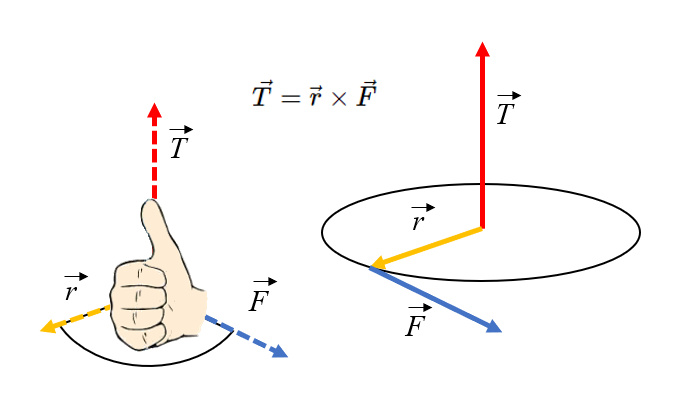
Die Ausrichtung des Drehmoments kann mithilfe der Rechte-Hand-Regel bestimmt werden: Wenn Sie Ihre Finger in Richtung des Radius zeigen lassen und in Richtung der Kraft drehen,
(ID 11602)
ID:(1416, 0)