Energia potencial de um pêndulo matemático para ângulos pequenos
Equação
A energia potencial gravitacional de um pêndulo é
| $ U = m g L (1-\cos \theta )$ |
que pode ser aproximada para ângulos pequenos como:
A energia potencial gravitacional de um pêndulo com massa
| $ U = m g L (1-\cos \theta )$ |
onde
Para ângulos pequenos, a função cosseno pode ser aproximada pela expansão em série de Taylor até a segunda ordem
$\cos\theta\sim 1-\displaystyle\frac{1}{2}\theta^2$
Essa aproximação resulta em uma simplificação da energia potencial para
| $ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$ |
É importante observar que o ângulo deve estar em radianos.
ID:(4514, 0)
Energia cinética rotacional
Equação
No caso em que se estuda a translação, a definição de energia
| $ \Delta W = T \Delta\theta $ |
é aplicada à segunda lei de Newton
| $ T = I \alpha $ |
resultando na expressão
A energia necessária para que um objeto passe da velocidade angular $\omega_1$ para a velocidade angular $\omega_2$ pode ser calculada usando a definição
| $ \Delta W = T \Delta\theta $ |
Com a segunda lei de Newton, podemos reescrever essa expressão como
$\Delta W=I \alpha \Delta\theta=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta$
Usando a definição de velocidade angular
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
obtemos
$\Delta W=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta=I \omega \Delta\omega$
A diferença entre as velocidades angulares é
$\Delta\omega=\omega_2-\omega_1$
Por outro lado, a própria velocidade angular pode ser aproximada pela velocidade angular média
$\omega=\displaystyle\frac{\omega_1+\omega_2}{2}$
Usando ambas as expressões, obtemos a equação
$\Delta W=I \omega \Delta \omega=I(\omega_2-\omega_1)\displaystyle\frac{(\omega_1+\omega_2)}{2}=\displaystyle\frac{I}{2}(\omega_2^2-\omega_1^2)$
Assim, a energia varia de acordo com
$\Delta W=\displaystyle\frac{I}{2}\omega_2^2-\displaystyle\frac{I}{2}\omega_1^2$
Podemos usar isso para definir a energia cinética
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
ID:(3255, 0)
Frequência angular para um pêndulo físico
Equação
No caso do pêndulo físico:
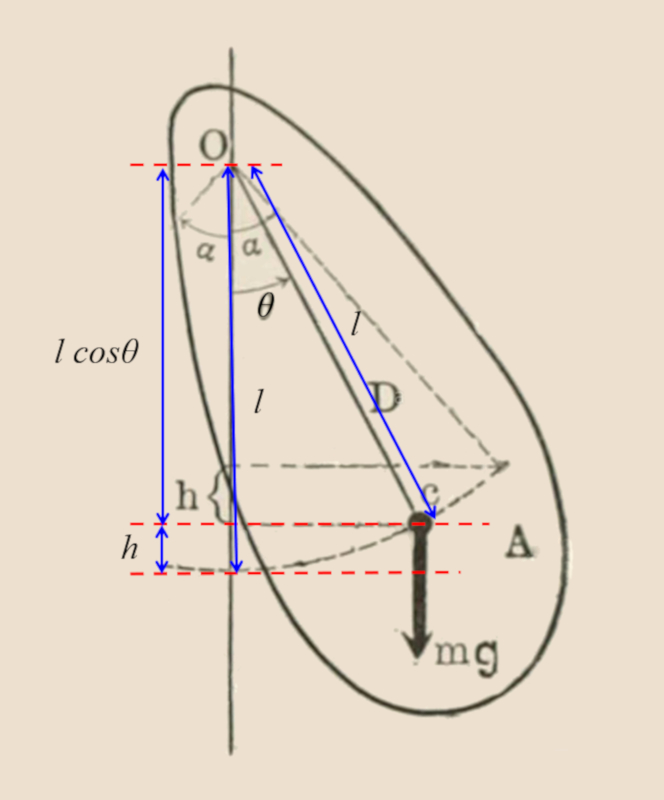
A energia é dada por:
$E=\displaystyle\frac{1}{2}I\omega^2+\displaystyle\frac{1}{2}mgl\theta^2$
Consequentemente, a frequência angular é:
Dado que a energia cinética do pêndulo físico com momento de inércia $I$ e velocidade angular $\omega$ é representada por
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
e a energia potencial gravitacional é dada por
| $ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$ |
onde $m$ é a massa, $l$ é o comprimento da corda, $\theta$ é o ângulo e $g$ é a aceleração angular, a equação de energia pode ser expressa como
$E=\displaystyle\frac{1}{2}I\omega^2+\displaystyle\frac{1}{2}mgl\theta^2$
Como o período é definido como
$T=2\pi\sqrt{\displaystyle\frac{I}{mgl}}$
podemos determinar a frequência angular da seguinte forma:
| $ \omega_0 ^2=\displaystyle\frac{ m g L }{ I }$ |
ID:(4517, 0)
0
Video
Vídeo: Pêndulo Físico
