Utilizador:
Energia cinética rotacional
Equação
No caso em que se estuda a translação, a definição de energia
| $ \Delta W = T \Delta\theta $ |
é aplicada à segunda lei de Newton
| $ T = I \alpha $ |
resultando na expressão
 $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
A energia necessária para que um objeto passe da velocidade angular $\omega_1$ para a velocidade angular $\omega_2$ pode ser calculada usando a definição
| $ \Delta W = T \Delta\theta $ |
Com a segunda lei de Newton, podemos reescrever essa expressão como
$\Delta W=I \alpha \Delta\theta=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta$
Usando a definição de velocidade angular
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
obtemos
$\Delta W=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta=I \omega \Delta\omega$
A diferença entre as velocidades angulares é
$\Delta\omega=\omega_2-\omega_1$
Por outro lado, a própria velocidade angular pode ser aproximada pela velocidade angular média
$\omega=\displaystyle\frac{\omega_1+\omega_2}{2}$
Usando ambas as expressões, obtemos a equação
$\Delta W=I \omega \Delta \omega=I(\omega_2-\omega_1)\displaystyle\frac{(\omega_1+\omega_2)}{2}=\displaystyle\frac{I}{2}(\omega_2^2-\omega_1^2)$
Assim, a energia varia de acordo com
$\Delta W=\displaystyle\frac{I}{2}\omega_2^2-\displaystyle\frac{I}{2}\omega_1^2$
Podemos usar isso para definir a energia cinética
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
ID:(3255, 0)
Energia cinética total com detalhes
Equação
A energia cinética total é calculada somando as energias cinéticas de translação e rotação
| $ K = K_t + K_r $ |
portanto, temos:
| $ K =\displaystyle\frac{1}{2} m v ^2+\displaystyle\frac{1}{2} I \omega ^2$ |
A energia cinética total
| $ K = K_t + K_r $ |
é a soma da energia cinética de translação
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
e a energia cinética de rotação
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
portanto, temos:
| $ K =\displaystyle\frac{1}{2} m v ^2+\displaystyle\frac{1}{2} I \omega ^2$ |
ID:(9944, 0)
Energia cinética de um objeto rolante
Equação
Quando um objeto rola,
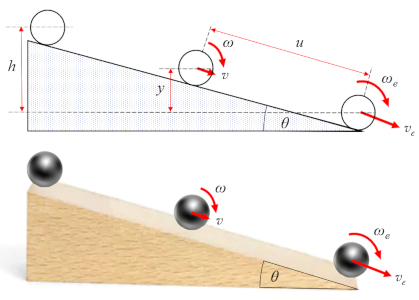
sua velocidade angular está relacionada à velocidade de translação por meio de
| $ v = r \omega $ |
resultando na energia cinética de rotação
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
e, consequentemente, gerando uma energia cinética total
| $ K =\displaystyle\frac{1}{2}\left( m + \displaystyle\frac{ I }{ r ^2}\right) v ^2$ |
Quando um objeto rola, sua velocidade angular está relacionada à velocidade de translação por meio de
| $ v = r \omega $ |
resultando na energia cinética de rotação
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
que se torna
$K_r=\displaystyle\frac{1}{2}I \omega^2=\displaystyle\frac{1}{2} I \displaystyle\frac{v^2}{r^2}=\displaystyle\frac{1}{2}\left(\displaystyle\frac{I}{r^2}\right)v^2$
Assim, combinando a energia cinética de translação
a energia cinética de um corpo que gira é calculada pela soma
| $ K = K_t + K_r $ |
ou seja,
| $ K =\displaystyle\frac{1}{2}\left( m + \displaystyle\frac{ I }{ r ^2}\right) v ^2$ |
ID:(9877, 0)