Storyboard

>Modelo

ID:(752, 0)

Equação

>Top, >Modelo

Na superfície do planeta, a força gravitacional é

e a energia

pode ser demonstrado que neste caso é

$ V = m g z $

Condições

Variáveis

$g$

Aceleração gravitacional

9.8

$m/s^2$

$z$

Altura acima do solo

$m$

$V$

Energia potencial

$J$

$m$

Massa

$kg$

Relação

Desenvolvimento

Como a força gravitacional é

$ F_g = m_g g $

com $m$ representando a massa. Para mover essa massa de uma altura $h_1$ para uma altura $h_2$, é percorrida uma distância de

$ V = m g ( h_2 - h_1 )$

portanto, a energia

$ \Delta W = \vec{F} \cdot \Delta\vec{s} $

com $\Delta s=\Delta h$ nos dá a variação de energia potencial:

$\Delta W = F\Delta s=mg\Delta h=mg(h_2-h_1)=U_2-U_1=\Delta V$

assim, a energia potencial gravitacional é

$ V = m g z $

ID:(3245, 0)

Equação

>Top, >Modelo

Para elevar um objeto da altura $h_1$ para uma altura $h_2$, é necessária energia, que chamaremos de energia potencial gravitacional

e é proporcional à altura ganha:

$ V = m g ( h_2 - h_1 )$

Condições

Variáveis

$g$

Aceleração gravitacional

9.8

$m/s^2$

$h_1$

Altura 1

$m$

$h_2$

Altura 2

$m$

$V$

Energia potencial

$J$

$m$

Massa

$kg$

Relação

Desenvolvimento

Quando um objeto se move de uma altura $h_1$ para uma altura $h_2$, ele percorre a diferença de altura

$h = h_2 - h_1$

assim, a energia potencial

$ V = m g z $

torna-se igual a

$ V = m g ( h_2 - h_1 )$

ID:(7111, 0)

Equação

>Top, >Modelo

Para um pêndulo de comprimento $L$ que é desviado por um ângulo $\theta$, a massa é elevada

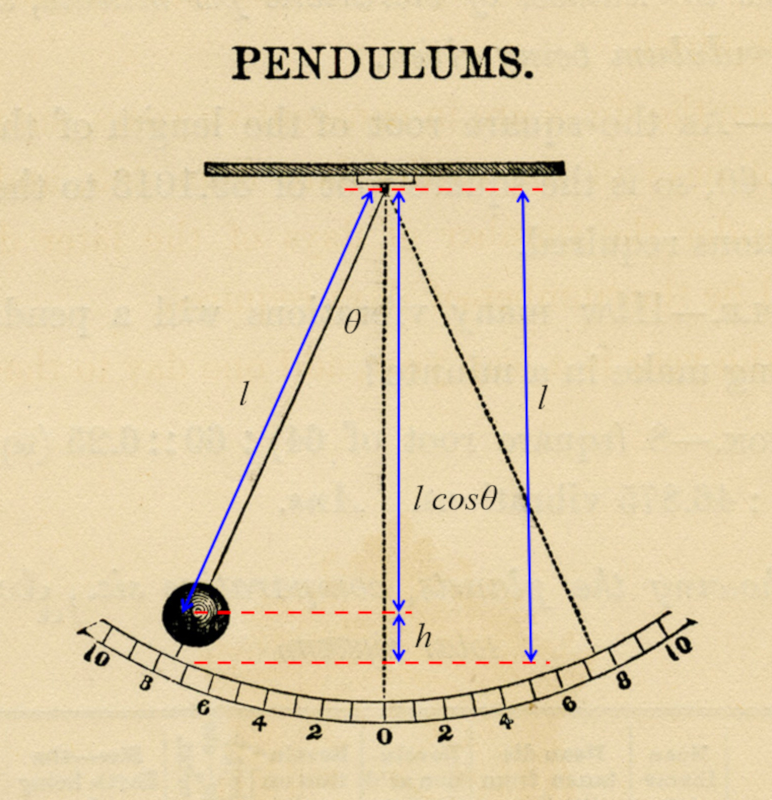
a uma altura igual a:

$ h = L (1-\cos \theta )$

Condições

Variáveis

$h$

Altura no caso do pêndulo

$m$

$\theta$

ângulo de balanço

$rad$

$L$

Comprimento do pêndulo

$m$

Relação

ID:(4523, 0)

Equação

>Top, >Modelo

No caso de uma massa $m$ que pendura em um fio de comprimento $L$ e é desviada por um ângulo $\theta$ em relação à vertical, a massa ganhará uma altura de

portanto, a energia potencial gravitacional

será

$ U = m g L (1-\cos \theta )$

Condições

Variáveis

$g$

Aceleração gravitacional

9.8

$m/s^2$

$\theta$

ângulo de balanço

$rad$

$L$

Comprimento do pêndulo

$m$

$U$

Energia potencial do pêndulo

$J$

$m_g$

Massa gravitacional

$kg$

Relação

onde $g$ é a aceleração devido à gravidade.

ID:(4513, 0)

Equação

>Top, >Modelo

A energia potencial gravitacional de um pêndulo é

que pode ser aproximada para ângulos pequenos como:

$ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$

Condições

Variáveis

$g$

Aceleração gravitacional

9.8

$m/s^2$

$\theta$

ângulo de balanço

$rad$

$L$

Comprimento do pêndulo

$m$

$V$

Energia potencial do pêndulo, para pequenos ângulos

$J$

$m_g$

Massa gravitacional

$kg$

Relação

Desenvolvimento

A energia potencial gravitacional de um pêndulo com massa m, suspenso por um fio de comprimento L e desviado por um ângulo \theta é dada por

$ U = m g L (1-\cos \theta )$

onde g é a aceleração devida à gravidade.

Para ângulos pequenos, a função cosseno pode ser aproximada pela expansão em série de Taylor até a segunda ordem

$\cos\theta\sim 1-\displaystyle\frac{1}{2}\theta^2$

Essa aproximação resulta em uma simplificação da energia potencial para

$ V =\displaystyle\frac{1}{2} m_g g L \theta ^2$

É importante observar que o ângulo deve estar em radianos.

ID:(4514, 0)

Equação

>Top, >Modelo

A elongação $\Delta x$ de uma mola é calculada como a diferença entre a sua posição original $x_1$ e a sua posição atual $x_2$, o que é expresso como

$ V =\displaystyle\frac{1}{2} k ( x_2 ^2- x_1 ^2)$

Condições

Variáveis

$k$

Constante de Hooke

$N/m$

$V$

Energia potencial

$J$

Relação

É comum definir que se uma mola é esticada, a elongação é positiva, e se ela é comprimida, é negativa.

ID:(7112, 0)

Equação

>Top, >Modelo

A força gravitacional em geral é expressa como

enquanto a energia

pode ser mostrado que neste caso é

$ V = - \displaystyle\frac{ G m M }{ r } $

Condições

Variáveis

$G$

Constante gravitacional

6.673e-11

$m^3/kg s^2$

$r$

Distância ao centro do corpo celeste

$m$

$U$

Energia potencial gravitacional geral

$-$

$M$

Massa do corpo celeste

$kg$

$m_g$

Massa gravitacional

$kg$

Relação

Desenvolvimento

Como a força gravitacional é

$ F = G \displaystyle\frac{ m_g M }{ r ^2}$

Para mover uma massa $m$ de uma distância $r_1$ para uma distância $r_2$ a partir do centro do planeta, é necessária uma energia potencial

$ W =\displaystyle\int_C \vec{F} \cdot d \vec{s} $

resultando na energia potencial gravitacional sendo

$W_2-W_1=\displaystyle\int_{r_1}^{r_2}\displaystyle\frac{GmM}{r^2}dr=\displaystyle\frac{GmM}{r_1}-\displaystyle\frac{GmM}{r_2}$

assim obtendo

$ V = - \displaystyle\frac{ G m M }{ r } $

ID:(12551, 0)

0

Video

Vídeo: Energia Potencial