Usuario:
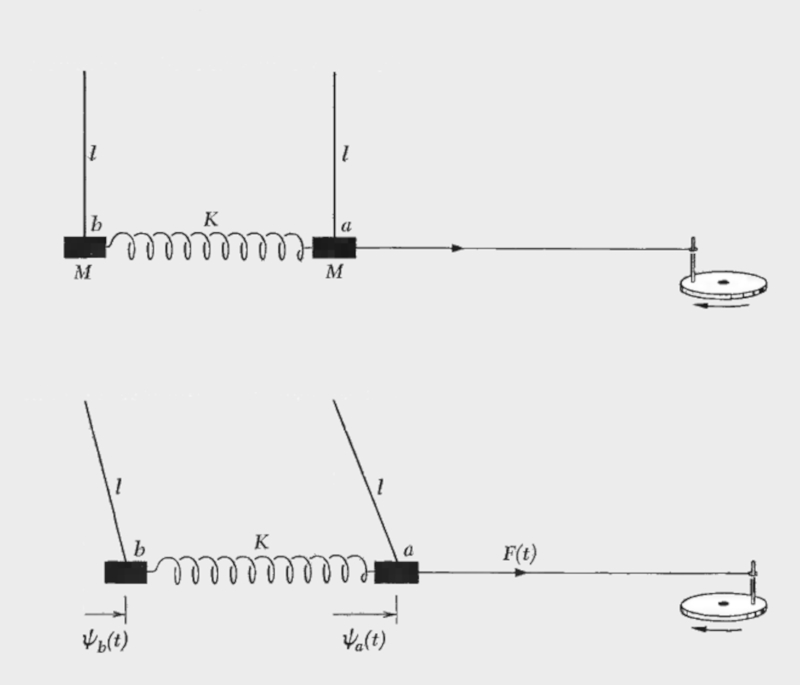
Mecanismo de forzamiento
Ecuación
Para el caso simple la ecuación del oscilador se define por la fuerza según el segundo principio de Newton, la ley de Hook para un resorte y la fuerza externa
$m_ia+ku=F_e \cos(\omega t)$
con
 $\displaystyle\frac{d^2 u }{d t ^2}+\omega_0 ^2 u = f \cos(\omega t)$ |
Con el segundo principio de Newton para masa constante
| $ \bar{F} = m_i a $ |
la ley de Hook de la fuerza que ejerce un resorte
\\n\\ny una fuerza extrena
$m_ia+ku=F_e \cos(\omega t)$
la frecuencia angular del resorte
| $ \omega_0 ^2=\displaystyle\frac{ k }{ m_i }$ |
\\n\\nuna aceleración externa\\n\\n
$f \cos(\omega t) =\displaystyle\frac{F_e}{m_i} \cos(\omega t)$
y la expresión diferencial de la aceleración
| $ a =\displaystyle\frac{ d^2 s }{ d t ^2 }$ |
con lo que
| $\displaystyle\frac{d^2 u }{d t ^2}+\omega_0 ^2 u = f \cos(\omega t)$ |
ID:(12346, 0)
Solución de la ecuación sin amortiguada con forzamiento
Ecuación
Una ecuación de oscilación con forzamiento del tipo
| $\displaystyle\frac{d^2 u }{d t ^2}+\omega_0 ^2 u = f \cos(\omega t)$ |
tiene la forma
| $ u = u_0 \cos( \omega t )$ |
ID:(12571, 0)
Amplitud de la solución sin amortización
Ecuación
Para el caso simple la ecuación del oscilador forzado es del tipo
| $\displaystyle\frac{d^2 u }{d t ^2}+\omega_0 ^2 u = f \cos(\omega t)$ |
Si se asume una solución de la forma
| $ u = u_0 \cos( \omega t )$ |
se tendrá que la amplitud será
| $ u_0 =\displaystyle\frac{ f }{ \omega_0 ^2- \omega ^2}$ |
ID:(12347, 0)
Incluyendo amortiguación
Ecuación
Para el caso simple la ecuación del oscilador se define por la fuerza según el segundo principio de Newton, la fuerza de viscosidad, la ley de Hook para un resorte y la fuerza externa
$m_ia+bv+ku=F_e \cos(\omega t)$
con u la elongación. Con la frecuencia angular propia del resorte, introduciendo una aceleración externa de la fuerza externa y de la masa y expresando la aceleración como la segunda derivada de la elongación (la curvatura) se tiene
| $\displaystyle\frac{d^2 u }{d t ^2}-2\eta \displaystyle\frac{d u }{d t } + \omega_0 ^2 u = f \cos( \omega t )$ |
Con el segundo principio de Newton para masa constante
| $ \bar{F} = m_i a $ |
la fuerza viscosa
| $ F = b v $ |
la ley de Hook de la fuerza que ejerce un resorte
\\n\\ny una fuerza extrena
$m_ia+bv+ku=F_e \cos(\omega t)$
\\n\\nCon un factor de amortiguación\\n\\n
$\eta =\displaystyle\frac{b}{2m_i}$
la frecuencia angular del resorte
| $ \omega_0 ^2=\displaystyle\frac{ k }{ m_i }$ |
\\n\\nuna aceleración externa\\n\\n
$f \cos(\omega t) =\displaystyle\frac{F_e}{m_i} \cos(\omega t)$
y la expresión diferencial de la aceleración
| $ a =\displaystyle\frac{ d^2 s }{ d t ^2 }$ |
con lo que
| $\displaystyle\frac{d^2 u }{d t ^2}-2\eta \displaystyle\frac{d u }{d t } + \omega_0 ^2 u = f \cos( \omega t )$ |
ID:(12403, 0)
Solución de la ecuación amortiguada sin forzamiento
Ecuación
Una ecuación de oscilación amortiguada del tipo
| $\displaystyle\frac{d^2 u }{d t ^2}-2\eta \displaystyle\frac{d u }{d t } + \omega_0 ^2 u = f \cos( \omega t )$ |
asumiendo que no existe formzamiento externo (
| $ u = u_0 e^{- \eta t }\cos(\omega t + \phi )$ |
ID:(12404, 0)
Amplitud de la solución con amortización
Ecuación
Una ecuación de oscilación amortiguada del tipo
| $\displaystyle\frac{d^2 u }{d t ^2}-2\eta \displaystyle\frac{d u }{d t } + \omega_0 ^2 u = f \cos( \omega t )$ |
Si se asume una solución de la forma
| $ u = u_0 e^{- \eta t }\cos(\omega t + \phi )$ |
se tendrá que la amplitud será
| $ u_0 =\displaystyle\frac{ f }{\sqrt{( \omega_0 - \omega )^2+(2 \omega \omega_0 \eta ))^2}}$ |
ID:(12405, 0)
Cambio de fase en la solución amortiguada con forzamiento
Ecuación
Una ecuación de oscilación amortiguada del tipo
| $\displaystyle\frac{d^2 u }{d t ^2}-2\eta \displaystyle\frac{d u }{d t } + \omega_0 ^2 u = f \cos( \omega t )$ |
Si se asume una solución de la forma
| $ u = u_0 e^{- \eta t }\cos(\omega t + \phi )$ |
se tendrá que la amplitud será
| $ \varphi =\arctan\left(\displaystyle\frac{ 2 \omega \omega_0 \eta }{ \omega ^2 - \omega_0 ^2}\right)$ |
ID:(12406, 0)
