Benützer:
Forzamiento
Storyboard 
Variablen
Berechnungen
zu 
,
dann die Variable auswählen: 
zu 
Berechnungen
Variable
Gegeben
Berechnen
Ziel :
Gleichung
Zu verwenden
Gleichungen
Con el segundo principio de Newton para masa constante
la ley de Hook de la fuerza que ejerce un resorte
$m_ia+ku=F_e \cos(\omega t)$
la frecuencia angular del resorte
$f \cos(\omega t) =\displaystyle\frac{F_e}{m_i} \cos(\omega t)$
y la expresi n diferencial de la aceleraci n
con lo que
Con el segundo principio de Newton para masa constante
la fuerza viscosa
la ley de Hook de la fuerza que ejerce un resorte
$m_ia+bv+ku=F_e \cos(\omega t)$
\\n\\nCon un factor de amortiguaci n\\n\\n
$\eta =\displaystyle\frac{b}{2m_i}$
la frecuencia angular del resorte
$f \cos(\omega t) =\displaystyle\frac{F_e}{m_i} \cos(\omega t)$
y la expresi n diferencial de la aceleraci n
con lo que
Beispiele
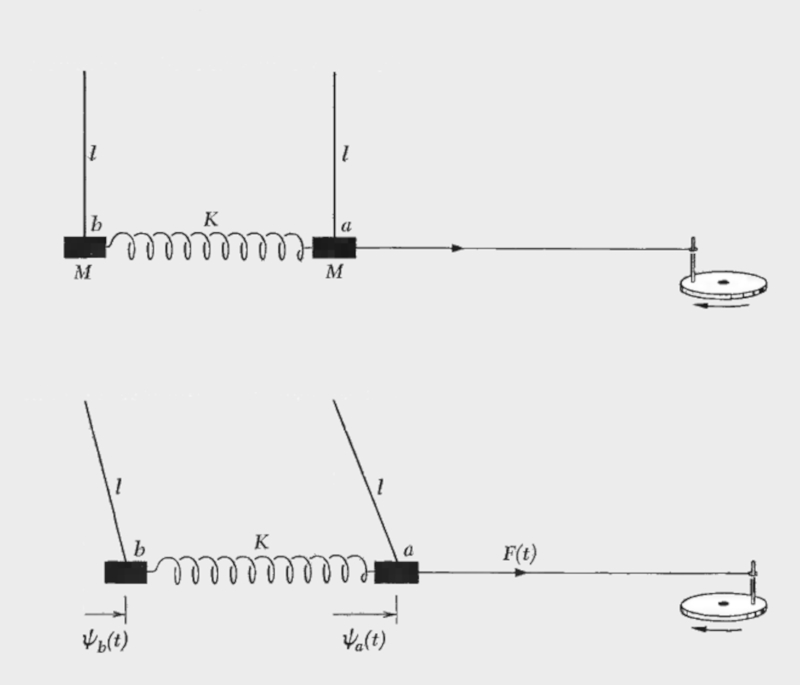
Para el caso simple la ecuaci n del oscilador se define por la fuerza seg n el segundo principio de Newton, la ley de Hook para un resorte y la fuerza externa
$m_ia+ku=F_e \cos(\omega t)$
con
Una ecuaci n de oscilaci n con forzamiento del tipo
tiene la forma
Para el caso simple la ecuaci n del oscilador forzado es del tipo
Si se asume una soluci n de la forma
se tendr que la amplitud ser
Para el caso simple la ecuaci n del oscilador se define por la fuerza seg n el segundo principio de Newton, la fuerza de viscosidad, la ley de Hook para un resorte y la fuerza externa
$m_ia+bv+ku=F_e \cos(\omega t)$
con u la elongaci n. Con la frecuencia angular propia del resorte, introduciendo una aceleraci n externa de la fuerza externa y de la masa y expresando la aceleraci n como la segunda derivada de la elongaci n (la curvatura) se tiene
Una ecuaci n de oscilaci n amortiguada del tipo
asumiendo que no existe formzamiento externo (
Una ecuaci n de oscilaci n amortiguada del tipo
Si se asume una soluci n de la forma
se tendr que la amplitud ser
Una ecuaci n de oscilaci n amortiguada del tipo
Si se asume una soluci n de la forma
se tendr que la amplitud ser
ID:(1643, 0)