A terceira lei da termodin mica afirma que, medida que um sistema se aproxima do zero absoluto, a entropia do sistema se aproxima de um valor m nimo. No zero absoluto, a entropia de uma subst ncia perfeitamente cristalina torna-se zero. Essa lei implica que imposs vel alcan ar o zero absoluto atrav s de um n mero finito de processos. A terceira lei tamb m fornece um ponto de refer ncia para a determina o da entropia, garantindo que os valores de entropia sejam absolutos e n o relativos. Tem implica es significativas para o comportamento dos materiais a temperaturas muito baixas, influenciando fen menos como a supercondutividade e o calor espec fico das subst ncias. Em ess ncia, a terceira lei estabelece uma base para a entropia e destaca a impossibilidade de se atingir o zero absoluto, enfatizando as limita es inerentes aos processos de resfriamento.

mechanisms

A terceira lei da termodin mica [1] estabelece que, medida que a la temperatura absoluta ($T$) de um sistema se aproxima do zero absoluto, a la entropia no limite de temperatura zero ($S$) de uma subst ncia cristalina perfeita se aproxima de um valor m nimo, tipicamente zero. Isso implica que imposs vel alcan ar o zero absoluto atrav s de um n mero finito de processos porque a entropia se tornaria constante. Essencialmente, a terceira lei estabelece que a entropia de um cristal perfeito no zero absoluto zero e destaca a inatingibilidade do zero absoluto devido quantidade infinita de energia necess ria para sua remo o.

equation=10270

Esta lei tem implica es significativas para compreender o comportamento dos materiais a temperaturas muito baixas e fornece um ponto de refer ncia fundamental para calcular os valores de entropia.

[1] " ber die Berechnung chemischer Gleichgewichte aus thermischen Messungen" (Sobre o c lculo dos equil brios qu micos a partir de medi es t rmicas), Walther Nernst, Nachrichten von der Gesellschaft der Wissenschaften zu G ttingen, Mathematisch-Physikalische Klasse, 1906

A rela o de la variação de calor ($\delta Q$) com la temperatura absoluta ($T$) e la variação de entropia ($dS$) pode ser expressa da seguinte forma:

equation=9639

Quando combinamos isso com a rela o entre la calor fornecido ao líquido ou sólido ($\Delta Q$), la calor específico da amostra ($C$) e la variação de temperatura ($\Delta T$):

equation=3197

Obtemos essa rela o no limite infinitesimal, onde:

$\delta Q = C dT = T dS$

Ap s a integra o, chegamos seguinte equa o:

equation=11185

com a condi o de que la entropia básica ($S_0$) seja menor que la temperatura base ($T_0$).

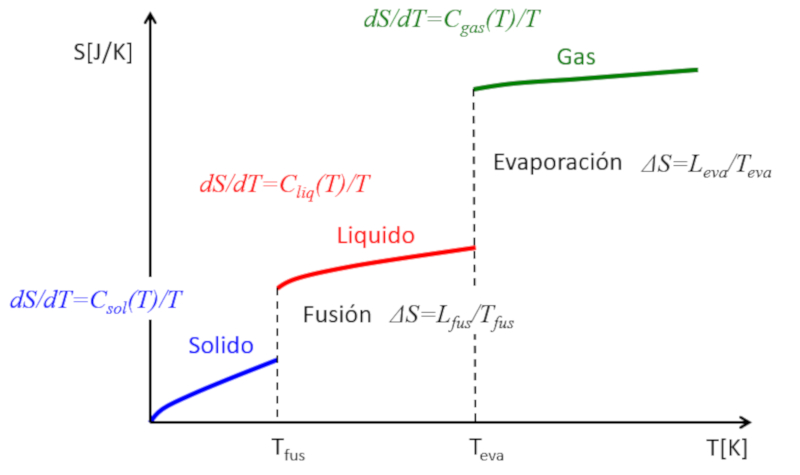
Se a entropia for estimada em fun o da temperatura, as seguintes observa es podem ser feitas:

• Em cada fase (s lido, l quido, gasoso), a entropia tende a aumentar ligeiramente com a temperatura.
• Durante as transi es de fase, ocorre um salto significativo na entropia.

Isso pode ser representado da seguinte forma:

image

Dessa maneira, a entropia pode ser compreendida como uma medida m dia dos graus de liberdade que um sistema possui. Enquanto em cada fase a entropia aumenta gradualmente devido libera o de alguns graus de liberdade adicionais, nas transi es de fase o aumento dram tico. Um s lido composto por m ltiplas liga es que restringem o movimento dos tomos, resultando em poucos graus de liberdade. Em um l quido, muitas liga es s o rompidas, criando novas liberdades que permitem o movimento relativo, levando a m ltiplos novos graus de liberdade. Finalmente, na transi o para a fase gasosa, todas as liga es s o perdidas e cada part cula possui seus tr s graus de liberdade. medida que a temperatura aumenta, as part culas podem rotacionar e oscilar, introduzindo novos graus de liberdade e incrementos adicionais na entropia.

model

A terceira lei da termodin mica estabelece que, quando um sistema levado ao zero absoluto de temperatura, sua entropia se aproxima de zero. Isso pode ser expresso da seguinte forma:

kyon

O diferencial de calor impreciso ($\delta Q$) igual a la temperatura absoluta ($T$) vezes la variação de entropia ($dS$):

kyon

Quando la calor fornecido ao líquido ou sólido ($\Delta Q$) s o adicionados a um corpo, observamos um aumento proporcional de la variação de temperatura ($\Delta T$). Portanto, podemos introduzir uma constante de proporcionalidade la capacidade calórica ($C$), conhecida como capacidade t rmica, que estabelece a seguinte rela o:

kyon

La entropia ($S$) uma fun o de la temperatura absoluta ($T$) com la entropia básica ($S_0$) e la temperatura base ($T_0$) de acordo com:

kyon