A lei de Charles estabelece que o volume de um g s diretamente proporcional sua temperatura quando a press o mantida constante. Isso significa que, medida que a temperatura de um g s aumenta, seu volume tamb m aumenta, desde que a press o permane a a mesma. Inversamente, se a temperatura diminui, o volume tamb m diminui. Essa rela o fundamental para entender o comportamento dos gases e frequentemente observada ao aquecer ou resfriar um g s em um recipiente flex vel, como um bal o, onde a mudan a de temperatura resulta em uma mudan a not vel de volume.

simulation

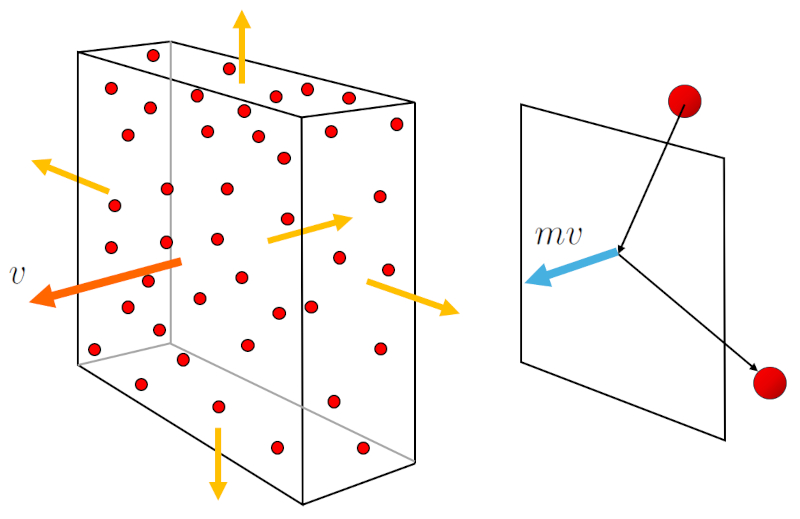
A gera o de la pressão ($p$) ocorre quando as part culas de g s colidem com a superf cie do recipiente de g s. Cada colis o transmite um momento igual ao dobro de la massa molar ($m$) vezes la velocidade média de uma partícula ($\bar{v}$). Al m disso, importante considerar o fluxo de part culas em dire o superf cie, que depende de la concentração de partículas ($c_n$), mas tamb m de la velocidade média de uma partícula ($\bar{v}$), com o qual se deslocam. Portanto,

$p \propto c_n v \cdot m v = c_n m v^2$

O fluxo de part culas e a transmiss o do momento s o representados no seguinte gr fico:

image

Dado que la massa molar ($m$) vezes la velocidade média de uma partícula ($\bar{v}$) ao quadrado proporcional energia, e esta la temperatura absoluta ($T$),

$mv^2 \propto E \propto T$

e, dado que o número de partículas ($N$) constante, la concentração de partículas ($c_n$) inversamente proporcional a o volume ($V$):

$c_n \propto \displaystyle\frac{1}{V}$

Como la pressão ($p$) constante, temos:

$p \propto \displaystyle\frac{T}{V}$

o que implica:

$V \propto T$

A temperatura corresponde energia t rmica (movimento) contida em um objeto.

Uma vez que a energia sempre positiva, escalas de temperatura como Celsius e Fahrenheit, que podem assumir valores negativos, podem parecer n o intuitivas. No entanto, a rela o entre energia e temperatura leva conclus o de que deve existir uma temperatura m nima, conhecida como temperatura zero absoluto, na qual a energia de um sistema de part culas nula.

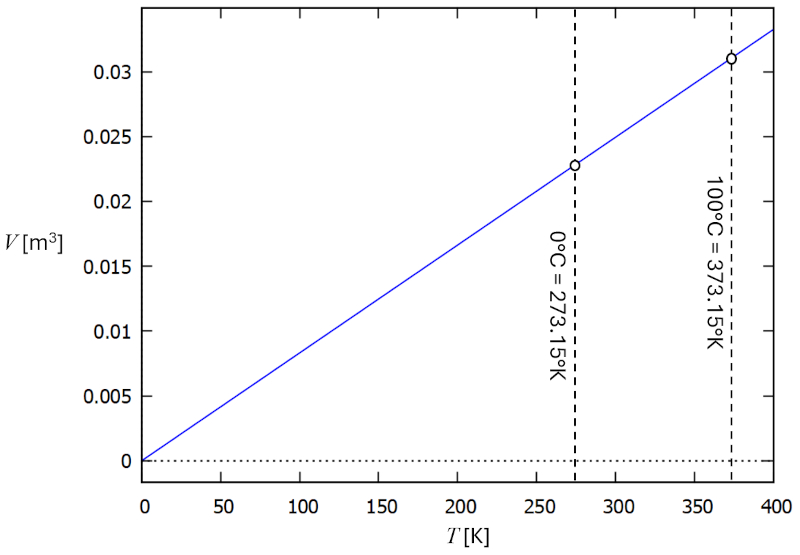
Al m disso, em 1802, Gay-Lussac observou que nos gases existe uma rela o proporcional entre o volume e a temperatura. Essa propor o implica que um g s atingiria um volume de zero a uma temperatura de -273,15 graus Celsius (de acordo com medi es modernas), o que conhecido como temperatura absoluta zero:

image

Isso implica na exist ncia de tal escala, que foi denominada a escala de temperatura absoluta medida em graus Kelvin. Outras escalas, como as temperaturas $t$ em graus Celsius ou Fahrenheit, podem ser convertidas para :

Celsius:

$T = 273.15 + t$

Fahrenheit:

$T = 255.37 + \displaystyle\frac{5}{9} t$

La diferença de temperatura em graus Celsius ($\Delta t$), combinado com la temperatura em graus Celsius no estado 1 ($t_1$) e la temperatura em graus Celsius no estado 2 ($t_2$), resulta em:

$\Delta t = t_2 - t_1$

Se expressarmos ambas as temperaturas em graus Kelvin, temos que la temperatura no estado 1 ($T_1$) igual a:

$T_1 = t_1 + 273.15 , \text{K}$

e la temperatura no estado 2 ($T_2$) igual a:

$T_2 = t_2 + 273.15 , \text{K}$

Portanto, a diferen a de temperaturas em Kelvin, denominada la diferença de temperatura ($\Delta T$), calculada como:

$\Delta T=T_2-T_1=t_2-t_1=\Delta t$

Isso implica:

equation=4380

O que significa que a diferen a entre as temperaturas em graus Celsius e Kelvin permanece a mesma.

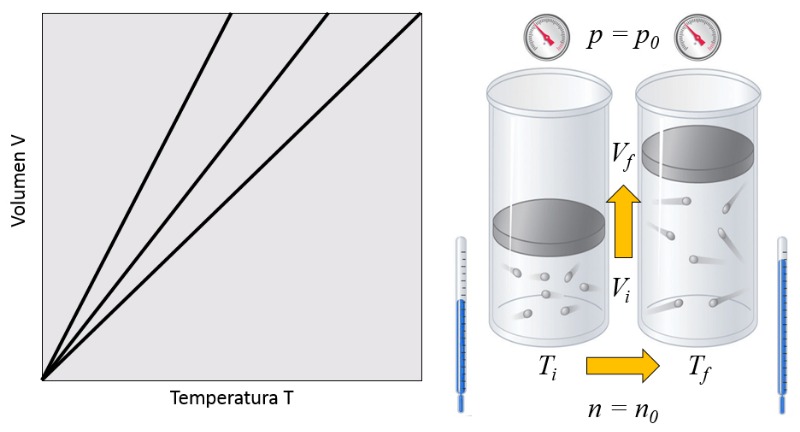
Em um g s, quando la pressão ($p$) e o número de partículas ($N$) s o mantidos constantes, observa-se que o volume ($V$) e la temperatura absoluta ($T$) variam de forma proporcional. Quando o volume ($V$) diminui, la temperatura absoluta ($T$) tamb m diminui, e vice-versa,

$V \propto T$

como mostrado no seguinte gr fico:

image

A lei de Charles [1] afirma que, com la pressão ($p$) e o número de partículas ($N$) constantes, o volume ($V$) e la temperatura absoluta ($T$) s o diretamente proporcionais.

Isso pode ser expresso com la constante da lei de Charles ($C_c$) da seguinte forma:

equation=583

[1] "Sur la dilata o dos gases e vapores" (Sobre a expans o dos gases e vapores), Jacques Charles, Academia Francesa de Ci ncias (1787)

Jacques Charles, nascido em 12 de novembro de 1746 e falecido em 7 de abril de 1823, foi um f sico, inventor e aeronauta franc s. Ele conhecido principalmente por seu trabalho pioneiro no campo da aeron utica e por suas descobertas relacionadas ao comportamento dos gases. Em 1783, realizou o primeiro voo tripulado em um bal o cheio de hidrog nio, em parceria com o qu mico Nicolas-Louis Robert. Esse voo bem-sucedido marcou um marco importante na hist ria da avia o. Charles tamb m fez contribui es importantes para a compreens o das leis dos gases, incluindo a Lei de Charles, que descreve a rela o entre o volume e a temperatura de um g s a press o constante.

Nota: A Lei de Charles foi tornada p blica por Joseph Louis Gay-Lussac, que a atribuiu a Jacques Charles, citando um artigo n o publicado.

image

A lei de Charles estabelece que, com la pressão ($p$) constante, a propor o de o volume ($V$) com la temperatura absoluta ($T$) igual a la constante da lei de Charles ($C_c$):

equation=583

Isso significa que se um g s passa de um estado inicial (o volume no estado i ($V_i$) e la temperatura no estado inicial ($T_i$)) para um estado final (o volume no estado f ($V_f$) e la temperatura no estado final ($T_f$)), mantendo la pressão ($p$) constante, ele deve sempre obedecer lei de Charles:

$\displaystyle\frac{V_i}{T_i} = C_c = \displaystyle\frac{V_f}{T_f}$

Portanto, temos:

equation=3492

Se em um processo isot rmico, no qual o conte do permanece constante, tivermos que la temperatura no estado inicial ($T_i$), la temperatura no estado final ($T_f$), o volume no estado i ($V_i$) e o volume no estado f ($V_f$) est o relacionados pela seguinte equa o:

equation=3492

Ent o, podemos introduzir la densidade ($\rho$), que, juntamente com la massa ($M$) e o volume ($V$), satisfaz:

equation=3704

Isso nos leva a la densidade no estado i ($\rho_i$) e la densidade no estado f ($\rho_f$) como:

equation=8835

model

A lei de Charles estabelece uma rela o entre o volume ($V$) e la temperatura absoluta ($T$), indicando que sua propor o igual a la constante da lei de Charles ($C_c$), da seguinte forma:

kyon

A lei de Charles estabelece uma rela o entre o volume ($V$) e la temperatura absoluta ($T$), indicando que sua propor o igual a la constante da lei de Charles ($C_c$), da seguinte forma:

kyon

Se um g s passa de um estado inicial (i) para um estado final (f) com la pressão ($p$) constante, ent o para o volume no estado i ($V_i$), o volume no estado f ($V_f$), la temperatura no estado inicial ($T_i$) e la temperatura no estado final ($T_f$) v lido:

kyon

La densidade ($\rho$) definido como a rela o entre la massa ($M$) e o volume ($V$), expressa como:

kyon

Essa propriedade espec fica do material em quest o.

La densidade ($\rho$) definido como a rela o entre la massa ($M$) e o volume ($V$), expressa como:

kyon

Essa propriedade espec fica do material em quest o.

Para os estados iniciais (la densidade no estado i ($\rho_i$), o volume no estado i ($V_i$)) e finais (la densidade no estado f ($\rho_f$), o volume no estado f ($V_f$)), a lei de Charles obtida da seguinte forma:

kyon