Kraft eines Frühlings
Storyboard 
Die von einer Feder erzeugte Kraft ist direkt proportional zu ihrer Dehnung.
Die Proportionalitätskonstante wird als Federkonstante oder Hooke-Konstante bezeichnet. Ebenso wird das Verhältnis dieser Kraft als Hooksches Gesetz bezeichnet.
ID:(1414, 0)
Kraft eines Frühlings
Storyboard 
Die von einer Feder erzeugte Kraft ist direkt proportional zu ihrer Dehnung. Die Proportionalitätskonstante wird als Federkonstante oder Hooke-Konstante bezeichnet. Ebenso wird das Verhältnis dieser Kraft als Hooksches Gesetz bezeichnet.
Variablen
Berechnungen
Berechnungen
Gleichungen
Da der Moment ($p$) mit die Träge Masse ($m_i$) und die Geschwindigkeit ($v$) definiert ist,
Wenn die Träge Masse ($m_i$) gleich die Anfangsmasse ($m_0$) ist, k nnen wir den Impuls nach der Zeit ableiten und die Kraft mit konstanter Masse ($F$) erhalten:
$F=\displaystyle\frac{d}{dt}p=m_i\displaystyle\frac{d}{dt}v=m_ia$
Daher kommen wir zu dem Schluss, dass
Da die Kraft mit konstanter Masse ($F$) gleich die Federkraft ($F_k$) minus die Schwerkraft ($F_g$) ist:
Wenn man bedenkt, dass die Kraft mit konstanter Masse ($F$) mit die Träge Masse ($m_i$) und die Augenblickliche Beschleunigung ($a$) ist
und die Federkraft ($F_k$) mit die Hookes Konstante ($k$) und die Verlängerung ($u$) ist
und dass die Schwerkraft ($F_g$) mit die Gravitationsmasse ($m_g$) und die Gravitationsbeschleunigung ($g$) ist
also erhalten wir
Si se cuelga una masa generando una fuerza
a un resorte este ltimo se dilata hasta generar una fuerza que es
que iguala a la fuerza gravitacional que es
Beispiele
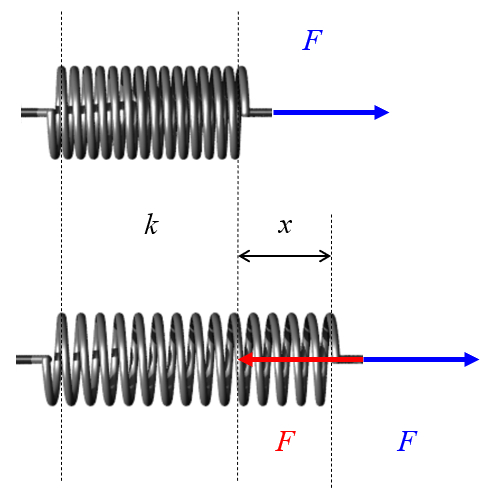
Ein Feder ist ein gewundener Draht, der gedehnt oder komprimiert werden kann.
Bei diesen Verformungen erzeugt die Feder eine Kraft, die sich der Bewegung entgegenstellt.
Wenn die erforderliche Kraft gemessen wird, um eine gegebene Dehnung in der Feder zu erreichen, wird festgestellt, dass sie beide proportional sind:
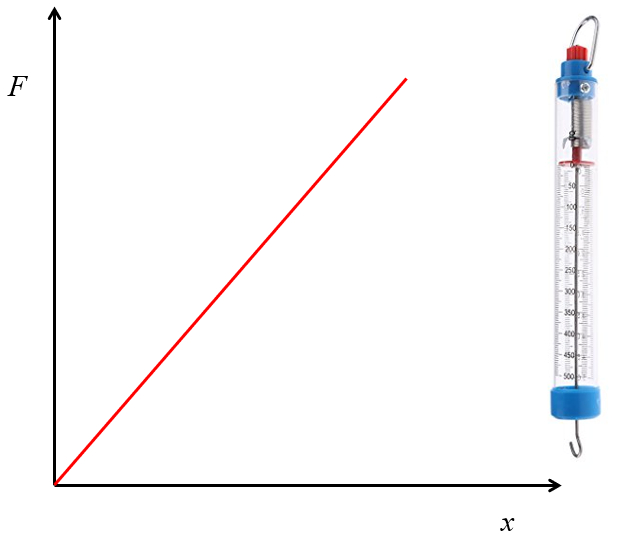
Die Feder wird vertikal aufgeh ngt und bekannte Gewichte werden hinzugef gt. Die resultierende Dehnung wird gemessen und ein Diagramm von Kraft gegen Dehnung wird erstellt. Die Steigung dieser Beziehung, bekannt als Federkonstante oder Hooke'sche Konstante, h ngt von den Eigenschaften der Feder ab.
Die Linearit t dieser Beziehung erm glicht es, Federn als Methode zur Messung von Kr ften zu verwenden.
Kraft kann mithilfe einer Feder gemessen werden, indem eine Skala proportional zur Dehnung erstellt wird, die direkt auf die zugeh rige Kraft hinweist.
Das Instrument zur Messung von Kr ften mithilfe einer Feder wird als Dynamometer bezeichnet (die 'Dina' ist die Einheit der Kraft im cgs-System - Zentimeter, Gramm, Sekunden - so dass 10^5 Dinas einem Newton entsprechen).
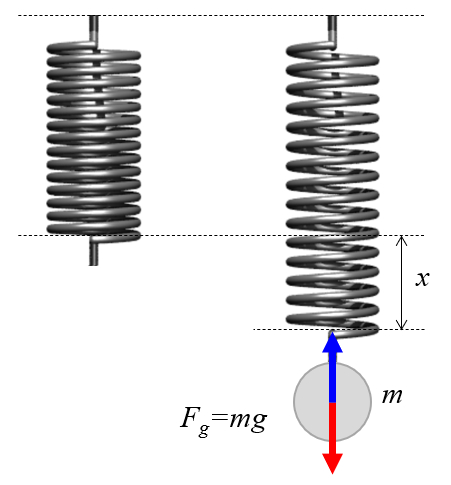
Um zu untersuchen, wie sich die Feder dehnt, kann sie vertikal aufgeh ngt und schrittweise mit bekannten Gewichten belastet werden.
Die Bewegungsgleichung wird durch das Gleichgewicht der Kr fte festgelegt, was bedeutet, dass die Kraft mit konstanter Masse ($F$) gleich die Federkraft ($F_k$) minus die Schwerkraft ($F_g$) ist:
Im Fall, dass die Träge Masse ($m_i$) gleich die Anfangsmasse ($m_0$) ist,
wird die Ableitung des Impulses gleich der Masse mal der Ableitung von die Geschwindigkeit ($v$) sein. Da die Ableitung der Geschwindigkeit die Augenblickliche Beschleunigung ($a$) ist, ergibt sich, dass die Kraft mit konstanter Masse ($F$) ist
Die Beziehung zwischen die Federkraft ($F_k$) und der Dehnung die Verlängerung ($u$) wird als Hooke'sches Gesetz ausgedr ckt und bezeichnet. Die Konstante die Hookes Konstante ($k$) wird als die Federkonstante bezeichnet:
Die Schwerkraft ($F_g$) basiert auf die Gravitationsmasse ($m_g$) des Objekts und auf einer Konstanten, die die Intensit t der Gravitation an der Oberfl che des Planeten widerspiegelt. Letztere wird durch die Gravitationsbeschleunigung ($g$) identifiziert, was $9.8 m/s^2$ entspricht.
Daraus folgt, dass:
Die Bewegungsgleichung wird direkt aus der Kr ftegleichung abgeleitet, wobei die Kraft mit konstanter Masse ($F$) gleich die Federkraft ($F_k$) minus die Schwerkraft ($F_g$) ist:
Diese Gleichung wird in Bezug auf die verschiedenen beteiligten Kr fte ausgedr ckt, einschlie lich die Augenblickliche Beschleunigung ($a$), die Verlängerung der Feder ($x$), die Hookes Konstante ($k$), die Träge Masse ($m_i$), die Gravitationsmasse ($m_g$) und die Gravitationsbeschleunigung ($g$), wie folgt:
Die Massen, die Newton in seinen Prinzipien verwendete, sind mit der Tr gheit der K rper verbunden, was zum Konzept von die Träge Masse ($m_i$) f hrt.
Das nach Newton benannte Gesetz, das die Kraft zwischen K rpern aufgrund ihrer Massen beschreibt, ist mit der Gravitation verbunden und wird daher als die Gravitationsmasse ($m_g$) bezeichnet.
Empirisch wurde festgestellt, dass beide Massen quivalent sind, und daher definieren wir
Einstein war derjenige, der diese Gleichheit in Frage stellte und von diesem Zweifel aus verstand, warum beide in seiner Gravitationstheorie "gleich erscheinen". In seinem Argument erkl rte Einstein, dass Massen den Raum verformen, und diese Raumverformung f hrt zu einer Ver nderung des Verhaltens von K rpern. Auf diese Weise erweisen sich die Massen als quivalent. Das revolution re Konzept der Raumkr mmung impliziert, dass selbst Licht, das keine Masse hat, von Himmelsk rpern beeinflusst wird, was der Gravitationstheorie von Newton widerspricht. Dies wurde experimentell durch die Untersuchung des Verhaltens von Licht w hrend einer Sonnenfinsternis nachgewiesen. In dieser Situation werden Lichtstrahlen aufgrund der Anwesenheit der Sonne abgelenkt, was es erm glicht, Sterne hinter ihr zu beobachten.
Das Produkt von die Hookes Konstante ($k$) und die Träge Masse ($m_i$) wird als die Frecuencia angular del resorte ($\omega$) bezeichnet und wie folgt definiert:
Die Winkelfrequenz ($\omega$) ist mit die Zeit ($T$) gleich
Die Beziehung zwischen die Winkelfrequenz ($\omega$) und die Frequenz des Schalls ($\nu$) wird ausgedrückt als:
Die Frequenz des Schalls ($\nu$) entspricht der Anzahl der Schwingungen, die innerhalb einer Sekunde auftreten. Die Zeit ($T$) repr sentiert die Zeit, die f r eine einzelne Schwingung ben tigt wird. Daher ist die Anzahl der Schwingungen pro Sekunde:
Die Frequenz wird in Hertz (Hz) angegeben.
Die Variable die Schwingungsamplitude ($x$) entwickelt sich in Bezug auf der Zeit ($t$) gem der Bewegungsgleichung mit die Winkelfrequenz des Oszillators ($\omega_0$) und die Gravitationsbeschleunigung ($g$), gegeben durch:
Wenn wir annehmen, dass die Anfangsamplitude der Schwingung ($x_0$) und die Anfangsgeschwindigkeit des Oszillators ($v_0$) die L sung sind, k nnen wir schreiben:
Um die Oszillatorgeschwindigkeit ($v$) zu erhalten, m ssen wir einfach die Schwingungsamplitude ($x$) nach der Zeit ($t$) ableiten:
Daher ergibt sich mit die Anfangsamplitude der Schwingung ($x_0$), die Anfangsgeschwindigkeit ($v_0$) und die Winkelfrequenz des Oszillators ($\omega_0$):
ID:(1414, 0)