Benützer:


Aktion und Reaktion
Storyboard

Newtons drittes Prinzip definiert, dass Kräfte paarweise erzeugt werden müssen, damit ihre Summe Null ist. Dies impliziert, dass vor einer Handlung immer eine Reaktion gleichen Ausmaßes stattfindet, jedoch in die entgegengesetzte Richtung.

>Modell

ID:(755, 0)


Mechanismen
Definition


ID:(15473, 0)


Newtons Dritte Gesetz
Bild

Die Tatsache, dass jede ausgeübte Kraft eine Reaktionskraft erzeugt, ist Teil von Newtons drittem Gesetz:

$ F_R =- F_A $

Eine Konsequenz daraus ist, dass man keine Kraft auf sich selbst ausüben kann, da die Reaktionskraft sie aufhebt. Ein Beispiel hierfür ist die Unmöglichkeit des sogenannten Münchhausen-Effekts. Es wird erzählt, dass der Baron von Münchhausen einmal in einem Sumpf versank. Um sich zu retten, soll der Baron versucht haben, sich an seinen eigenen Haaren hochzuziehen und so aus dem Sumpf zu entkommen.

ID:(10985, 0)


Antreiben
Notiz

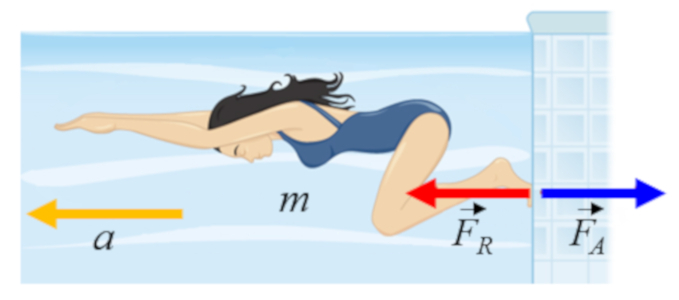
Wenn eine Schwimmerin sich abstößt, wirkt sie eine Kraft von eine Aktion Kraft ($F_A$) auf die Poolwand aus, was wiederum eine Kraft von eine Reaktion Kraft ($F_R$) auf ihren Körper erzeugt und so ihre Bewegung antreibt:

ID:(10976, 0)


Kraft auf eine Wand
Zitat

Wenn wir versuchen, gegen eine Wand zu drücken, werden wir feststellen, dass die Hauptbegrenzung durch die Haftung unserer Schuhe auf dem Boden gegeben ist. Wenn der Boden glatt ist, werden wir typischerweise anfangen zu rutschen, was die von uns ausgeübte Kraft begrenzt.

Es ist interessant zu beachten, dass, wenn wir in einer nicht horizontalen Richtung drücken, die vertikale Komponente unsere vertikale Kraft auf den Boden beeinflusst. Mit anderen Worten führt die vertikale Reaktion auf unsere Aktion gegen die Wand zu einer Zunahme (wenn wir eher nach oben drücken) oder einer Abnahme (wenn wir eher nach unten drücken) unseres Gewichts.

ID:(11533, 0)


Gehen
Übung

Jedes Mal, wenn wir gehen, müssen wir unseren Körper bei jedem Schritt vorantreiben. Dazu setzen wir unseren Fuß auf den Boden, und unter der Annahme, dass er aufgrund der Reibung nicht rutscht, üben unsere Muskeln eine Kraft auf unseren Körper aus, die ihn vorwärts treibt und die Reaktion auf den Fuß überträgt, der sie wiederum auf den Boden (den Planeten) überträgt:

Da der Planet riesig ist, können wir die Auswirkungen dieser Reaktion nicht direkt beobachten. Wenn wir uns jedoch auf einem kleineren Objekt wie einem Zylinder befinden, können wir durch relative Bewegung zur Position auf dem Zylinder dessen Rollbewegung induzieren, während er sich in entgegengesetzter Richtung dreht.

ID:(11532, 0)


Modell
Gleichung


ID:(15475, 0)


Aktion und Reaktion
Beschreibung

Newtons drittes Prinzip definiert, dass Kräfte paarweise erzeugt werden müssen, damit ihre Summe Null ist. Dies impliziert, dass vor einer Handlung immer eine Reaktion gleichen Ausmaßes stattfindet, jedoch in die entgegengesetzte Richtung.

Variablen
Symbol
Text
Variable
Wert
Einheiten
Berechnen
MKS-Wert
MKS-Einheiten
$\Delta t$
Dt
Abgelaufene Zeit
s
$F_A$
F_A
Aktion Kraft
N
$\Delta v_R$
Dv_R
Geschwindigkeitsschwankungen in der Reaktion
m/s
$\Delta p_A$
Dp_A
Impulsvariation in Aktion
kg m/s
$\Delta p_R$
Dp_R
Impulsvariation in der Reaktion
kg m/s
$m_A$
m_A
Masse an Aktion
kg
$m_R$
m_R
Masse an Reaktion
kg
$F_R$
F_R
Reaktion Kraft
N
$\Delta v_A$
Dv_A
Variation der Geschwindigkeit in der Aktion
m/s

Berechnungen

Zuerst die Gleichung auswählen:   zu ,  dann die Variable auswählen:   zu 
Symbol
Gleichung
Gelöst
Übersetzt

Berechnungen

Symbol
Gleichung
Gelöst
Übersetzt

 Variable   Gegeben   Berechnen   Ziel :   Gleichung   Zu verwenden


Gleichungen

Da die Impulsvariation ($\Delta p$) mit die Träge Masse ($m_i$) und die Geschwindigkeit Unterschied ($\Delta v$) gleich ist, haben wir:

$ p = m_i v $



F r den Fall, dass die Masse konstant ist, kann die nderung des Impulses mit der Moment ($p$) und der Anfangsmoment ($p_0$) geschrieben werden, was mit die Geschwindigkeit ($v$) und die Anfangsgeschwindigkeit ($v_0$) kombiniert wird:

$\Delta p = p - p_0 = m_i v - m_i v_0 = m_i ( v - v_0 ) = m_i \Delta v$



wobei die Geschwindigkeit Unterschied ($\Delta v$) berechnet wird durch:

$ dv \equiv v - v_0 $



und somit resultiert:

$ \Delta p = m_i \Delta v $

(ID 13998)

Da die Impulsvariation ($\Delta p$) mit die Träge Masse ($m_i$) und die Geschwindigkeit Unterschied ($\Delta v$) gleich ist, haben wir:

$ p = m_i v $



F r den Fall, dass die Masse konstant ist, kann die nderung des Impulses mit der Moment ($p$) und der Anfangsmoment ($p_0$) geschrieben werden, was mit die Geschwindigkeit ($v$) und die Anfangsgeschwindigkeit ($v_0$) kombiniert wird:

$\Delta p = p - p_0 = m_i v - m_i v_0 = m_i ( v - v_0 ) = m_i \Delta v$



wobei die Geschwindigkeit Unterschied ($\Delta v$) berechnet wird durch:

$ dv \equiv v - v_0 $



und somit resultiert:

$ \Delta p = m_i \Delta v $

(ID 13998)

Beispiele


(ID 15473)

Wenn eine Schwimmerin sich abst t, wirkt sie eine Kraft von eine Aktion Kraft ($F_A$) auf die Poolwand aus, was wiederum eine Kraft von eine Reaktion Kraft ($F_R$) auf ihren K rper erzeugt und so ihre Bewegung antreibt:

(ID 10976)

Wenn wir versuchen, gegen eine Wand zu dr cken, werden wir feststellen, dass die Hauptbegrenzung durch die Haftung unserer Schuhe auf dem Boden gegeben ist. Wenn der Boden glatt ist, werden wir typischerweise anfangen zu rutschen, was die von uns ausge bte Kraft begrenzt.

Es ist interessant zu beachten, dass, wenn wir in einer nicht horizontalen Richtung dr cken, die vertikale Komponente unsere vertikale Kraft auf den Boden beeinflusst. Mit anderen Worten f hrt die vertikale Reaktion auf unsere Aktion gegen die Wand zu einer Zunahme (wenn wir eher nach oben dr cken) oder einer Abnahme (wenn wir eher nach unten dr cken) unseres Gewichts.

(ID 11533)

Jedes Mal, wenn wir gehen, m ssen wir unseren K rper bei jedem Schritt vorantreiben. Dazu setzen wir unseren Fu auf den Boden, und unter der Annahme, dass er aufgrund der Reibung nicht rutscht, ben unsere Muskeln eine Kraft auf unseren K rper aus, die ihn vorw rts treibt und die Reaktion auf den Fu bertr gt, der sie wiederum auf den Boden (den Planeten) bertr gt:

Da der Planet riesig ist, k nnen wir die Auswirkungen dieser Reaktion nicht direkt beobachten. Wenn wir uns jedoch auf einem kleineren Objekt wie einem Zylinder befinden, k nnen wir durch relative Bewegung zur Position auf dem Zylinder dessen Rollbewegung induzieren, w hrend er sich in entgegengesetzter Richtung dreht.

(ID 11532)


(ID 15475)

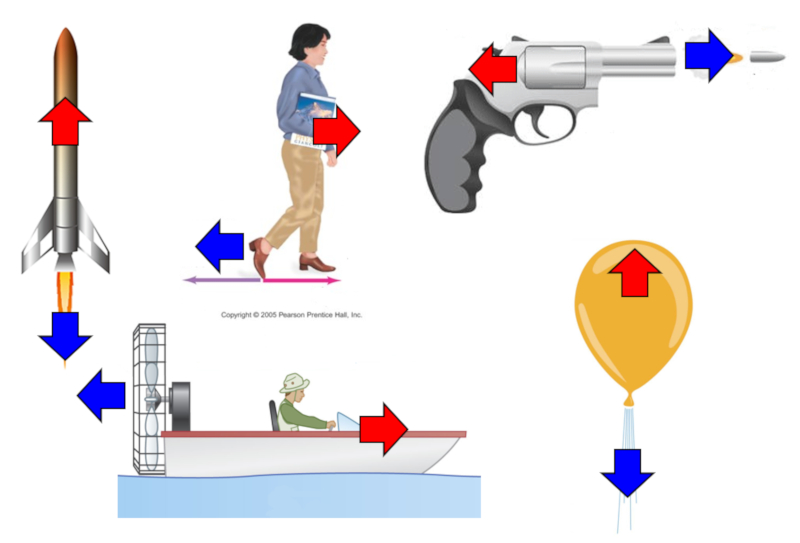
Ein wichtiger Aspekt der Kraft ist, dass sie nicht aus dem Nichts geschaffen werden kann. Jedes Mal, wenn wir versuchen, eine Aktion Kraft ($F_A$) zu erzeugen (eine Aktion), wird zwangsl ufig eine Reaktion Kraft ($F_R$) mit derselben Gr enordnung, aber entgegengesetzter Richtung erzeugt:

$ F_R =- F_A $

Mit anderen Worten: Kr fte entstehen immer paarweise, und die Summe dieser Paare ist immer gleich null.

(ID 10984)

Die Kraft ($F$) wird als die Impulsvariation ($\Delta p$) durch der Abgelaufene Zeit ($\Delta t$) definiert, das durch die Beziehung definiert ist:

$ F \equiv\displaystyle\frac{ \Delta p }{ \Delta t }$

(ID 3684)

Die Kraft ($F$) wird als die Impulsvariation ($\Delta p$) durch der Abgelaufene Zeit ($\Delta t$) definiert, das durch die Beziehung definiert ist:

$ F \equiv\displaystyle\frac{ \Delta p }{ \Delta t }$

(ID 3684)

Falls die Träge Masse ($m_i$) konstant ist, ist die Impulsvariation ($\Delta p$) proportional zu die Geschwindigkeit Unterschied ($\Delta v$):

$ \Delta p = m_i \Delta v $

(ID 13998)

Falls die Träge Masse ($m_i$) konstant ist, ist die Impulsvariation ($\Delta p$) proportional zu die Geschwindigkeit Unterschied ($\Delta v$):

$ \Delta p = m_i \Delta v $

(ID 13998)

ID:(755, 0)