Utilisateur:
Force d'un ressort
Storyboard 
La force générée par un ressort est directement proportionnelle à son allongement.La constante de proportionnalité est appelée la constante du ressort ou constante de Hooke. De même, la relation de cette force est appelée la loi de Hooke.
ID:(1414, 0)
Le ressort
Image
Un ressort est un fil enroulé qui peut être étiré ou comprimé.
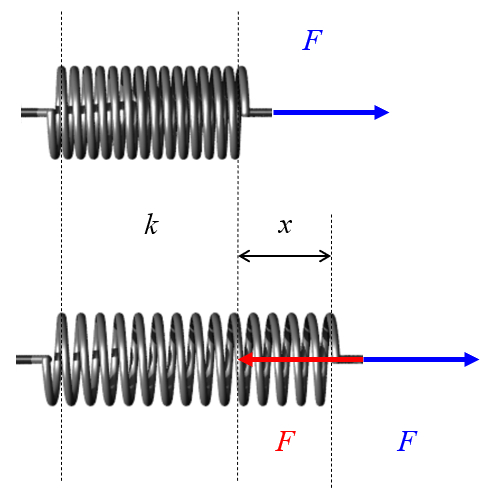
Lorsque ces déformations sont appliquées, le ressort génère une force qui s'oppose au mouvement.
ID:(12527, 0)
Loi de Hooke
Image
Si l'on mesure la force nécessaire pour obtenir une certaine déformation du ressort, on remarquera que les deux grandeurs sont proportionnelles :
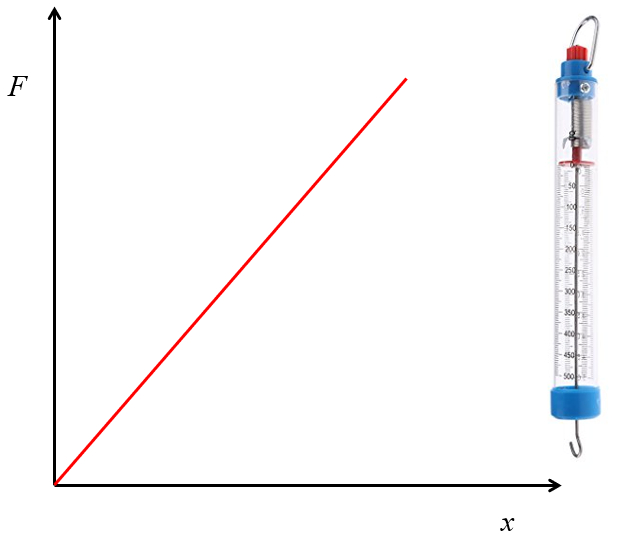
Le ressort est suspendu verticalement et des poids connus sont ajoutés. La déformation résultante est mesurée et un graphique de la force en fonction de la déformation est tracé. La pente de cette relation, appelée constante élastique du ressort ou constante de Hooke, dépend des propriétés du ressort.
La linéarité de cette relation permet d'utiliser les ressorts comme méthode de mesure des forces.
La force peut être mesurée à l'aide d'un ressort, en établissant une échelle proportionnelle à la déformation qui indique directement la force associée.
L'instrument utilisé pour mesurer les forces à l'aide d'un ressort est appelé un dynamomètre (la 'dina' est l'unité de force dans le système cgs - centimètres, grammes, secondes - de telle manière que 10^5 dinas équivalent à un newton).
ID:(11530, 0)
Etude du comportement du ressort
Image
Pour étudier la façon dont le ressort s'allonge, on peut le suspendre verticalement et ajouter progressivement des poids connus.
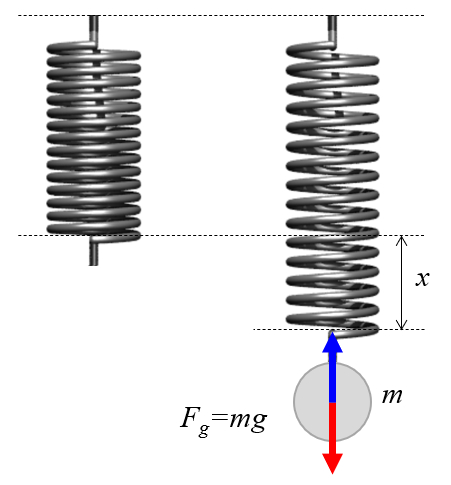
ID:(12528, 0)
Force d'un ressort
Modèle
La force générée par un ressort est directement proportionnelle à son allongement. La constante de proportionnalité est appelée la constante du ressort ou constante de Hooke. De même, la relation de cette force est appelée la loi de Hooke.
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
(ID 3207)
(ID 3241)
tant donn que le moment ($p$) est d fini avec a masse d'inertie ($m_i$) et a vitesse ($v$),
| $ p = m_i v $ |
Si a masse d'inertie ($m_i$) est gal a masse initiale ($m_0$), alors nous pouvons d river la quantit de mouvement par rapport au temps et obtenir a force à masse constante ($F$) :
$F=\displaystyle\frac{d}{dt}p=m_i\displaystyle\frac{d}{dt}v=m_ia$
Par cons quent, nous en concluons que
| $ F = m_i a $ |
(ID 10975)
Comme a force à masse constante ($F$) est gal a force élastique ($F_k$) moins a force gravitationnelle ($F_g$) :
| $ F = F_k - F_g $ |
Si nous consid rons que a force à masse constante ($F$) avec a masse d'inertie ($m_i$) et a accélération instantanée ($a$) est
| $ F = m_i a $ |
et que a force élastique ($F_k$) est avec a constante de Hooke ($k$) et a élongation ($u$)
| $ F_k = k x $ |
et que a force gravitationnelle ($F_g$) est avec a masse gravitationnelle ($m_g$) et a accélération gravitationnelle ($g$)
| $ F_g = m_g g $ |
alors on a
| $ m_i a = k x - m_g g $ |
(ID 11293)
(ID 12338)
(ID 12552)
(ID 15560)
Exemples
(ID 15521)
Un ressort est un fil enroul qui peut tre tir ou comprim .
Lorsque ces d formations sont appliqu es, le ressort g n re une force qui s'oppose au mouvement.
(ID 12527)
Si l'on mesure la force n cessaire pour obtenir une certaine d formation du ressort, on remarquera que les deux grandeurs sont proportionnelles :
Le ressort est suspendu verticalement et des poids connus sont ajout s. La d formation r sultante est mesur e et un graphique de la force en fonction de la d formation est trac . La pente de cette relation, appel e constante lastique du ressort ou constante de Hooke, d pend des propri t s du ressort.
La lin arit de cette relation permet d'utiliser les ressorts comme m thode de mesure des forces.
La force peut tre mesur e l'aide d'un ressort, en tablissant une chelle proportionnelle la d formation qui indique directement la force associ e.
L'instrument utilis pour mesurer les forces l'aide d'un ressort est appel un dynamom tre (la 'dina' est l'unit de force dans le syst me cgs - centim tres, grammes, secondes - de telle mani re que 10^5 dinas quivalent un newton).
(ID 11530)
Pour tudier la fa on dont le ressort s'allonge, on peut le suspendre verticalement et ajouter progressivement des poids connus.
(ID 12528)
(ID 15533)
ID:(1414, 0)