Velocidad Angular
Storyboard 
La variación del angulo en el tiempo se denomina la velocidad angular.
ID:(655, 0)
Velocidad tangencial
Definición 
Si un objeto se somete a un modo de mantener un radio constante, girará como se indica en la figura. Al observar la figura, se notará que la masa realiza un movimiento de traslación con una velocidad tangencial que es igual al radio por la velocidad angular:
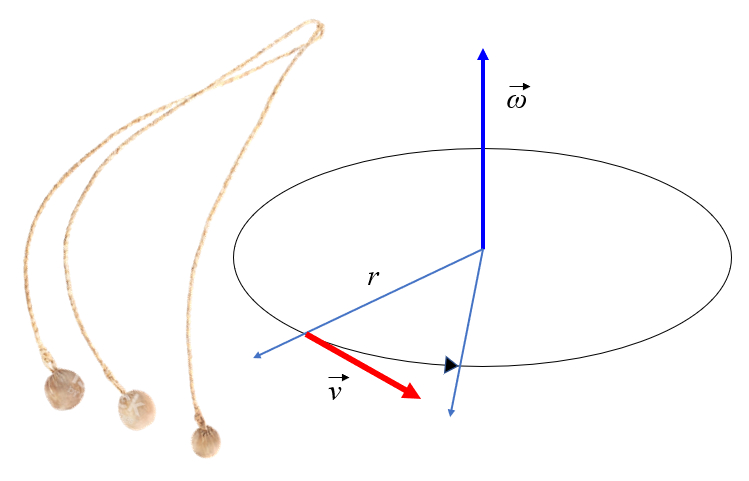
Sin embargo, si se corta el elemento que une el objeto al eje, este continuará moviéndose tangencialmente en línea recta.
ID:(310, 0)
Velocidad Angular
Descripción 
La variación del angulo en el tiempo se denomina la velocidad angular.
Variables
Cálculos
Cálculos
Ecuaciones
En el caso de que la velocidad angular inicial ($\omega_0$) sea igual a la velocidad angular media ($\bar{\omega}$),
| $ \bar{\omega} = \omega_0 $ |
Por lo tanto, con la diferencia de ángulos ($\Delta\theta$), que es igual a el ángulo ($\theta$) dividido por el ángulo inicial ($\theta_0$), obtenemos:
| $ \Delta\theta = \theta_2 - \theta_1 $ |
Y con el tiempo transcurrido ($\Delta t$), que es igual a el tiempo ($t$) dividido por el tiempo inicial ($t_0$), obtenemos:
| $ \Delta t \equiv t - t_0 $ |
Podemos reescribir la ecuaci n de la velocidad angular media ($\bar{\omega}$) como:
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
Esto se puede expresar como:
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
Despejando, obtenemos:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )$ |
(ID 1023)
Si consideramos el ngulo recorrido como la variación del angulo ($\Delta\theta$) en el tiempo $t+\Delta t$ y en $t$:
$\Delta\theta = \theta(t+\Delta t)-\theta(t)$
y usamos el tiempo transcurrido ($\Delta t$), entonces, en el l mite de tiempos infinitesimalmente cortos:
$\omega=\displaystyle\frac{\Delta\theta}{\Delta t}=\displaystyle\frac{\theta(t+\Delta t)-\theta(t)}{\Delta t}\rightarrow lim_{\Delta t\rightarrow 0}\displaystyle\frac{\theta(t+\Delta t)-\theta(t)}{\Delta t}=\displaystyle\frac{d\theta}{dt}$
Esta ltima expresi n corresponde a la derivada de la funci n de ngulo $\theta(t)$, que a su vez es la pendiente de la representaci n gr fica de dicha funci n en el tiempo.
(ID 3232)
La definici n de la velocidad angular media ($\bar{\omega}$) se considera la variación del angulo ($\Delta\theta$),
| $ \Delta\theta = \theta_2 - \theta_1 $ |
y el tiempo transcurrido ($\Delta t$),
| $ \Delta t \equiv t - t_0 $ |
La relaci n entre ambos se define como la velocidad angular media ($\bar{\omega}$):
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
(ID 3679)
(ID 10968)
Ejemplos
Para estimar el desplazamiento de un objeto, es necesario conocer su la velocidad angular ($\omega$) en funci n de el tiempo ($t$). Por lo tanto, se introduce la la velocidad angular media ($\bar{\omega}$), definida como la proporci n entre la variación del angulo ($\Delta\theta$) y el tiempo transcurrido ($\Delta t$).
Para medir esto, se puede utilizar un sistema como el que se muestra en la imagen:
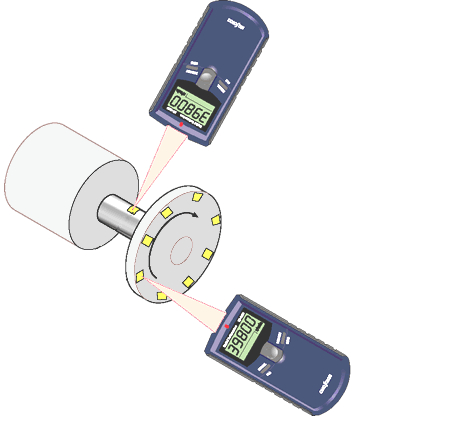
Para determinar la velocidad angular media, se coloca un elemento reflectante en el eje o en un disco con varios elementos reflectantes, y se registra el paso para estimar la longitud del arco $\Delta s$ y el ngulo asociado con el radio $r$. Luego se registra la diferencia de tiempo cuando la marca pasa frente al sensor como $\Delta t$. La velocidad angular media se determina dividiendo el ngulo recorrido por el tiempo transcurrido.
La ecuaci n que describe la velocidad angular media es:
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
Cabe destacar que la velocidad media es una estimaci n de la velocidad angular real. El problema principal es que:
Si la velocidad angular var a durante el tiempo transcurrido, el valor de la velocidad angular media puede ser muy diferente de la velocidad angular promedio.
Por lo tanto, la clave es:
Determinar la velocidad en un tiempo transcurrido suficientemente corto para minimizar su variaci n.
(ID 3679)
La la velocidad angular media ($\bar{\omega}$), calculada a partir de una variación del angulo ($\Delta\theta$) y el tiempo transcurrido ($\Delta t$) mediante la ecuaci n
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
,
es una aproximaci n de la la velocidad angular instantánea ($\omega$) real que tiende a distorsionarse a medida que la velocidad angular fluct a durante el intervalo de tiempo. Por lo tanto, se introduce el concepto de la velocidad angular instantánea ($\omega$) determinada en un tiempo muy peque o. En este caso, hablamos de un intervalo de tiempo infinitesimalmente peque o.
| $ \omega =\displaystyle\frac{ d\theta }{ dt }$ |
que corresponde a la derivada del ngulo.
(ID 3232)
En general, la velocidad angular instantánea ($\omega$) debe entenderse como una entidad tridimensional, es decir, un vector la velocidad angular ($\vec{\omega}$). Cada componente se puede definir como la derivada de el ángulo ($\theta$) respecto a el tiempo ($t$):
| $ \omega =\displaystyle\frac{ d\theta }{ dt }$ |
Por lo tanto, se puede expresar con la derivada en el tiempo ($t$) de el ángulo (vector) ($\vec{\theta}$) como la velocidad angular ($\vec{\omega}$):
| $ \vec{\omega} = \displaystyle\frac{ d\vec{\theta} }{ dt }$ |
(ID 9878)
En el caso de que la velocidad angular sea constante, la velocidad angular media ($\bar{\omega}$) coincide con el valor de la velocidad angular inicial ($\omega_0$), por lo que
| $ \bar{\omega} = \omega_0 $ |
En este caso, podemos calcular el ngulo recorrido en funci n del tiempo recordando que este se asocia a la diferencia entre el ngulo actual y el inicial, as como el tiempo actual y el inicial. Por lo tanto, el ángulo ($\theta$) es igual a el ángulo inicial ($\theta_0$), la velocidad angular inicial ($\omega_0$), el tiempo ($t$) y el tiempo inicial ($t_0$) como se muestra a continuaci n:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )$ |
La ecuaci n representa una recta en el espacio ngulo-tiempo.
(ID 1023)
Si se divide el camino expresado como arco de un circulo se tendr que con es
| $ \Delta s=r \Delta\theta $ |
por el tiempo transcurrido
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
y como la velocidad angular con diferencia de ángulos $rad$, tiempo transcurrido $s$ y velocidad angular media $rad/s$ es
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
se tiene con diferencia de ángulos $rad$, tiempo transcurrido $s$ y velocidad angular media $rad/s$ la relaci n
| $ v_t = r \omega $ |
(ID 10968)
La aceleraci n se define como el cambio en la velocidad angular por unidad de tiempo.
Por lo tanto, la aceleraci n angular la diferencia de velocidades angulares ($\Delta\omega$) se puede expresar en t rminos de la velocidad angular la velocidad angular ($\omega$) y el tiempo la velocidad angular inicial ($\omega_0$) de la siguiente manera:
| $ \Delta\omega = \omega_2 - \omega_1 $ |
(ID 3681)
Si un objeto se somete a un modo de mantener un radio constante, girar como se indica en la figura. Al observar la figura, se notar que la masa realiza un movimiento de traslaci n con una velocidad tangencial que es igual al radio por la velocidad angular:

Sin embargo, si se corta el elemento que une el objeto al eje, este continuar movi ndose tangencialmente en l nea recta.
(ID 310)
ID:(655, 0)
