Aceleración Angular
Storyboard 
La variación de la velocidad angular en el tiempo se denomina la aceleración angular.
ID:(656, 0)
Aceleración de rotación
Definición 
La aceleración angular se define como la variación de la velocidad angular en el tiempo.
ID:(312, 0)
Analogía con la traslación
Imagen 
En analogía al concepto de velocidad, que en traslación corresponde a la variación de la velocidad en el tiempo, se define como la aceleración de la velocidad angular.
ID:(4972, 0)
Diagrama velocidad angular tiempo
Nota 
En el diagrama de velocidad angular vs tiempo la pendiente de la curva corresponde a la aceleración mientras que el área debajo de la curva al angulo acumulado recorrido.
ID:(1024, 0)
Variación de la velocidad angular y duración
Cita 
En un escenario de movimiento de dos cuerpos, el primero modifica su la diferencia de velocidad angular del primer cuerpo ($\Delta\omega_1$) durante la duración del viaje del primer objeto ($\Delta t_1$) con la aceleración angular del primer cuerpo ($\alpha_1$).
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
Posteriormente, el segundo cuerpo avanza, modificando su la diferencia de velocidad angular del segundo cuerpo ($\Delta\omega_2$) durante la duración de viaje del segundo objeto ($\Delta t_2$) con la aceleración angular del segundo cuerpo ($\alpha_2$).
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
Representado gráficamente, obtenemos un diagrama de velocidad y tiempo como se muestra a continuación:
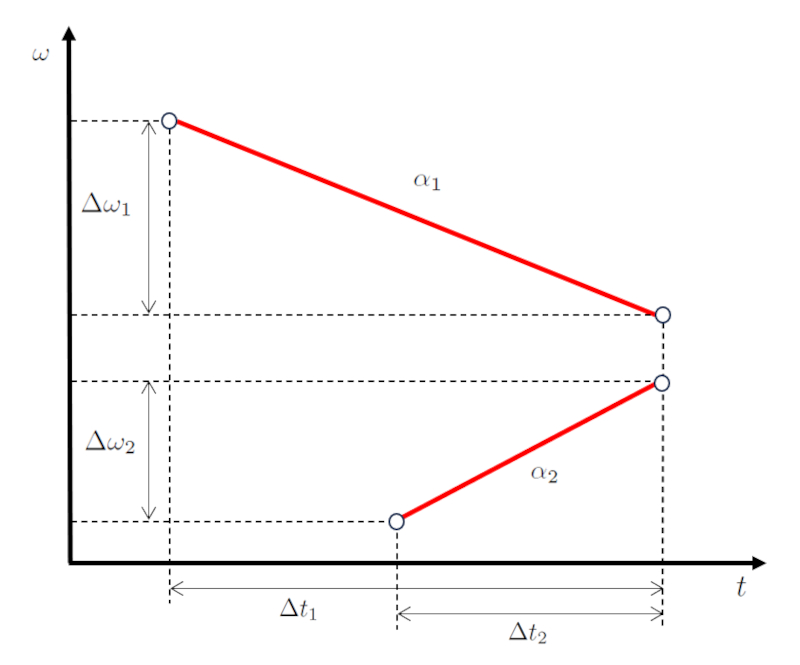
La clave aquí es que los valores la diferencia de velocidad angular del primer cuerpo ($\Delta\omega_1$) y la diferencia de velocidad angular del segundo cuerpo ($\Delta\omega_2$), y los valores la duración del viaje del primer objeto ($\Delta t_1$) y la duración de viaje del segundo objeto ($\Delta t_2$), son tales que ambos cuerpos coinciden en el ángulo y en el tiempo.
ID:(10579, 0)
Aceleración Angular
Descripción 
La variación de la velocidad angular en el tiempo se denomina la aceleración angular.
Variables
Cálculos
Cálculos
Ecuaciones
La aceleraci n angular media se define como la proporci n del ngulo recorrido
| $ \Delta\omega = \omega_2 - \omega_1 $ |
y el tiempo transcurrido
| $ \Delta t \equiv t - t_0 $ |
Esta relaci n entre ambos se establece como la aceleraci n angular media
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
durante dicho intervalo de tiempo.
(ID 3234)
Dado que la aceleración media ($\bar{a}$) es igual a la diferencia de velocidad ($\Delta v$) y el tiempo transcurrido ($\Delta t$) seg n
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
y la aceleración angular media ($\bar{\alpha}$) es igual a la diferencia de velocidades angulares ($\Delta\omega$) y el tiempo transcurrido ($\Delta t$) conforme a
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
se deduce que
$\bar{a}=\displaystyle\frac{\Delta v}{\Delta t}=r\displaystyle\frac{\Delta\omega}{\Delta t}=\bar{\alpha}$
Si asumimos que la aceleración angular media ($\bar{\alpha}$) es igual a la aceleración angular constante ($\alpha_0$)
| $ \bar{\alpha} = \alpha_0 $ |
y suponiendo que la aceleración media ($\bar{a}$) es igual a la aceleración constante ($a_0$)
| $ a_0 = \bar{a} $ |
entonces se obtiene la siguiente ecuaci n:
| $ a = r \alpha $ |
(ID 3236)
Si suponemos que la aceleración angular media ($\bar{\alpha}$) es constante, equivalente a la aceleración angular constante ($\alpha_0$), entonces se aplica la siguiente ecuaci n:
| $ \bar{\alpha} = \alpha_0 $ |
Por lo tanto, al considerar la diferencia de velocidades angulares ($\Delta\omega$) junto con la velocidad angular ($\omega$) y la velocidad angular inicial ($\omega_0$):
| $ \Delta\omega = \omega_2 - \omega_1 $ |
y el tiempo transcurrido ($\Delta t$) en relaci n con el tiempo ($t$) y el tiempo inicial ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
la ecuaci n para la aceleración angular media ($\bar{\alpha}$):
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
puede expresarse como:
$\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}$
Despejando esta ltima, obtenemos:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
(ID 3237)
En el caso de la aceleración angular constante ($\alpha_0$), la velocidad angular ($\omega$) en funci n de el tiempo ($t$) sigue una relaci n lineal con el tiempo inicial ($t_0$) y la velocidad angular inicial ($\omega_0$) de la forma:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
Dado que el ngulo recorrido es igual al rea bajo la curva de velocidad angular-tiempo, en este caso se puede sumar la contribuci n del rect ngulo:
$\omega_0(t-t_0)$
y el tri ngulo:
$\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2$
Esto nos lleva a la expresi n para el ángulo ($\theta$) y el ángulo inicial ($\theta_0$):
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
(ID 3682)
Ejemplos
La aceleraci n angular se define como la variaci n de la velocidad angular en el tiempo.
(ID 312)
En analog a al concepto de velocidad, que en traslaci n corresponde a la variaci n de la velocidad en el tiempo, se define como la aceleraci n de la velocidad angular.
(ID 4972)
La proporci n en la que la variaci n de la velocidad angular a lo largo del tiempo se define como la aceleración angular media ($\bar{\alpha}$). Para medirla, es necesario observar la diferencia de velocidades angulares ($\Delta\omega$) y el tiempo transcurrido ($\Delta t$).
La ecuaci n que describe la aceleración angular media ($\bar{\alpha}$) es la siguiente:
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
(ID 3234)
Al igual que en la aceleraci n de traslaci n, existe el concepto de aceleraci n angular instant nea, que es la aceleraci n angular con aceleración angular media $rad/s^2$, diferencia de velocidades angulares $rad/s$ y tiempo transcurrido $s$
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
que existe en un tiempo espec fico. Esto se calcula en la aproximaci n de intervalos de tiempo muy peque os $(\Delta t\rightarrow 0)$, es decir
$\alpha=\lim_{\Delta t\rightarrow 0}\displaystyle\frac{\Delta\omega}{\Delta t}=\displaystyle\frac{d\omega}{dt}$
donde
| $ \alpha =\displaystyle\frac{ d\omega }{ dt }$ |
(ID 3235)
Con la aceleración angular constante ($\alpha_0$), la velocidad angular ($\omega$) establece una relaci n lineal con el tiempo ($t$), que tambi n incorpora las variables la velocidad angular inicial ($\omega_0$) y el tiempo inicial ($t_0$), tal que:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
Esta ecuaci n representa una recta en el plano de velocidad angular versus tiempo.
(ID 3237)
En el diagrama de velocidad angular vs tiempo la pendiente de la curva corresponde a la aceleraci n mientras que el rea debajo de la curva al angulo acumulado recorrido.
(ID 1024)
Dado que el desplazamiento total corresponde al rea bajo la curva de velocidad angular frente al tiempo, en el caso de una aceleración angular constante ($\alpha_0$), se determina que el desplazamiento el ángulo ($\theta$) con las variables el ángulo inicial ($\theta_0$), el tiempo ($t$), el tiempo inicial ($t_0$) y la velocidad angular inicial ($\omega_0$) es el siguiente:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
Esta expresi n corresponde a la forma general de una par bola.
(ID 3682)
Si dividimos la relaci n entre la velocidad media ($\bar{v}$), el radio ($r$) y la velocidad angular media ($\bar{\omega}$), expresada en la siguiente ecuaci n:
| $ v = r \omega $ |
por el valor de el tiempo transcurrido ($\Delta t$), podemos obtener el factor que nos permite calcular la aceleraci n angular a lo largo de la rbita:
| $ a = r \alpha $ |
(ID 3236)
En un escenario de movimiento de dos cuerpos, el primero modifica su la diferencia de velocidad angular del primer cuerpo ($\Delta\omega_1$) durante la duración del viaje del primer objeto ($\Delta t_1$) con la aceleración angular del primer cuerpo ($\alpha_1$).
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
Posteriormente, el segundo cuerpo avanza, modificando su la diferencia de velocidad angular del segundo cuerpo ($\Delta\omega_2$) durante la duración de viaje del segundo objeto ($\Delta t_2$) con la aceleración angular del segundo cuerpo ($\alpha_2$).
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
Representado gr ficamente, obtenemos un diagrama de velocidad y tiempo como se muestra a continuaci n:

La clave aqu es que los valores la diferencia de velocidad angular del primer cuerpo ($\Delta\omega_1$) y la diferencia de velocidad angular del segundo cuerpo ($\Delta\omega_2$), y los valores la duración del viaje del primer objeto ($\Delta t_1$) y la duración de viaje del segundo objeto ($\Delta t_2$), son tales que ambos cuerpos coinciden en el ngulo y en el tiempo.
(ID 10579)
ID:(656, 0)
