User:
Angle Difference
Equation
To describe the rotation of an object, we need to determine the angle variation ($\Delta\theta$). This is achieved by subtracting the initial Angle ($\theta_0$) from the angle ($\theta$), which is reached by the object during its rotation:
 $ \Delta\theta = \theta - \theta_0 $ |
ID:(3680, 0)
Variation of angular speeds
Equation
Acceleration is defined as the change in angular velocity per unit of time.
Therefore, the angular acceleration the difference in Angular Speeds ($\Delta\omega$) can be expressed in terms of the angular velocity the angular Speed ($\omega$) and time the initial Angular Speed ($\omega_0$) as follows:
| $ \Delta\omega = \omega - \omega_0 $ |
ID:(3681, 0)
Mean angular speed
Equation
To estimate the displacement of an object, it's necessary to know its the angular Speed ($\omega$) as a function of the time ($t$). Therefore, the the mean angular velocity ($\bar{\omega}$) is introduced, defined as the ratio between the angle variation ($\Delta\theta$) and the time elapsed ($\Delta t$).
To measure this, a system like the one shown in the image can be used:
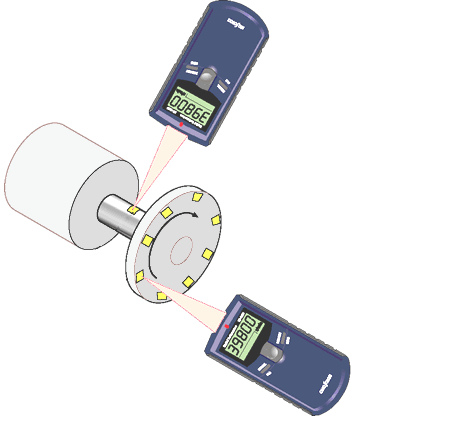
To determine the average angular velocity, a reflective element is placed on the axis or on a disk with several reflective elements, and the passage is recorded to estimate the length of the arc $\Delta s$ and the angle associated with the radius $r$. Then the time difference when the mark passes in front of the sensor is recorded as $\Delta t$. The average angular velocity is determined by dividing the angle traveled by the time elapsed.
The equation that describes the average angular velocity is:
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
The definition of the mean angular velocity ($\bar{\omega}$) is considered as the angle variation ($\Delta\theta$),
| $ \Delta\theta = \theta - \theta_0 $ |
and the time elapsed ($\Delta t$),
| $ \Delta t \equiv t - t_0 $ |
The relationship between both is defined as the mean angular velocity ($\bar{\omega}$):
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
It should be noted that the average velocity is an estimation of the actual angular velocity. The main problem is that:
If the angular velocity varies during the elapsed time, the value of the average angular velocity can be very different from the average angular velocity.
Therefore, the key is:
Determine the velocity in a sufficiently short elapsed time to minimize its variation.
ID:(3679, 0)
Instantaneous Angular Velocity
Equation
The the mean angular velocity ($\bar{\omega}$), calculated from ($$) and the time elapsed ($\Delta t$) using the equation
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
,
is an approximation of the real the instantaneous Angular Speed ($\omega$) that tends to distort as the angular velocity fluctuates over the time interval. Therefore, the concept of the instantaneous Angular Speed ($\omega$) determined at a very small time is introduced. In this case, we are talking about an infinitesimally small time interval.
| $ \omega =\displaystyle\frac{ d\theta }{ dt }$ |
If we consider the angle covered as the angle variation ($\Delta\theta$) at time $t+\Delta t$ and at $t$:
$\Delta\theta = \theta(t+\Delta t)-\theta(t)$
and use the time elapsed ($\Delta t$), then, in the limit of infinitesimally short times:
$\omega=\displaystyle\frac{\Delta\theta}{\Delta t}=\displaystyle\frac{\theta(t+\Delta t)-\theta(t)}{\Delta t}\rightarrow lim_{\Delta t\rightarrow 0}\displaystyle\frac{\theta(t+\Delta t)-\theta(t)}{\Delta t}=\displaystyle\frac{d\theta}{dt}$
This last expression corresponds to the derivative of the angle function $\theta(t)$, which in turn is the slope of the graphical representation of that function over time.
which corresponds to the derivative of the angle.
ID:(3232, 0)
Tangential speed
Equation
Si se divide el camino expresado como arco de un circulo se tendrá que con es
| $ \Delta s=r \Delta\theta $ |
por el tiempo transcurrido
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
y como la velocidad angular con difference of Angles $rad$, mean angular velocity $rad/s$ and time elapsed $s$ es
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
se tiene con difference of Angles $rad$, mean angular velocity $rad/s$ and time elapsed $s$ la relación
| $ v_t = r \omega $ |
ID:(10968, 0)
Angular velocity with constant angular acceleration
Equation
With the constant Angular Acceleration ($\alpha_0$), the angular Speed ($\omega$) forms a linear relationship with the time ($t$), incorporating the variables the initial Angular Speed ($\omega_0$) and the start Time ($t_0$) as follows:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
If we assume that the mean Angular Acceleration ($\bar{\alpha}$) is constant, equivalent to the constant Angular Acceleration ($\alpha_0$), then the following equation applies:
| $ \bar{\alpha} = \alpha_0 $ |
Therefore, considering the difference in Angular Speeds ($\Delta\omega$) along with the angular Speed ($\omega$) and the initial Angular Speed ($\omega_0$):
| $ \Delta\omega = \omega - \omega_0 $ |
and the time elapsed ($\Delta t$) in relation to the time ($t$) and the start Time ($t_0$):
| $ \Delta t \equiv t - t_0 $ |
the equation for the mean Angular Acceleration ($\bar{\alpha}$):
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
can be expressed as:
$\alpha_0 = \alpha = \displaystyle\frac{\Delta \omega}{\Delta t} = \displaystyle\frac{\omega - \omega_0}{t - t_0}$
Solving this, we obtain:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
This equation represents a straight line in the angular velocity versus time plane.
ID:(3237, 0)
Mean Angular Acceleration
Equation
The rate at which angular velocity changes over time is defined as the mean Angular Acceleration ($\bar{\alpha}$). To measure it, we need to observe the difference in Angular Speeds ($\Delta\omega$) and the time elapsed ($\Delta t$).
The equation describing the mean Angular Acceleration ($\bar{\alpha}$) is as follows:
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
The definition of average angular acceleration is based on the angle covered
| $ \Delta\omega = \omega - \omega_0 $ |
and the elapsed time
| $ \Delta t \equiv t - t_0 $ |
The relationship between the two is defined as the average angular acceleration
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
within that time interval.
ID:(3234, 0)
Instantaneous Angular Acceleration
Equation
Similar to translational acceleration, there is the concept of Instantaneous Angular Acceleration, which is the angular acceleration with difference in Angular Speeds $rad/s$, mean Angular Acceleration $rad/s^2$ and time elapsed $s$
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
that exists at a specific time. This is calculated in the approximation of very small time intervals $(\Delta t\rightarrow 0)$, meaning
$\alpha=\lim_{\Delta t\rightarrow 0}\displaystyle\frac{\Delta\omega}{\Delta t}=\displaystyle\frac{d\omega}{dt}$
where
| $ \alpha =\displaystyle\frac{ d\omega }{ dt }$ |
ID:(3235, 0)
Acceleration and Angular Acceleration
Equation
If we divide the relationship between the mean Speed ($\bar{v}$), the radio ($r$), and the mean angular velocity ($\bar{\omega}$), expressed in the following equation:
| $ v = r \omega $ |
by the value of the time elapsed ($\Delta t$), we can obtain the factor that allows us to calculate the angular acceleration along the orbit:
| $ a = r \alpha$ |
Given that the mean Acceleration ($\bar{a}$) equals the speed Diference ($\Delta v$) and the time elapsed ($\Delta t$) according to
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
and the mean Angular Acceleration ($\bar{\alpha}$) equals the difference in Angular Speeds ($\Delta\omega$) and the time elapsed ($\Delta t$) as per
| $ \bar{\alpha} \equiv \displaystyle\frac{ \Delta\omega }{ \Delta t }$ |
it follows that
$\bar{a}=\displaystyle\frac{\Delta v}{\Delta t}=r\displaystyle\frac{\Delta\omega}{\Delta t}=\bar{\alpha}$
Assuming that the mean Angular Acceleration ($\bar{\alpha}$) is equal to the constant Angular Acceleration ($\alpha_0$)
| $ \bar{\alpha} = \alpha_0 $ |
and assuming that the mean Acceleration ($\bar{a}$) equals the constant Acceleration ($a_0$)
| $ a_0 = \bar{a} $ |
then the following equation is obtained:
| $ a = r \alpha$ |
ID:(3236, 0)
Angle at Constant Angular Acceleration
Equation
Given that the total displacement corresponds to the area under the angular velocity versus time curve, in the case of a constant Angular Acceleration ($\alpha_0$), it is determined that the displacement the angle ($\theta$) with the variables the initial Angle ($\theta_0$), the time ($t$), the start Time ($t_0$), and the initial Angular Speed ($\omega_0$) is as follows:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
In the case of the constant Angular Acceleration ($\alpha_0$), the angular Speed ($\omega$) as a function of the time ($t$) follows a linear relationship with the start Time ($t_0$) and the initial Angular Speed ($\omega_0$) in the form of:
| $ \omega = \omega_0 + \alpha_0 ( t - t_0 )$ |
Given that the angular displacement is equal to the area under the angular velocity-time curve, in this case, one can add the contributions of the rectangle:
$\omega_0(t-t_0)$
and the triangle:
$\displaystyle\frac{1}{2}\alpha_0(t-t_0)^2$
This leads us to the expression for the angle ($\theta$) and the initial Angle ($\theta_0$):
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )+\displaystyle\frac{1}{2} \alpha_0 ( t - t_0 )^2$ |
This expression corresponds to the general form of a parabola.
ID:(3682, 0)
Center of mass
Equation
Upon observing an object that is supported from a point, we notice the need to carefully balance it to prevent it from rolling in either direction. This leads us to the concept of finding a point from which the body can be balanced without any rotation.
This point is referred to as the center of mass.
To determine the equilibrium point, we can balance the object along each of its axes. By orienting it in a certain way and finding the position where it remains balanced, we identify an imaginary line upon which the center of mass lies.
Once one of the coordinates of the center of mass has been determined, the object is rotated to find the next coordinate of the center of mass.
In this manner, a point known as the center of mass is determined, and it can be calculated using:
| $ \vec{r}_{CM} =\displaystyle\frac{\displaystyle\sum_i m_i \vec{r}_i }{\displaystyle\sum_i m_i }$ |
If we have multiple masses $m_i$, each one will experience a gravitational force
| $ F_g = m_g g $ |
generating a torque equal to
| $ T = r F $ |
where $r_i$ is the horizontal distance from mass $i$ to the pivot point. The total torque will be
$T=\displaystyle\sum_iT_i$
If $r_{CM}$ is the position of the center of mass, the total torque around this point
$T_{CM}=\displaystyle\sum_i T_i=\displaystyle\sum_i(r_i-r_{CM})m_ig=0$
must be zero. From this equation, we can solve for the center of mass position, resulting in
| $ \vec{r}_{CM} =\displaystyle\frac{\displaystyle\sum_i m_i \vec{r}_i }{\displaystyle\sum_i m_i }$ |
.
.
ID:(3248, 0)
Angular Momentum
Equation
The moment ($p$) was defined as the product of the inertial Mass ($m_i$) and the speed ($v$), which is equal to:
| $ p = m_i v $ |
The analogue of the speed ($v$) in the case of rotation is the instantaneous Angular Speed ($\omega$), therefore, the equivalent of the moment ($p$) should be a the angular Momentum ($L$) of the form:
| $ L = I \omega $ |
.
the inertial Mass ($m_i$) is associated with the inertia in the translation of a body, so the moment of Inertia ($I$) corresponds to the inertia in the rotation of a body.
ID:(3251, 0)
Conservation of Angular Momentum
Equation
Si el momento angular se mantiene constante
| $L=L_0$ |
se tiene con
| $ L = I \omega $ |
se tiene que variaciones en el momento de inercia es compensado con variaciones en la velocidad angular
| $ I_1 \omega_1 = I_2 \omega_2 $ |
ID:(3600, 0)
Centrifugal acceleration based on angular velocity
Equation
If we express the tangential velocity in terms of angular velocity, the centrifugal acceleration is given by:
| $ a_c = r \omega ^2$ |
Since the centrifugal acceleration is equal to
| $ a_c =\displaystyle\frac{ v ^2}{ r }$ |
with
| $ v = r \omega $ |
we can conclude that:
| $ a_c = r \omega ^2$ |
ID:(4384, 0)
Centrifuge acceleration
Concept
If a body fixed to a rope of length $r$ rotates with a tangential velocity $v$, and the rope is cut, the body will continue to move in a straight line with a constant velocity $v$ due to inertia.
Orbit circulates of radio
In a time interval $\Delta t$, the body will have traveled a distance of $v\Delta t$ tangentially to its previous orbit. From the perspective of an observer on the axis of the rotating system, the distance is calculated using the Pythagorean theorem, by adding the square of the orbit radius to the square of the distance traveled:
$\sqrt{r^2+v^2\Delta t^2}$
ID:(1155, 0)
Inertia and Centrifuge Acceleration
Concept
If we study a catapult, we will notice that the projectile initially moves along the curve described by the spoon. This happens because the spoon is designed to hold the projectile. Once the arm stops, the projectile continues in a straight line tangential to the circle it was following.
If an object is not restrained and travels with a tangential velocity $v$, it will cover a distance of $v\Delta t$ in a time interval $\Delta t$, moving from point B to point C. However, if it continues to orbit, after the time interval $\Delta t$, it will reach point D. If the object reaches point C, from the perspective of an observer on Earth, there will be an acceleration that causes the object to move away from Earth (centrifugal acceleration), covering the distance $\Delta r$ in the time interval $\Delta t$.
For an observer in space, an object in orbit is constantly falling: instead of ending up at point C, it falls over the time interval $\Delta t$ covering the distance $\Delta r$ until it reaches point D. In both cases, we can represent the situation graphically, and using the Pythagorean theorem, we can see that the following equation must hold true:
$(r+\Delta r)^2=r^2+(v\Delta t)^2$
Expanding the equation, we get:
$2\Delta rr+\Delta r^2=v^2\Delta t^2$
Since the variation in radius $\Delta r$ is much smaller than the radius itself ($r\ll\Delta r$), we can conclude that:
$2\Delta rr=v^2\Delta t^2$
Solving for $\Delta r$, we find:
$\Delta r=\displaystyle\frac{1}{2}\displaystyle\frac{v^2}{r}\Delta t^2$
Comparing this equation with the equation $s=at^2/2$, we can conclude that the object is accelerating with an acceleration equal to $v^2/r$.
ID:(313, 0)
Centrifugal acceleration
Equation
Bodies tend, by inertia, to move in a straight line at a constant velocity. Therefore, if a body orbits around another, it deviates from its straight path and 'falls' into an orbit. Similarly, if there is nothing to hold a body, it will start moving away from the orbit, experiencing, for an object at the center of the rotating system, an apparent acceleration that moves it away from the center, known as centrifugal acceleration. The acceleration is defined as:
| $ a_c =\displaystyle\frac{ v ^2}{ r }$ |
If the distance traveled is small ($v\Delta t\ll r$), the square root of the distance between the center and the body,
$\sqrt{r^2+(v\Delta t)^2}$
can be approximated as
$r+\displaystyle\frac{1}{2}\displaystyle\frac{v^2}{r}\Delta t^2$
which corresponds to a parabolic relationship with respect to time $\Delta t$. Therefore, the behavior can be described with an acceleration equal to:
| $ a_c =\displaystyle\frac{ v ^2}{ r }$ |
Centrifugal acceleration is an acceleration observed by a system on the axis of rotation when an object moves away (flees) at a constant velocity. For the object moving away, such acceleration does not exist.
ID:(4735, 0)
Centripetal acceleration
Equation
When an object orbits at a radius $r$ with a tangential velocity $v$, it maintains a constant distance from the center equal to the radius.
For an observer external to the system, the body, which would otherwise travel in a straight line due to inertia, deviates from this trajectory while maintaining the distance from the center. From the perspective of this observer, the body is accelerating towards the center (centripetal acceleration) of the orbit. Unlike centrifugal acceleration, the object is experiencing a real acceleration. The magnitude of this acceleration is equal to the centrifugal acceleration but with the opposite sign. Therefore, the magnitude of the centripetal acceleration is:
| $ a_p =\displaystyle\frac{ v ^2}{ r }$ |
Unlike centrifugal acceleration, the centripetal acceleration is measurable for the object that is literally 'falling\' towards the center.
ID:(4383, 0)
Moment of inertia of a particle
Equation
For a particle with mass $m$ orbiting around an axis at a distance equivalent to a radius $r$, the relationship can be established by comparing the angular momentum expressed in terms of the moment of inertia and in terms of the moment, which is equal to:
| $ I = m r ^2$ |
La relación entre momento angular y momento es igual a
| $ L = r p $ |
se puede igualar a
| $ L = I \omega $ |
que tras remplazar
| $ p = m_i v $ |
y
| $ v = r \omega $ |
se puede concluir que la momento de inercia de una partícula girando en una órbita es
| $ I = m r ^2$ |
.
ID:(3602, 0)