Composants du sol
Storyboard 
Les trois composantes principales du sol sont le sable, le limon et l'argile. Alors que les grains de sable et de limon sont relativement sphériques, les particules d'argile ressemblent davantage à de petites plaques ou à des lamelles. De plus, il existe une différence significative de taille entre elles : les grains de sable ne mesurent qu'une fraction de millimètre, les grains de limon ont des dimensions de l'ordre des micromètres, et les particules d'argile sont encore plus petites, ne mesurant que quelques micromètres.
Cette variation de taille des particules a un impact significatif sur la capacité du sol à se compacter. Par exemple, l'argile peut remplir les espaces entre les grains de sable et de limon, ce qui influence les différents degrés de compaction qui peuvent être atteints dans le sol.
ID:(362, 0)
Composants du sol
Storyboard 
Les trois composantes principales du sol sont le sable, le limon et l'argile. Alors que les grains de sable et de limon sont relativement sphériques, les particules d'argile ressemblent davantage à de petites plaques ou à des lamelles. De plus, il existe une différence significative de taille entre elles : les grains de sable ne mesurent qu'une fraction de millimètre, les grains de limon ont des dimensions de l'ordre des micromètres, et les particules d'argile sont encore plus petites, ne mesurant que quelques micromètres. Cette variation de taille des particules a un impact significatif sur la capacité du sol à se compacter. Par exemple, l'argile peut remplir les espaces entre les grains de sable et de limon, ce qui influence les différents degrés de compaction qui peuvent être atteints dans le sol.
Variables
Calculs
Calculs
Équations
Exemples
Lorsque nous observons la surface du sol, nous voyons souvent des pierres ou des rochers, une masse brun tre que nous appelons sol, et quelques plantes.
Cependant, si nous regardons de plus pr s, nous remarquerons que le sol contient des restes de plantes, allant de petites pierres des grains de sable. Ces restes de plantes d compos es constituent de la mati re organique de plus petite taille, parfois se confondant avec le mat riau du sol environnant.
En r sum , nous pouvons identifier :
• Des rochers, des galets et des petits cailloux.
• De la mati re organique pr sente dans le sol.
• Le sol lui-m me.
Dans tous les types de sol, nous trouvons des rochers, des galets et de petits cailloux r partis diff rentes profondeurs. De m me, lorsque le sol en surface s' rode, ces pierres ont tendance rester en surface car le sol environnant a t emport par les coulements d'eau en surface.
La concentration de rochers, de galets et de petits cailloux varie et affecte les propri t s m caniques et hydrodynamiques du sol. D'une part, les roches l'int rieur du sol le stabilisent en lui conf rant une plus grande r sistance la d formation. D'autre part, en raison de leur manque de porosit , elles entravent le flux d'eau, affectant la fois le flux d'eau et le transport de l'humidit par diffusion. cet gard, le r le des roches doit tre pris en compte dans la mod lisation du sol.
l'int rieur des pores du sol de surface se trouve de la mati re organique, qui comprend des r sidus de plantes et d'animaux, de la biomasse microbienne, de l'humus et des substances excr t es par les racines.
Au sein de la biomasse microbienne, nous trouvons des micro-organismes tels que des bact ries et des champignons. L'humus, quant lui, est une mati re organique fortement d compos e d riv e de sources v g tales et microbiennes. Il am liore de mani re significative la capacit du sol retenir les nutriments et l'eau.
Lorsque nous observons une coupe transversale du sol, nous pouvons voir la couverture v g tale en surface, et en dessous, les racines qui p n trent les premiers centim tres du sol, qui contient de la mati re organique. Par mati re organique, nous entendons de la mati re en d composition, des organismes et des micro-organismes qui prosp rent dans des environnements aqueux, c'est pourquoi ils habitent les pores du sol o l'eau est pr sente.
mesure que nous descendons plus profond ment, nous remarquons que la mati re organique diminue progressivement, r v lant le sol sous-jacent, compos de ses trois composantes : sable, limon et argile, ainsi que de roches. La concentration de ces diff rentes composantes varie, cr ant diff rentes couches aux propri t s physiques distinctes et aux capacit s variables d'absorption et de transport de l'eau.
En r sum , dans le sol, nous pouvons identifier des composants autres que la mati re organique et les roches principales :
• Sable
• Limon
• Argile
Le sable fin est un type de particule de sol caract ris par sa petite taille relativement. Il se situe entre les particules de sable plus grossier et les particules de limon plus fines en termes de taille. Les particules de sable fin ont g n ralement une taille variant de 0,02 0,2 millim tres ou de 20 200 microm tres.
Le sable fin est couramment pr sent dans la composition du sol et se caract rise par sa capacit retenir une certaine quantit d'humidit tout en permettant un drainage raisonnable. Il peut contribuer la texture du sol et affecter sa capacit soutenir la croissance des plantes. Les sols avec une proportion plus lev e de sable fin ont tendance avoir de bonnes propri t s d'a ration et de drainage.
La composition chimique du sable peut varier en fonction de son origine et de sa composition min rale. En g n ral, le sable est compos de diff rents min raux, le quartz tant l'un des plus courants. Cependant, la composition chimique exacte du sable peut varier largement. Voici un aper u g n ral de la composition chimique du sable, avec des plages approximatives en pourcentage :
• Quartz ($SiO_2$) 90% - 95% [1]: Le dioxyde de silicium, commun ment appel silice, est le composant principal de la plupart des sables. Il peut constituer entre 60 % et 95 % ou plus de la composition du sable.
• Feldspath ($KAlSi_3O_8 - NaAlSi_3O_8 - CaAl_2Si_2O_8$) <10% [1]: Le feldspath est un autre min ral courant dans le sable, et sa composition peut varier. Le feldspath potassique (K-feldspath), le feldspath sodique (Na-feldspath) et le feldspath calcique (Ca-feldspath) sont diff rents types de min raux de feldspath pr sents dans le sable.
• Mica (Muscovite, Biotite) 1-5% [1]: Les min raux de mica tels que la muscovite et la biotite peuvent varier de 1% 5% ou moins de la composition du limon.
• Autres min raux: Selon la source g ologique du sable, il peut contenir des traces d'autres min raux tels que le feldspath, la mica ou la magn tite.
[1] Tucker, Maurice E. Year 2001. Sedimentary Petrology. Wiley-Blackwell.
Le limon est un type de particule de sol qui se situe entre le sable et l'argile en termes de taille des particules. Les particules de limon ont g n ralement une taille qui varie entre 0,002 et 0,02 millim tres, ce qui quivaut 2 20 microm tres. Ces particules sont plus petites que le sable mais plus grandes que l'argile.
Une caract ristique distinctive du limon est sa capacit retenir l'humidit et les nutriments, ce qui en fait un sol adapt l'agriculture. Cependant, il est important de noter que le limon peut se compacter et pr senter des probl mes de drainage s'il domine dans la composition du sol. Les sols contenant du limon sont souvent fertiles et peuvent soutenir une vari t de cultures lorsqu'ils sont correctement g r s.
La composition chimique du limon peut varier en fonction de son origine et de sa localisation g ographique. Cependant, en termes g n raux, le limon est compos de divers min raux et peut contenir de la mati re organique. Ci-dessous, je fournis une approximation de la composition chimique du limon en termes des principaux l ments, exprim s en pourcentage de la composition totale :
• Quartz ($SiO_2$) 40-60% [1]: Le quartz est souvent le min ral dominant dans le limon, repr sentant g n ralement entre 50% et 70% voire plus de sa composition.
• Feldspath ($KAlSi_3O_8 - NaAlSi_3O_8 - CaAl_2Si_2O_8$) <10% [1]: Les min raux de feldspath, comprenant le feldspath potassique, le feldspath sodique et le feldspath calcique, peuvent varier de 10% 30% voire plus de la composition.
• Mica (Muscovite, Biotite) < 5% [1]: Les min raux de mica tels que la muscovite et la biotite peuvent varier de 1% 5% ou moins de la composition du limon.
• Autres Min raux: Le limon peut contenir des traces de divers autres min raux en fonction de son origine g ologique sp cifique, tels que le zircon, la grenat et d'autres.
[1] Tucker, Maurice E. Year 2001. Sedimentary Petrology. Wiley-Blackwell.
L'argile est un type de particule du sol caract ris e par des particules tr s fines, g n ralement plus petites que 0,002 millim tres de taille ou moins de 2 microm tres. Les particules d'argile sont beaucoup plus petites que celles du sable et du limon. Les sols argileux sont connus pour leur capacit retenir l'eau et les nutriments en raison de leur petite taille de particule et de leur grande surface sp cifique. Cependant, ils peuvent aussi se compacter facilement et pr senter des propri t s de drainage d ficientes. Les sols argileux peuvent varier en couleur et en texture en fonction de leur composition min rale et de leur teneur en mati re organique. Ils sont un composant important de nombreux types de sols et peuvent influencer la fertilit et la structure du sol.
La composition chimique de l'argile peut varier en fonction de sa composition min rale sp cifique et de son origine. L'argile est principalement compos e de particules min rales tr s fines et comprend g n ralement plusieurs min raux, notamment :
• Kaolinite ($Al_2Si_2O_5(OH)_4$) 20-40% [1]: La kaolinite est un min ral d'argile courant et le composant principal de l'argile de kaolin.
• Illite ($(K, H_3O)(Al, Mg, Fe)_2(Si, Al)_4O{10}[(OH)_2,(H_2O)]$) 10-40% [1]: L'illite est un autre min ral d'argile courant.
• Smectites/Montmorillonite ($(Na, Ca)_{0.33}(Al, Mg)_2(Si_4O_{10})(OH)_2 n(H_2O)$) 10-40% [1]: La montmorillonite est un min ral d'argile connu pour ses propri t s d'expansion.
• Chlorite ($(Mg, Fe)_3(Si, Al)_4O_{10}(OH)_2 (Mg, Fe)_3(OH)_6$) <10% [1]: Parfois, la chlorite est pr sente dans les min raux d'argile.
• Autres Min raux: En outre, en fonction du d p t sp cifique d'argile, d'autres min raux peuvent galement tre pr sents en quantit s minimes, notamment du quartz, du feldspath et divers oxydes m talliques.
[1] Clay Mineralogy, Ralph E. Grim, McGraw-Hill International Series
Pour mod liser efficacement le sol, il est essentiel de prendre en compte les formes g om triques qui d crivent le mieux les diff rents types de grains qui composent le sol.
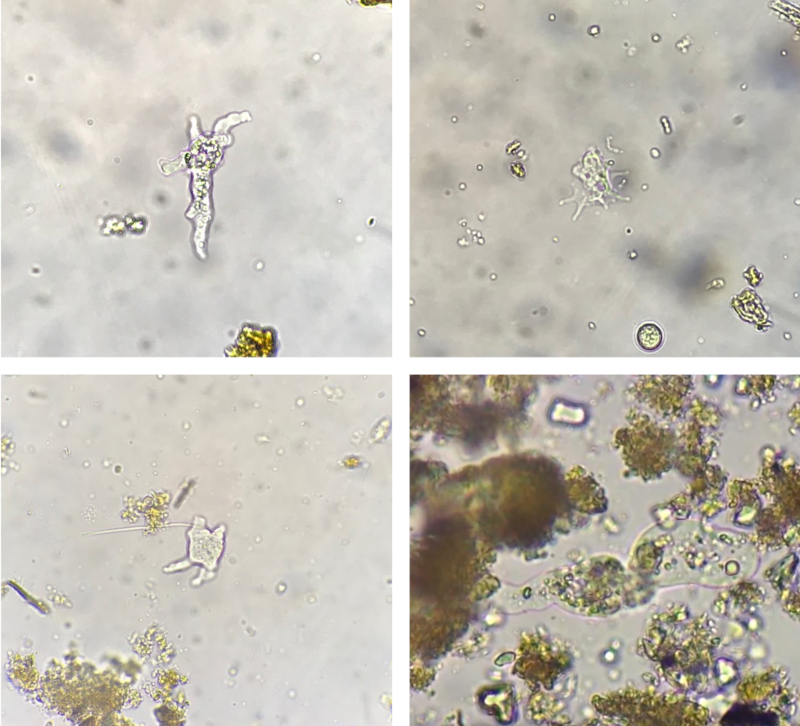
Cela implique d'observer plusieurs grains de chaque type. Dans le cas du sable, cela peut tre r alis l'aide d'un microscope ordinaire, ce qui nous permet de rassembler des collections de grains, comme le montre l'image ci-dessous :
Dans ce cas, nous pouvons conclure que la forme est arrondie, ce qui nous permet de les repr senter efficacement sous forme de sph res.
En g n ral, les grains de sable et les grains de limon sont des conglom rats de cristaux multiples expos s des impacts lors de leur transport par l'eau ou le vent. Ces impacts cr ent des fractures le long des plans cristallins, enlevant les fragments saillants et, par cons quent, arrondissant le grain :
De cette mani re, ils ont tendance devenir plus arrondis et acqu rir une forme qui ressemble de petites sph res.
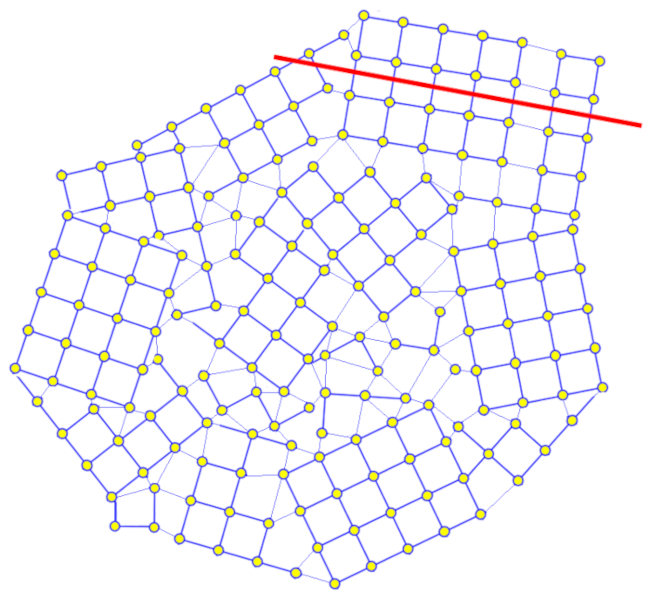
Les grains d'argile sont g n ralement de petits cristaux expos s des chocs lors de leur transport par l'eau ou le vent. Ces chocs g n rent des fractures le long des plans cristallins, ce qui, tant donn que le grain est un cristal, implique qu'il conserve sa forme sans arrondir les coins :
Par cons quent, les grains d'argile se caract risent par une forme g om trique similaire de petites plaques ressemblant des parall l pip des droits.
Si nous observons les grains sous un microscope, nous remarquerons qu'ils ont des formes relativement arrondies et des tailles variables, bien qu'ils aient tendance avoir une taille similaire:
Par cons quent, dans une premi re approximation, les grains peuvent tre mod lis s comme des sph res :
Les grains de sable peuvent tre mod lis s comme des sph res. Pour simplifier le mod le, on suppose qu'ils sont tous identiques. Cependant, un mod le plus d taill pourrait tenir compte de la distribution de diff rents rayons.
Conform ment l'hypoth se initiale selon laquelle les grains de sable peuvent tre mod lis s comme des sph res, leur rayon correspondant peut tre introduit.
Par cons quent, nous introduisons le rayon le rayon du grain de sable ($r_a$) pour d crire les sph res des grains de sable.
Il convient de noter que le rayon est une valeur moyenne, car il varie entre les diff rents grains.
Si nous observons les grains de limon sous un microscope, nous remarquerons qu'ils ont des formes relativement cubiques et des tailles variables, bien qu'ils aient tendance avoir une taille similaire :
Par cons quent, en premi re approximation, les grains peuvent tre mod lis s comme des cubes :
Les grains de limon peuvent tre mod lis s comme des cubes. Pour simplifier le mod le, on suppose qu'ils ont tous la m me taille. Cependant, un mod le plus d taill pourrait prendre en compte la distribution de diff rentes longueurs de c t .
En accord avec l'hypoth se initiale selon laquelle les grains de limon peuvent tre mod lis s comme des cubes, leur longueur de c t correspondante peut tre introduite.
Par cons quent, nous introduisons le c t du cube le côté grain de limon ($a_i$) pour d crire les grains de limon.
Il convient de noter que la longueur du c t est une valeur moyenne, car elle varie d'un grain l'autre.
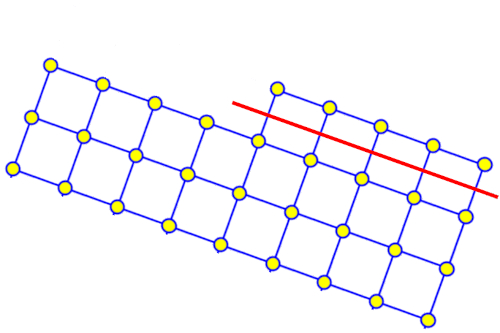
Les grains d'argile sont relativement plats et ont tendance s'empiler de mani re parall le, comme on peut le voir sur cette image obtenue gr ce un microscope lectronique :
Leur forme ressemble des l ments plats d' paisseur r duite qui ressemblent des parall l pip des rectangles :
Les grains d'argile peuvent tre mod lis s comme des parall l pip des rectangles. Pour simplifier le mod le, on suppose qu'ils sont tous identiques. Cependant, un mod le plus d taill pourrait tenir compte de la distribution de diff rentes longueurs et hauteurs.
Conform ment l'hypoth se initiale selon laquelle les grains d'argile peuvent tre mod lis s comme des parall l pip des rectangles, leurs longueurs et hauteurs correspondantes peuvent tre introduites.
Par cons quent, il est introduit pour d crire le parall l pip de droit le longueur et largeur d'une plaque d'argile ($l_c$) et a hauteur d'une plaque d'argile ($w_c$).
Il convient de noter que les longueurs et la hauteur sont des valeurs moyennes, car elles varient r ellement entre les diff rents grains.
Pour calculer la masse d'un grain de sable, il est essentiel de conna tre sa densit . Cependant, il est important de noter que la densit du grain individuel diff re consid rablement de la densit globale du sable en raison de sa haute porosit . Par cons quent, pour estimer la densit d'un grain de sable, il est n cessaire d'examiner la densit de ses min raux principaux, comme d taill ci-dessous :
| Min ral | Occurrence | Densit [$g/cm^3$] |
| Quartz | 90-95% [1] | 2.65 [2] |
| Feldspaths | <10% [1] | 2.50-2.80 [2] |
| Micas | <5% [1] | 2.70-3.30 [2] |
[1] Sedimentary Petrology, Tucker, Maurice E. (2001). Wiley-Blackwell.
[2] Manual of Mineralogy (22nd ed.), Klein, C., & Hurlbut, C. S. Jr. (1993). John Wiley & Sons.
Pour d velopper un mod le simple, nous pouvons supposer une densit homog ne :
Si nous supposons que les min raux composant les grains de sable sont r partis de mani re homog ne, nous pouvons en d duire que les grains ont une densit constante et uniforme en tous points.
Cela introduit a densité d'un grain de sable ($\rho_a$).
Il est important de garder l'esprit que cette valeur peut varier en fonction de la composition sp cifique des grains de sable.
Pour calculer la masse d'un grain de limon, il est essentiel de conna tre sa densit . Cependant, il est important de souligner que la densit du grain individuel diff re consid rablement de la densit du limon dans son ensemble en raison de la pr sence d'une forte porosit dans ce dernier. Par cons quent, pour estimer la densit d'un grain de limon, il est n cessaire d'analyser la densit de ses principaux min raux, qui sont d taill s ci-dessous:
| Min ral | Occurrence | Densit [$g/cm^3$] |
| Quartz | 40-60% [1] | 2.65 [2] |
| Feldspaths | <10% [1] | 2.50-2.80 [2] |
| Micas | <5% [1] | 2.70-3.30 [2] |
[1] Sedimentary Petrology, Tucker, Maurice E. (2001). Wiley-Blackwell.
[2] Manual of Mineralogy (22nd ed.), Klein, C., & Hurlbut, C. S. Jr. (1993). John Wiley & Sons.
Pour d velopper un mod le simple, nous pouvons supposer une densit homog ne :
Si nous supposons que les min raux composant les grains de limon sont r partis de mani re homog ne, nous pouvons en d duire que les grains ont une densit constante et uniforme en tous points.
Cela introduit a densité d'un grain de limon ($\rho_i$).
Il est important de garder l'esprit que cette valeur peut varier en fonction de la composition des grains de limon.
Pour calculer la masse d'un grain d'argile, il est essentiel de conna tre sa densit . Cependant, il est crucial de noter que la densit du grain individuel diff re significativement de la densit de l'argile dans son ensemble en raison de la pr sence notable d'une forte porosit dans cette derni re. Par cons quent, pour estimer la densit d'un grain d'argile, il est n cessaire d'analyser la densit de ses min raux principaux, qui sont d taill s ci-dessous :
| Min ral | Occurrence | Densit [$g/cm^3$] |
| Smectites | 0-80% [1] | 2.75-2.78 [2] |
| Illites | 10-80% [1] | 2.60-2.86 [2] |
| Kaolinites | 20-80% [1] | 2.62-2.66 [2] |
| Chlorites | 0-30% [1] | 2.60-2.96 [2] |
[1] Clay Mineralogy, Ralph E. Grim (1968), McGraw-Hill
[2] Geotechnical Engineering Principles and Practices, Donald P. Coduto et al. (1998), Prentice-Hall
Pour d velopper un mod le simple, nous pouvons supposer une densit homog ne :
Si nous supposons que les min raux composant les grains d'argile sont r partis de mani re homog ne, nous pouvons en d duire que les grains ont une densit constante et uniforme en tous points.
Cela introduit a longueur et largeur d'une plaque d'argile ($\rho_c$).
Il est important de garder l'esprit que cette valeur peut varier en fonction de la composition sp cifique des grains d'argile.
L' tude des grains dans un chantillon de sol implique une analyse approfondie de divers aspects qui contribuent la compr hension des propri t s physiques et du comportement du sol. Voici une explication d taill e des principaux composants de cette tude:
Termes de Taille:
- Les termes de taille font r f rence la cat gorisation des particules du sol en fonction de leur diam tre. Les particules du sol sont g n ralement class es en trois cat gories principales :
Sable : Les plus grosses particules, avec des diam tres allant de 0,05 mm 2 mm.
Limon : Particules de taille interm diaire, allant de 0,002 mm 0,05 mm.
Argile : Les plus petites particules, avec des diam tres inf rieurs 0,002 mm.
- Les proportions relatives de ces fractions de taille d terminent la texture du sol, qui, son tour, affecte ses propri t s telles que la r tention d'eau et le drainage.
Tailles des Tamis:
- Les tailles des tamis sont des tailles de mailles normalis es utilis es pour s parer les particules du sol en fonction de leur taille. Les tailles de tamis courantes sont d finies par les normes ASTM (Soci t am ricaine pour les essais et les mat riaux) ou ISO (Organisation internationale de normalisation).
- L'analyse granulom trique consiste faire passer un chantillon de sol travers un ensemble de tamis de mailles de plus en plus fines pour d terminer la distribution de la taille des particules.
Nombre de Grains par mg:
- Cette m trique repr sente la densit des particules du sol dans une masse donn e de sol. Elle est calcul e en comptant le nombre de particules dans une masse connue de sol (g n ralement 1 mg) puis en extrapolant pour estimer le nombre total de particules dans un chantillon plus important.
- Elle fournit des informations sur la population et l'espacement des particules du sol, ce qui peut tre essentiel pour comprendre la compaction du sol et la p n tration des racines.
Vitesse de S dimentation:
- La vitesse de s dimentation fait r f rence la vitesse laquelle les particules du sol tombent travers un fluide (g n ralement de l'eau) sous l'influence de la gravit . Elle est d termin e par la taille, la forme et la densit des particules ainsi que par la viscosit du fluide.
- La connaissance des vitesses de s dimentation est pr cieuse dans les tudes de s dimentation et peut aider pr dire combien de temps il faut aux particules pour se d poser hors de la suspension dans les plans d'eau.
Vitesse de seuil pour la Traction:
- La vitesse de seuil pour la traction repr sente la vitesse minimale de l' coulement de l'eau n cessaire pour initier le mouvement des particules du sol sur le lit d'un ruisseau ou d'une rivi re. Il s'agit d'un param tre important dans les tudes sur le transport des s diments.
- Lorsque la vitesse de l'eau d passe la vitesse de seuil pour une taille de particule sp cifique, elle peut roder et transporter ces particules, ce qui peut avoir des implications environnementales significatives.
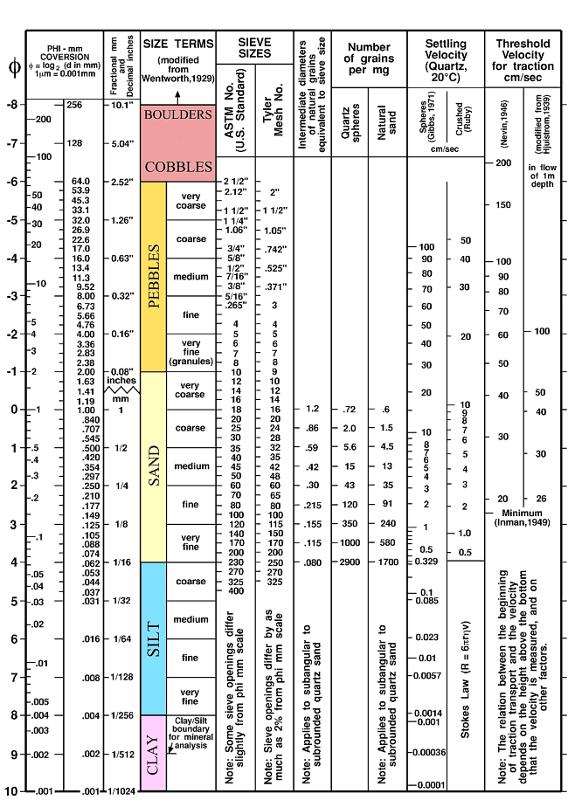
titre d'exemple, voici le graphique de la taille des particules mesur e dans le Long Island Sound par le Service g ologique des tats-Unis (USGS).
Le mod le peut tre d fini en fonction de l'existence de trois types de mat riaux (sable, limon et argile), avec des grains mod lis s comme suit : dans les deux premiers cas, les grains sont repr sent s sous forme de sph res avec diff rents rayons moyens, et dans le cas de l'argile, les grains sont mod lis s sous forme de parall l pip des droits.
Les plages de param tres sont r sum es dans le tableau suivant:
| Type | Param tre | Symbole | Plage | Unit |
| Ar ne | Radio | $r_a$ | 62 - 2000 | $\mu m$ |
| Volume | $v_a$ | 1 - 33500 | $nl$ | |
| Densit | $\rho_a$ | 2,64 - 2,69 | $g/cm^3$ | |
| Masse | $m_a$ | 2,6 - 90100 | $\mu g$ | |
| Boue | Rayon | $r_i$ | 4 - 62 | $\mu m$ |
| Volume | $v_i$ | 0,27 - 990 | $pl$ | |
| Densit | $\rho_i$ | 2,63 - 2,72 | $g/cm^3$ | |
| Masse | $m_i$ | 0,71 - 2700 | $ng$ | |
| Argile | Longueur | $l_c$ | 1 - 4 | $\mu m$ |
| Hauteur | $w_c$ | 0,1 - 0,4 | $\mu m$ | |
| Volume | $v_c$ | 0,1 - 6,4 | $fl$ | |
| Densit | $\rho_c$ | 2,66 - 2,80 | $g/cm^3$ | |
| Masse | $m_c$ | 0,27 - 17,9 | $pg$ |
Les grains tant si petits, il est n cessaire de travailler dans une large gamme de dimensions. Pour cette raison, des abr viations sont utilis es :
Long
| Symbole | Unit | MKS |
| M$ | m tre | 1 M$ |
| $mm$ | millim tre | $10^{-3} m$ |
| $\mu m$ | microm tre | $10^{-6} m$ |
Volume
| Symbole | Unit | MKS |
| $m^3$ | m tre cube | $1 m^3$ |
| $l$ | litre | $10^{-3} m^3$ |
| $ml$ | millilitre | $10^{-6} m^3$ |
| $\mu l$ | microlitre | $10^{-9} m^3$ |
| $nl$ | nanolitre | $10^{-12} m^3$ |
| $pl$ | picolitre | $10^{-15} m^3$ |
| $fl$ | fentolitre | $10^{-18} m^3$ |
Masse
| Symbole | Unit | MKS |
| $kg$ | kilogramme | $1 kg$ |
| $g$ | gramme | $10^{-3} kg$ |
| $mg$ | milligramme | $10^{-6} kg$ |
| $\mu g$ | microgramme | $10^{-9} kg$ |
| $ng$ | nanogramme | $10^{-12} kg$ |
| $pg$ | picogramme | $10^{-15} kg$ |
Densit
| Symbole | Unit | MKS |
| $kg/m^3$ | kilogramme par m tre cube | $1 kg/m^3$ |
| $g/cm^3$ | gramme par centim tre cube | $10^{3} kg/m^3$ |
Si nous mod lisons un grain de sable comme une sph re et supposons que le rayon du grain de sable ($r_a$), nous pouvons calculer son le volume d'un grain de sable ($v_a$) en utilisant l' quation suivante:
Ce calcul fournit une estimation du volume, car le rayon est une valeur moyenne. Pour obtenir un calcul plus pr cis ou m me d terminer un volume moyen, il serait n cessaire d' tudier la distribution des rayons des grains de sable dans l' tude.
Il est important de noter que le volume calcul n'est qu'une valeur de r f rence, car il est bas sur l'hypoth se que le sable est compos de sph res parfaites et identiques, ce qui n'est pas le cas dans la r alit .
Si nous mod lisons un grain de limon comme un parall l pip de droit et supposons que le côté grain de limon ($a_i$), nous pouvons calculer son le volume d'un grain de limon ($v_i$) en utilisant la suivante quation:
Cependant, il est important de noter que ce calcul fournit une valeur estim e du volume, car la longueur du c t est une valeur moyenne. Pour obtenir un calcul plus pr cis et m me d terminer un volume moyen, il serait n cessaire d' tudier la distribution des longueurs de c t des grains de limon dans l' tude.
Il convient de souligner que le volume calcul sert de valeur de r f rence, car il est bas sur l'hypoth se que le limon est compos de cubes parfaits et identiques, ce qui n'est pas le cas dans la r alit .
Si nous mod lisons un grain d'argile comme un parall l pip de droit et supposons qu'il a les dimensions le longueur et largeur d'une plaque d'argile ($l_c$) et a hauteur d'une plaque d'argile ($w_c$), nous pouvons calculer le volume d'un grain d'argile ($v_c$) en utilisant l' quation suivante:
Cependant, il est important de noter que ce calcul fournit une valeur estim e du volume, car les longueurs et la hauteur sont des valeurs moyennes. Pour obtenir un calcul plus pr cis et m me d terminer un volume moyen, il serait n cessaire d' tudier la distribution des longueurs et hauteurs des grains d'argile dans l' tude.
Il convient de souligner que le volume calcul sert de valeur de r f rence, car il est bas sur l'hypoth se que l'argile est compos e de parall l pip des rectangles parfaits et identiques, ce qui peut ne pas tre le cas dans la r alit .
Une fois que nous avons le volume d'un grain de sable ($v_a$) et a densité d'un grain de sable ($\rho_a$), nous pouvons d terminer a masse d'un grain de sable ($m_a$) en le calculant l'aide de l' quation suivante :
Cependant, il est important de rappeler que tant le volume que la densit du grain de sable sont des estimations, ce qui fait que la masse r sultante est principalement une valeur de r f rence. Pour effectuer un calcul plus pr cis, il serait n cessaire d' tudier la distribution des formes et des compositions min ralogiques pour obtenir une valeur moyenne plus exacte.
Il est pertinent de souligner que la masse calcul e sert de point de r f rence, car elle repose sur l'hypoth se que le sable est compos de sph res parfaites et que les densit s des grains sont identiques, ce qui n'est pas le cas dans la r alit .
Une fois que nous avons le volume d'un grain de limon ($v_i$) et a densité d'un grain de limon ($\rho_i$), nous pouvons d terminer a masse d'un grain de limon ($m_i$) en utilisant l' quation suivante :
Cependant, il est essentiel de se rappeler que tant le volume que la densit du grain de limon sont des estimations, ce qui fait que la masse r sultante est principalement une valeur de r f rence. Pour obtenir un calcul plus pr cis, il serait n cessaire d' tudier la distribution des formes et des compositions min ralogiques pour obtenir une valeur moyenne plus pr cise.
Il est important de souligner que la masse calcul e sert de point de r f rence, car elle repose sur l'hypoth se que le limon est compos de sph res parfaites et que les densit s des grains sont identiques, ce qui n'est pas le cas dans la r alit .
Une fois que nous disposons de le volume d'un grain d'argile ($v_c$) et a longueur et largeur d'une plaque d'argile ($\rho_c$), nous pouvons d terminer a masse d'une plaque d'argile ($m_c$) en utilisant l' quation suivante :
Cependant, il est essentiel de se rappeler que tant le volume que la densit du grain d'argile sont des estimations, ce qui fait que la masse r sultante est principalement une valeur de r f rence. Pour obtenir un calcul plus pr cis, il serait n cessaire d' tudier la distribution des formes et des compositions min ralogiques pour obtenir une valeur moyenne plus pr cise.
Il est important de souligner que la masse calcul e sert de point de r f rence, car elle repose sur l'hypoth se que l'argile est compos e de parall l pip des parfaits et que les densit s des grains sont identiques, ce qui n'est pas le cas dans la r alit .
ID:(362, 0)