Storyboard

En el caso del suelo, se puede modelar asumiendo que contiene múltiples poros que forman pequeños capilares que lo atraviesan. Con esta base, se pueden aplicar las ecuaciones para el flujo laminar a través de tubos y calcular las resistencias hidráulicas de las redes de capilares, que dependen de la porosidad y, por lo tanto, de la proporción de las distintas componentes.

>Modelo

ID:(370, 0)

Concepto

>Top

ID:(15203, 0)

Concepto

>Top

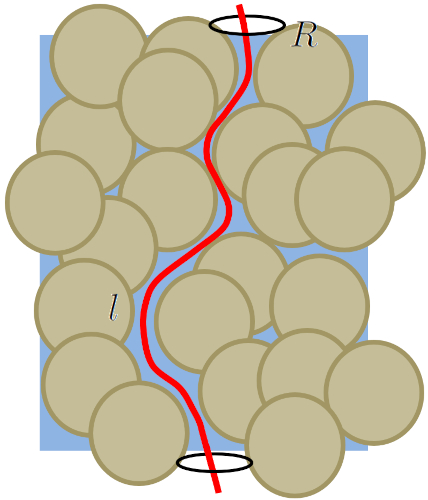
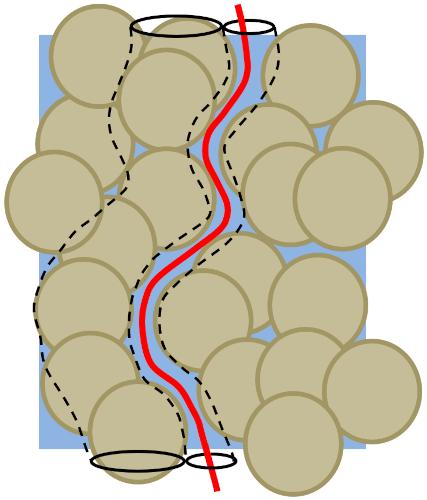
Los poros individuales se agrupan en cadenas que forman capilares por los cuales el agua circula.

Para modelar este fenómeno, es necesario estimar tanto el radio de estos capilares como su longitud, teniendo en cuenta que no suelen ser rectos.

ID:(937, 0)

Concepto

>Top

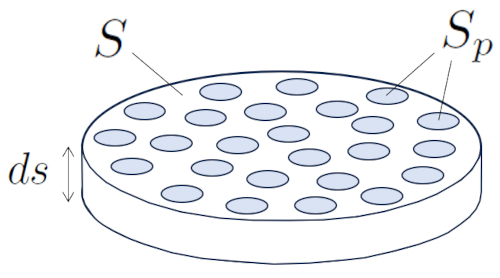
Si se toma una sección del flujo ($S$) de una altura la distancia infinitesimal ($ds$)

se tendra que el volumen será

$S ds$

meintras los poros ocuparan un volumen

$S_p ds$

lo que permite calcular la porosidad.

ID:(2284, 0)

Concepto

>Top

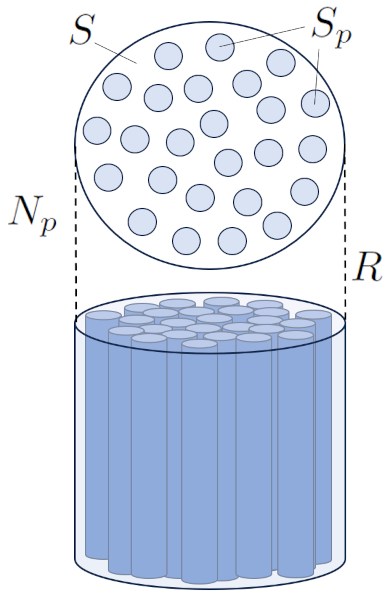
La sección del flujo ($S$) incluye la sección de poros ($S_p$) generada por el número de capilares ($N_p$):

ID:(2285, 0)

Concepto

>Top

Si observamos una sección transversal del suelo, notaremos que los capilares atraviesan los espacios entre los granos. Al hacerlo, su número es similar al de los mismos granos, por lo que podemos suponer que el número de capilares ($N_p$) es similar al número de granos presentes en la sección:

Poros en el Suelo

ID:(2283, 0)

Concepto

>Top

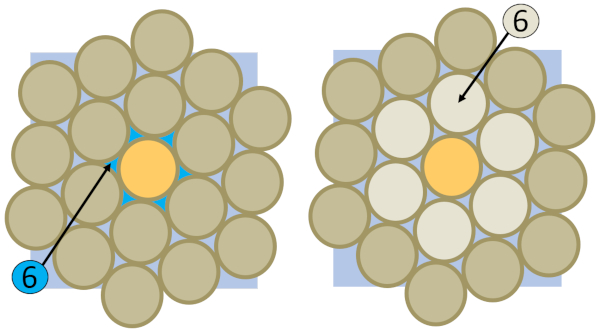
Si se compara el volumen del capilar con el de los granos del suelos se encontrara que en el suelo compactado los capilares son formados por la porosidad propia genérica ($q_0$) de los granos esta en esa misma relación con el volumen de los granos.

Por ello se puede establecer una relación entre ambos volumenes e igualados a la porosidad propia genérica ($q_0$) lo que permite generar una relación que permite calcular la largo del capilar ($l$).

ID:(2291, 0)

Concepto

>Top

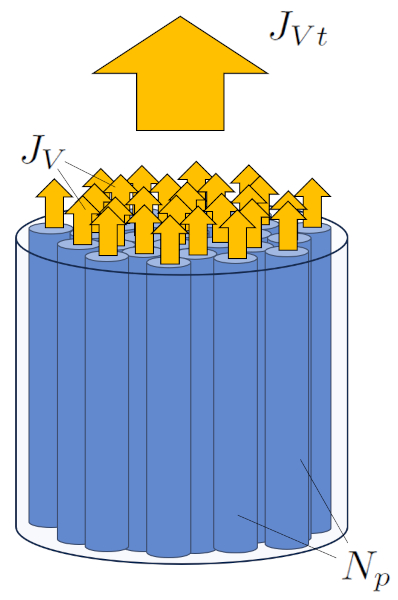
El flujo total se calcula como la suma de los flujos individuales a través de los distintos poros:

Si asumimos que todos los poros son idénticos, podemos obtener el flujo total ($J_{Vt}$) multiplicando el flujo de volumen ($J_V$) individualmente por el número de capilares ($N_p$).

ID:(2286, 0)

Ecuación

>Top, >Modelo

El flujo de líquido en un medio poroso como el suelo se mide mediante la variable la densidad de flujo ($j_s$), que representa la velocidad media a la que el líquido se desplaza a través de este medio. Al modelar el suelo y el paso del líquido a través de él, se descubre que este proceso está influenciado por factores como la porosidad ($f$) y el radio de un grano genérico ($r_0$), que, al ser mayores, facilitan el flujo, mientras que la viscosidad ($\eta$) dificulta el paso a través de los capilares, lo que reduce la velocidad de flujo.

El modelo finalmente incorpora lo que llamaremos la conductividad hidráulica ($K_s$), una variable que depende de las interacciones entre el radio de un grano genérico ($r_0$), la porosidad ($f$), la densidad del líquido ($\rho_w$), la aceleración gravitacional ($g$), la viscosidad ($\eta$) y la porosidad propia genérica ($q_0$):

$ K_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }$

Condiciones

Variables

$J_1$

Factor de volumen propio de la arena

$-$

$J_2$

Factor de volumen propio del limo

$-$

$J_t$

Flujo total 2 capas

$m^3/s$

Relación

Desarrollo

Dado que la densidad de flujo ($j_s$) está relacionado con el radio de un grano genérico ($r_0$), la porosidad ($f$), la densidad del líquido ($\rho_w$), la aceleración gravitacional ($g$), la viscosidad ($\eta$), la porosidad propia genérica ($q_0$), la diferencia de altura ($\Delta h$) y el largo de la muestra ($\Delta L$) a través de la ecuación

$ j_s =-\displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }\displaystyle\frac{ \Delta h }{ \Delta L }$

Podemos definir un factor al que llamaremos la conductividad hidráulica ($K_s$) de la siguiente manera:

$ K_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }$

Este factor incorpora todos los elementos relacionados con las propiedades del suelo y del líquido que fluye a través de él.

la conductividad hidráulica ($K_s$) expresa la facilidad con la que el líquido se conduce a través del medio poroso. De hecho, la conductividad hidráulica ($K_s$) aumenta con la porosidad ($f$) y el radio de un grano genérico ($r_0$), y disminuye con la porosidad propia genérica ($q_0$) y la viscosidad ($\eta$).

ID:(4739, 0)

Imagen

>Top

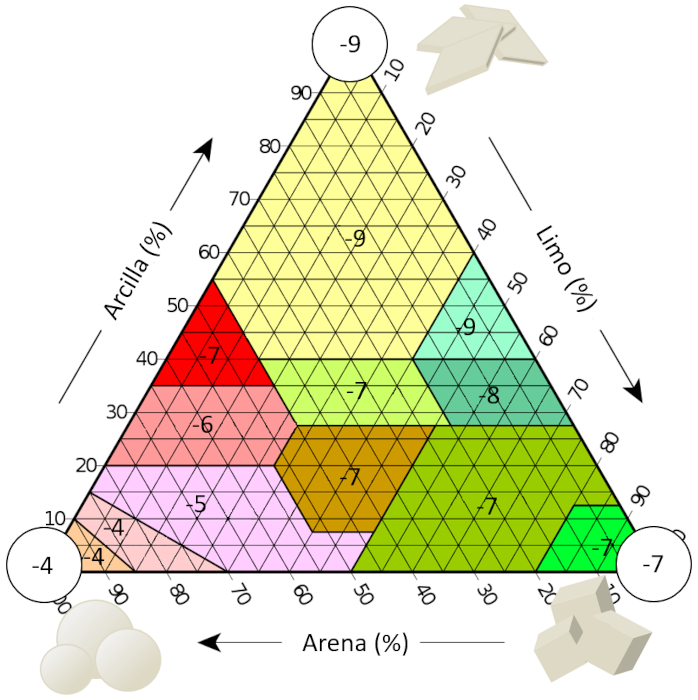
Si examinamos la literatura, podemos encontrar estimaciones de la conductividad hidráulica para diferentes texturas de suelo, que se muestran aquí en función de su exponente (es decir, se indica -7 para una conductividad hidráulica de 1E-7 m/s):

Los resultados se resumen en la siguiente tabla:

Estos datos se obtuvieron de la siguiente literatura, que se referencia en la columna de conductividad hidráulica:

[1] "Geotechnical Engineering Principles and Practices" de Donald P. Coduto et al., Prentice Hall (1999)

[2] "Soil Mechanics and Foundations" de Muni Budhu, John Wiley & Sons. (2011)

[3] "Introduction to Environmental Engineering" de Mackenzie Davis y David Cornwell, McGraw Hill (2022)

[4] "Principles of Geotechnical Engineering" de Braja M. Das, CL-Engineering (2009)

[5] "Soil Mechanics in Engineering Practice" de Karl Terzaghi y Ralph B. Peck, John Wiley & Sons. (1996)

[6] "Soil Mechanics: Concepts and Applications" de William Powrie, CRC Press (2013)

ID:(4740, 0)

Concepto

>Top

Parámetro seleccionado

Cálculos

ID:(15222, 0)

Ecuación

>Top, >Modelo

La porosidad ($f$) se puede calcular a partir de la sección de poros ($S_p$) y la sección del flujo ($S$) utilizando la siguiente fórmula:

$ f = \displaystyle\frac{ S_p }{ S }$

Condiciones

Variables

Relación

Desarrollo

Con la altura la distancia infinitesimal ($ds$), el volumen de la sección del flujo ($S$) es

$S ds$

y el de los poros con la sección de poros ($S_p$) es

$S_p ds$

por lo tanto, la porosidad ($f$) se calcula como

$f = \displaystyle\frac{S_p ds}{S ds} = \displaystyle\frac{S_p}{S}$

lo que resulta en la siguiente ecuación:

$ f = \displaystyle\frac{ S_p }{ S }$

ID:(938, 0)

Ecuación

>Top, >Modelo

Dado que la sección de un poro de radio del cilindro ($R$) es $\pi R^2$ y el número de capilares ($N_p$) está relacionado con eso, podemos calcular la sección de poros ($S_p$) de la siguiente manera:

$ S_p = N_p \pi R ^2$

Condiciones

Variables

$N_p$

Número de capilares

$-$

$\pi$

Pi

3.1415927

$rad$

$R$

Radio de la porosidad

$m$

$S_p$

Sección de poros

$m^2$

Relación

ID:(4362, 0)

Ecuación

>Top, >Modelo

Usando la porosidad ($f$) y la sección del flujo ($S$), obtenemos la sección de poros ($S_p$), que al dividirlo por la sección del capilar calculada de el radio del cilindro ($R$), resulta en el número de capilares ($N_p$) de acuerdo con:

$ N_p =\displaystyle\frac{ f S }{ \pi R ^2}$

Condiciones

Variables

$N_p$

Número de capilares

$-$

$\pi$

Pi

3.1415927

$rad$

$f$

Porosidad

$-$

$R$

Radio de la porosidad

$m$

$S_t$

Sección del suelo

$m^2$

Relación

Desarrollo

Como la porosidad ($f$), calculado con la sección de poros ($S_p$) y la sección del flujo ($S$) usando

$ f = \displaystyle\frac{ S_p }{ S }$

junto con la ecuación para el cálculo de la sección de poros ($S_p$) en función de el número de capilares ($N_p$) y el radio del cilindro ($R$) mediante

$ S_p = N_p \pi R ^2$

con lo cual se obtiene

$f = \displaystyle\frac{N_p\pi R^2}{S}$

se puede despejar el número de capilares ($N_p$) resultando en

$ N_p =\displaystyle\frac{ f S }{ \pi R ^2}$

ID:(4363, 0)

Ecuación

>Top, >Modelo

Si asumimos que el número de capilares es igual al número de granos visibles en una sección, podemos demostrar que para un radio de un grano de el radio de un grano genérico ($r_0$) y una porosidad ($f$), el radio del cilindro ($R$) será igual a:

$R = \sqrt{\displaystyle\frac{ f }{1- f }} r_0 $

Condiciones

Variables

Relación

Desarrollo

Si consideramos el área en la sección que no contiene poros, restando la sección de poros ($S_p$) de la sección del flujo ($S$) y dividiendo por el área de un grano genérico de radio de un grano genérico ($r_0$), obtenemos el número de granos visibles en el corte:

$\displaystyle\frac{S-S_p}{\pi r_0^2}=\displaystyle\frac{(1-f)S}{\pi r_0^2}$

donde utilizamos la relación para la porosidad ($f$):

$ f = \displaystyle\frac{ S_p }{ S }$

Si el número de granos es igual a número de capilares ($N_p$) con la expresión:

$ N_p =\displaystyle\frac{ f S }{ \pi R ^2}$

donde el radio es el radio del cilindro ($R$). Con esto, obtenemos la relación:

$\displaystyle\frac{(1-f)S}{\pi r_0^2}=\displaystyle\frac{fS}{\pi R^2}$

lo que resulta en:

$R = \sqrt{\displaystyle\frac{ f }{1- f }} r_0 $

ID:(109, 0)

Ecuación

>Top, >Modelo

Si igualamos el volumen de un capilar al volumen de una cadena de granos multiplicado por el largo de la muestra ($\Delta L$), obtenemos una relación entre la largo del capilar ($l$) y la porosidad ($f$) dada por:

$ l = q_0 \displaystyle\frac{(1- f )}{ f } \Delta L $

Condiciones

Variables

Relación

Desarrollo

El volumen del capilar se puede calcular a partir de el radio del cilindro ($R$) y la largo del capilar ($l$), lo cual es igual al volumen de una cadena de granos de el radio de un grano genérico ($r_0$) y el largo de tubo ($\Delta L$) multiplicado por la porosidad propia genérica ($q_0$):

$\pi R^2 l = q_0 \pi r_0^2 \Delta L$

Esto, en conjunto con la porosidad ($f$) en la relación

$R = \sqrt{\displaystyle\frac{ f }{1- f }} r_0 $

resulta en la siguiente relación:

$ l = q_0 \displaystyle\frac{(1- f )}{ f } \Delta L $

ID:(2215, 0)

Ecuación

>Top, >Modelo

El flujo total ($J_{Vt}$) se calcula multiplicando un número de capilares ($N_p$) por el valor de el flujo de volumen ($J_V$) en cada capilar, de la siguiente manera:

$ J_{Vt} = N_p J_V $

Condiciones

Variables

$J_V$

Flujo según Hagen-Poiseville

$m^3/s$

$J_{Vt}$

Flujo total

$m^3/s$

$N_p$

Número de capilares

$-$

Relación

ID:(4364, 0)

Ecuación

>Top, >Modelo

Si aplicamos la ecuación de Hagen-Poiseuille a el flujo de volumen ($J_V$) para el caso de capilares con el radio del cilindro ($R$) expresados en términos de la porosidad ($f$) y la largo del capilar ($l$) como función de el largo de la muestra ($\Delta L$), podemos calcular el flujo total ($J_{Vt}$) utilizando

El resultado puede expresarse en términos de la sección del flujo ($S$), la viscosidad ($\eta$), la porosidad propia genérica ($q_0$), el radio de un grano genérico ($r_0$) y la diferencia de presión ($\Delta p$):

$ J_{Vt} =-\displaystyle\frac{ r_0 ^2}{8 \eta q_0 }\displaystyle\frac{ f ^3}{(1- f )^2}\displaystyle\frac{ S }{ \Delta L } \Delta p $

Condiciones

Variables

$\Delta p_2$

Diferencia de presión 2

$Pa$

$J_{Vt}$

Flujo según ley de Hagen Poiseville para suelo

$m^3/s$

$L$

Largo del capilar

$m$

$f$

Porosidad

$-$

$R$

Radio de la porosidad

$m$

$S_t$

Sección del suelo

$m^2$

$\eta_w$

Viscosidad del agua

$Pa s$

Relación

Desarrollo

Para calcular el flujo total ($J_{Vt}$) utilizando el número de capilares ($N_p$) y el flujo de volumen ($J_V$) para cada capilar a través de

$ J_{Vt} = N_p J_V $

obtenemos el número de capilares ($N_p$) con la porosidad ($f$), la sección del flujo ($S$) y el radio del cilindro ($R$) mediante

$ N_p =\displaystyle\frac{ f S }{ \pi R ^2}$

y la ley de Hagen-Poiseuille utilizando la viscosidad ($\eta$), la diferencia de presión ($\Delta p$) y la largo del capilar ($l$) se calcula con

$J_v = - \displaystyle\frac{\pi R^4}{8\eta}\displaystyle\frac{\Delta p}{l}$

Utilizando la relación para el radio del cilindro ($R$) en términos de el radio de un grano genérico ($r_0$)

$R = \sqrt{\displaystyle\frac{ f }{1- f }} r_0 $

y para la largo del capilar ($l$), la porosidad propia genérica ($q_0$), y el largo de la muestra ($\Delta L$)

$ l = q_0 \displaystyle\frac{(1- f )}{ f } \Delta L $

obtenemos

$ J_{Vt} =-\displaystyle\frac{ r_0 ^2}{8 \eta q_0 }\displaystyle\frac{ f ^3}{(1- f )^2}\displaystyle\frac{ S }{ \Delta L } \Delta p $

Esta ecuación corresponde a la ecuación de Kozeny-Carman, que fue desarrollada por Kozeny y Carman para modelar el flujo de un líquido a través de un medio poroso y se publicó en:

• Sobre la conducción capilar del agua en el suelo., ("Ueber kapillare Leitung des Wassers im Boden."), J. Kozeny, Sitzungsber Akad. Wiss., Wien, 136(2a): 271-306 (1927)

• Flujo de fluidos a través de lechos granulares., ("Fluid flow through granular beds."), P.C. Carman, Transactions, Institution of Chemical Engineers, London, 15: 150-166 (1937)

• Flujo de gases a través de medios porosos., ("Flow of gases through porous media."), P.C. Carman, Butterworths, London (1956)

ID:(4365, 0)

Ecuación

>Top, >Modelo

Como la conductancia hidráulica ($G_h$) está relacionado con la sección del flujo ($S$), el radio de un grano genérico ($r_0$), la viscosidad ($\eta$), la porosidad propia genérica ($q_0$), la porosidad ($f$) y el largo de la muestra ($\Delta L$), mediante

y dado que la conductancia hidráulica ($G_h$) es el inverso de la resistencia hidráulica ($R_h$), podemos afirmar que

$ R_h = \displaystyle\frac{8 \eta q_0 }{ r_0 ^2}\displaystyle\frac{(1- f )^2 }{f ^3}\displaystyle\frac{ \Delta L }{ S }$

Condiciones

Variables

$S_1$

Sección en el punto 1

$m^2$

$S_2$

Sección en el punto 2

$m^2$

$S$

Sección o superficie

$m^2$

Relación

Desarrollo

Usando la Ley de Darcy, donde la diferencia de presión ($\Delta p$) se iguala a la resistencia hidráulica ($R_h$) y el flujo total ($J_{Vt}$):

$ \Delta p = R_h J_V $

Así, con la ecuación para el suelo con la sección del flujo ($S$), el radio de un grano genérico ($r_0$), la viscosidad ($\eta$), la porosidad propia genérica ($q_0$), la porosidad ($f$), la diferencia de presión ($\Delta p$) y el largo de la muestra ($\Delta L$):

$ J_{Vt} =-\displaystyle\frac{ r_0 ^2}{8 \eta q_0 }\displaystyle\frac{ f ^3}{(1- f )^2}\displaystyle\frac{ S }{ \Delta L } \Delta p $

Entonces, la resistencia hidráulica ($R_h$) es:

$ R_h = \displaystyle\frac{8 \eta q_0 }{ r_0 ^2}\displaystyle\frac{(1- f )^2 }{f ^3}\displaystyle\frac{ \Delta L }{ S }$

ID:(10594, 0)

Ecuación

>Top, >Modelo

En el caso de un tubo por el cual un líquido con la densidad del agua ($\rho_w$) fluye debido a la diferencia de presión ($\Delta p$) generado por una una diferencia de altura ($\Delta h$) bajo la influencia de la gravedad representada por la aceleración gravitacional ($g$) y calculado con la ecuación:

esto puede emplearse en la ecuación de Hagen-Poiseuille, junto con la definición de la densidad de flujo ($j_s$) en términos de el flujo total ($J_{Vt}$), que a su vez depende de el radio de un grano genérico ($r_0$), la porosidad propia genérica ($q_0$), la porosidad ($f$), la viscosidad ($\eta$) y el largo de la muestra ($\Delta L$):

$ j_s =-\displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }\displaystyle\frac{ \Delta h }{ \Delta L }$

Condiciones

Variables

$\rho_w$

Densidad del líquido

$kg/m^3$

$\Delta h$

Diferencia de altura o profundidad

$m$

$J_{Vt}$

Flujo por la muestra

$m^3/s$

$L$

Largo del capilar

$m$

$f$

Porosidad

$-$

$R$

Radio de la porosidad

$m$

$S_t$

Sección del suelo

$m^2$

$\eta_w$

Viscosidad del agua

$Pa s$

Relación

Desarrollo

En el caso de los capilares por los cuales un líquido de la densidad del líquido ($\rho_w$) fluye debido a la diferencia de presión ($\Delta p$) generado por una diferencia de altura ($\Delta h$) bajo la influencia de la gravedad representada por la aceleración gravitacional ($g$) y calculado con la ecuación:

$ \Delta p = \rho_w g \Delta h $

esto puede ser aplicado en la ecuación de Hagen-Poiseuille, en términos de el flujo total ($J_{Vt}$), que a su vez depende de el radio de un grano genérico ($r_0$), la porosidad propia genérica ($q_0$), la porosidad ($f$), la viscosidad ($\eta$), la sección o superficie ($S$) y el largo de la muestra ($\Delta L$) como se describe en la ecuación:

$ J_{Vt} =-\displaystyle\frac{ r_0 ^2}{8 \eta q_0 }\displaystyle\frac{ f ^3}{(1- f )^2}\displaystyle\frac{ S }{ \Delta L } \Delta p $

Junto con la definición de la densidad de flujo ($j_s$):

$j_s = \displaystyle\frac{J_{Vt}}{S}$

Tenemos:

$j_s=\displaystyle\frac{J_{Vt}}{S}=\displaystyle\frac{ r_0 ^2 }{8 q_g }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }\displaystyle\frac{ \Delta h }{ L }$

lo que resulta en:

$ j_s =-\displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }\displaystyle\frac{ \Delta h }{ \Delta L }$

ID:(4366, 0)

Ecuación

>Top, >Modelo

Para relacionar la conductividad hidráulica con los factores de masa, introducimos el factor de escala de capilares ($\gamma$) junto con el radio de un grano genérico ($r_0$), el radio del grano de arena ($r_a$), la porosidad propia genérica ($q_0$) y la porosidad propia de la arena ($q_a$) como

$ \gamma = \displaystyle\frac{ r_0 ^2}{ r_a ^2}\displaystyle\frac{ q_a }{ q_0 }$

Condiciones

Variables

Relación

.

ID:(15101, 0)

Ecuación

>Top, >Modelo

A partir de la definición de la conductividad hidráulica ($K_s$) y el factor de escala de capilares ($\gamma$), podemos expresar la conductividad hidráulica ($K_s$) en función de el radio del grano de arena ($r_a$), la porosidad propia de la arena ($q_a$), la porosidad ($f$), la densidad del líquido ($\rho_w$), la aceleración gravitacional ($g$) y la viscosidad ($\eta$) de la siguiente manera:

$ K_s = \displaystyle\frac{ r_a ^2}{8 q_a }\displaystyle\frac{ f ^3}{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta } \gamma $

Condiciones

Variables

Relación

ID:(977, 0)

Ecuación

>Top, >Modelo

El cálculo de el factor de escala de capilares ($\gamma$) se obtiene a partir de la porosidad ($f$), la densidad del líquido ($\rho_w$), la aceleración gravitacional ($g$), y la viscosidad ($\eta$) eliminando el radio del grano de arena ($r_a$) y la porosidad propia de la arena ($q_a$) mediante la siguiente ecuación:

$\gamma=\displaystyle\frac{8K_sq_a}{r_a^2}\displaystyle\frac{(1-f)^2}{f^3}\displaystyle\frac{\eta}{\rho_wg}$

Si deseamos relacionar el factor de escala de capilares ($\gamma$) con la fracción de masa de arena en la muestra ($g_a$), la fracción de masa de limo en la muestra ($g_i$) y la fracción de masa de arcilla en la muestra ($g_c$), notamos que mientras el primero varía en 6 potencias, los segundos varían solo en 2, lo que justifica establecer una relación con el logaritmo natural de $\gamma$. Por lo tanto, realizamos una regresión utilizando la ecuación:

$\ln \gamma = s_a g_a + s_i g_i + s_c g_c $

Condiciones

Variables

Relación

con el factor de sección del capilar en arena ($s_a$), el factor de sección del capilar en limo ($s_i$), y el factor de sección del capilar en arcilla ($s_c$).

Los datos medios para cada rango son los siguientes:

La regresión resulta en una relación lineal con un R cuadrado de 0.9975 y los siguientes coeficientes, junto con los valores para evaluar la calidad de los coeficientes:

Dado los valores del p-test, podemos asumir que todos los coeficientes son altamente relevantes.

ID:(15100, 0)