Traversez plusieurs couches
Storyboard 
Une fois que la résistance hydraulique et la conductivité ont été calculées, il devient possible de modéliser un système de sol à plusieurs couches. Pour cela, il est essentiel de calculer la résistance totale et la conductivité totale, puis, après avoir établi le flux global, de déterminer les flux partiels (dans le cas de couches parallèles) ou la chute de pression dans chaque couche (dans le cas de couches en série).
ID:(371, 0)
Traversez plusieurs couches
Storyboard 
Une fois que la résistance hydraulique et la conductivité ont été calculées, il devient possible de modéliser un système de sol à plusieurs couches. Pour cela, il est essentiel de calculer la résistance totale et la conductivité totale, puis, après avoir établi le flux global, de déterminer les flux partiels (dans le cas de couches parallèles) ou la chute de pression dans chaque couche (dans le cas de couches en série).
Variables
Calculs
Calculs
Équations
Le volumique flux ($J_V$) peut tre calcul partir de a conductance hydraulique ($G_h$) et a différence de pression ($\Delta p$) en utilisant l' quation suivante :
De plus, en utilisant la relation pour a résistance hydraulique ($R_h$) :
on obtient :
Une mani re de mod liser un tube dont la section varie consiste le diviser en sections de rayon constant, puis additionner les r sistances hydrauliques en s rie. Supposons que nous avons une s rie de a resistência hidráulica em uma rede ($R_{hk}$), qui d pend de a viscosité ($\eta$), le rayon du cylindre k ($R_k$), et le longueur du tube k ($\Delta L_k$) via l' quation suivante :
Dans chaque segment, il y aura une différence de pression dans un réseau ($\Delta p_k$) avec a resistência hidráulica em uma rede ($R_{hk}$) et le volumique flux ($J_V$) auxquels la loi de Darcy est appliqu e :
a différence de pression totale ($\Delta p_t$) sera gal la somme des ERROR:10132,0 individuels :
donc,
$\Delta p_t=\displaystyle\sum_k \Delta p_k=\displaystyle\sum_k (R_{hk}J_V)=\left(\displaystyle\sum_k R_{hk}\right)J_V\equiv R_{st}J_V$
Ainsi, le syst me peut tre mod lis comme un conduit unique avec la r sistance hydraulique calcul e comme la somme des composantes individuelles :
A conductance hydraulique totale parallèle ($G_{pt}$) combin avec a conductance hydraulique dans un réseau ($G_{hk}$) dans
et associ a resistência hidráulica em uma rede ($R_{hk}$) ainsi qu' l' quation
m ne a résistance hydraulique totale en parallèle ($R_{pt}$) via
A résistance hydraulique totale en série ($R_{st}$), ainsi que a resistência hidráulica em uma rede ($R_{hk}$), dans
et avec a conductance hydraulique dans un réseau ($G_{hk}$) et l' quation
conduit au fait que a conductance hydraulique de la série totale ($G_{st}$) peut tre calcul avec
Avec le flux total ($J_{Vt}$) tant gal le débit volumique dans un réseau ($J_{Vk}$) :
et avec a différence de pression ($\Delta p$) et a conductance hydraulique dans un réseau ($G_{hk}$), ainsi que l' quation
pour chaque l ment, nous en arrivons la conclusion que, avec a conductance hydraulique totale parallèle ($G_{pt}$),
$J_{Vt}=\displaystyle\sum_k J_{Vk} = \displaystyle\sum_k G_{hk}\Delta p = G_{pt}\Delta p$
nous avons
tant donn que a densité de flux ($j_s$) est li le rayon d'un grain générique ($r_0$), a porosité ($f$), a densité du liquide ($\rho_w$), a accélération gravitationnelle ($g$), a viscosité ($\eta$), a porosité propre générique ($q_0$), a différence de hauteur ($\Delta h$) et le longueur de l'échantillon ($\Delta L$) travers l' quation :
Nous pouvons d finir un facteur que nous appellerons a conductivité hydraulique ($K_s$) comme suit :
Ce facteur englobe tous les l ments li s aux propri t s du sol et du liquide qui s' coule travers lui.
Comme a résistance hydraulique ($R_h$) est associ a conductivité hydraulique ($K_s$), a densité du liquide ($\rho_w$), a accélération gravitationnelle ($g$), a hauteur de la colonne de liquide ($S$) et le longueur de l'échantillon ($\Delta L$), il s'exprime comme suit :
Et la relation pour a conductance hydraulique ($G_h$)
m ne
Avec la loi de Darcy, o a différence de pression ($\Delta p$) est gal a résistance hydraulique ($R_h$) et le flux total ($J_{Vt}$) :
Ainsi, avec l' quation pour le sol avec a coupe des pores ($S$), le rayon d'un grain générique ($r_0$), a viscosité ($\eta$), a porosité propre générique ($q_0$), a porosité ($f$), a différence de pression ($\Delta p$) et le longueur de l'échantillon ($\Delta L$) :
Par cons quent, a résistance hydraulique ($R_h$) est :
En calculant a résistance hydraulique ($R_h$) en utilisant a viscosité ($\eta$), a porosité propre générique ($q_0$), le rayon d'un grain générique ($r_0$), a porosité ($f$), le longueur de l'échantillon ($\Delta L$), et a hauteur de la colonne de liquide ($S$) travers
et en utilisant l'expression pour a conductivité hydraulique ($K_s$)
est obtenu apr s le remplacement des facteurs communs
Si nous examinons la loi de Hagen-Poiseuille, qui nous permet de calculer le volumique flux ($J_V$) partir de le rayon du tube ($R$), a viscosité ($\eta$), le longueur du tube ($\Delta L$) et a différence de pression ($\Delta p$) :
nous pouvons introduire a conductance hydraulique ($G_h$), d fini en termes de le longueur du tube ($\Delta L$), le rayon du tube ($R$) et a viscosité ($\eta$), de la mani re suivante :
pour obtenir :
Exemples
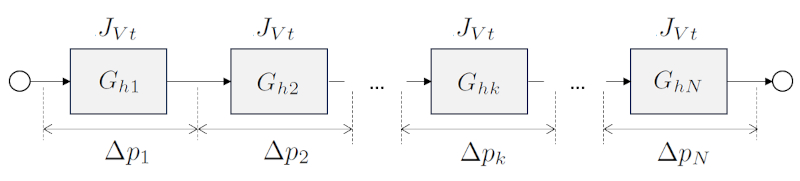
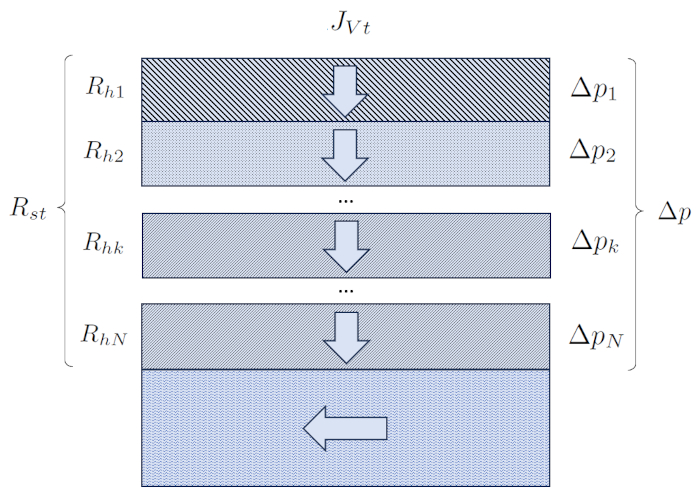
Dans le cas d'une somme o les l ments sont connect s en s rie, la r sistance hydraulique totale du syst me est calcul e en additionnant les r sistances individuelles de chaque l ment.
Une mani re de mod liser un tube dont la section varie consiste le diviser en sections de rayon constant, puis additionner les r sistances hydrauliques en s rie. Supposons que nous avons une s rie de a resistência hidráulica em uma rede ($R_{hk}$), qui d pend de a viscosité ($\eta$), le rayon du cylindre k ($R_k$), et le longueur du tube k ($\Delta L_k$) via l' quation suivante :
Dans chaque segment, il y aura une différence de pression dans un réseau ($\Delta p_k$) avec a resistência hidráulica em uma rede ($R_{hk}$) et le volumique flux ($J_V$) auxquels la loi de Darcy est appliqu e :
a différence de pression totale ($\Delta p_t$) sera gal la somme des ERROR:10132,0 individuels :
donc,
$\Delta p_t=\displaystyle\sum_k \Delta p_k=\displaystyle\sum_k (R_{hk}J_V)=\left(\displaystyle\sum_k R_{hk}\right)J_V\equiv R_{st}J_V$
Ainsi, le syst me peut tre mod lis comme un conduit unique avec la r sistance hydraulique calcul e comme la somme des composantes individuelles :
Dans le cas d'une somme o les l ments sont connect s en s rie, la conductance hydraulique totale du syst me est calcul e en additionnant les conductances hydrauliques individuelles de chaque l ment.
a résistance hydraulique totale en série ($R_{st}$), ainsi que a resistência hidráulica em uma rede ($R_{hk}$), dans
et avec a conductance hydraulique dans un réseau ($G_{hk}$) et l' quation
conduit au fait que a conductance hydraulique de la série totale ($G_{st}$) peut tre calcul avec
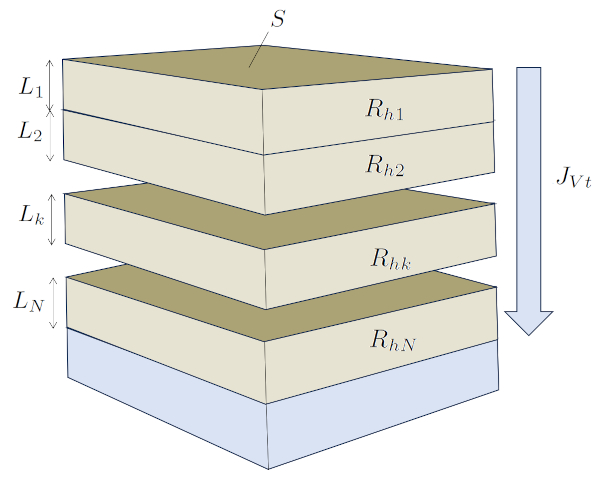
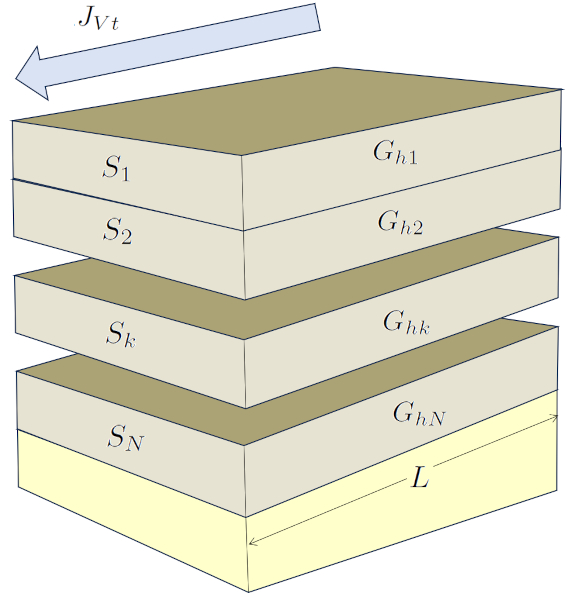
Une situation dans le sol o les l ments sont connect s en s rie se produit lorsque l'eau s'infiltre verticalement travers plusieurs couches pour finalement atteindre la nappe phr atique. Dans ce cas, a hauteur de la colonne de liquide ($S$) reste constant, tandis que chaque couche a une largeur diff rente qui agit comme a largeur de la kème couche ($L_k$).
Dans cette situation, les r sistances hydrauliques sont directement additionn es, et leurs valeurs d pendent du type de sol, et donc de a conductivité hydraulique dans la kème couche ($K_{sk}$) et de a largeur de la kème couche ($L_k$).
Une mani re efficace de mod liser un tube section variable consiste le diviser en sections de rayon constant, puis additionner les r sistances hydrauliques en s rie. Supposons que nous ayons une s rie d' l ments a resistência hidráulica em uma rede ($R_{hk}$), dont la r sistance d pend de a viscosité ($\eta$), le rayon du cylindre k ($R_k$) et le longueur du tube k ($\Delta L_k$), selon l' quation suivante :
Dans chaque l ment, nous consid rons une différence de pression dans un réseau ($\Delta p_k$) ainsi que a resistência hidráulica em uma rede ($R_{hk}$) et le d bit volum trique le volumique flux ($J_V$), en appliquant la loi de Darcy :
La r sistance totale du syst me, le flux volumique total ($J_{Vt}$), est gale la somme des r sistances hydrauliques individuelles ERROR:10133,0 de chaque section :
Ainsi, nous avons :
$J_{Vt}=\displaystyle\sum_k \Delta J_{Vk}=\displaystyle\sum_k \displaystyle\frac{\Delta p_k}{R_{hk}}=\left(\displaystyle\sum_k \displaystyle\frac{1}{R_{hk}}\right)\Delta p\equiv \displaystyle\frac{1}{R_{pt}}J_V$
Par cons quent, le syst me peut tre mod lis comme un conduit unique avec une r sistance hydraulique totale calcul e en additionnant les composants individuels :
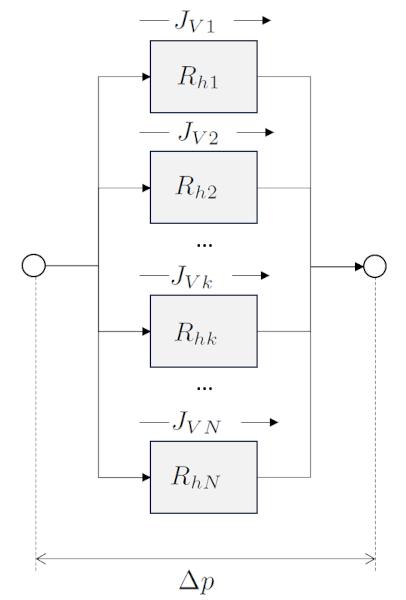
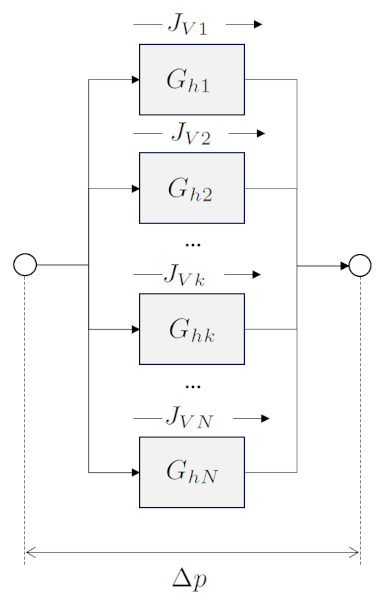
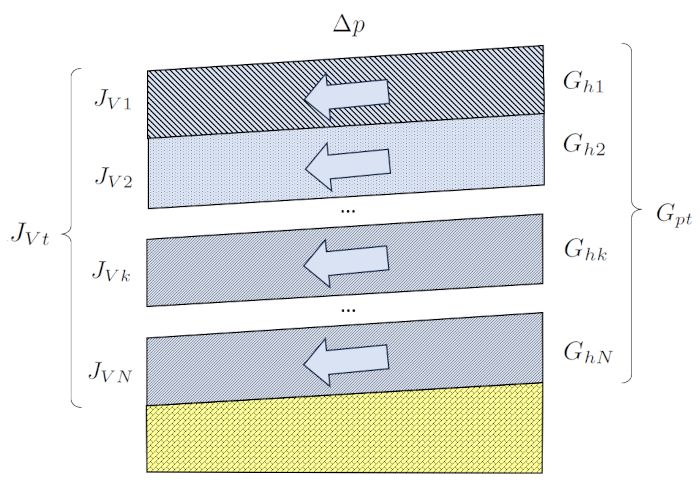
Le flux volumique total ($J_{Vt}$) repr sente la somme totale des contributions individuelles de le volumique flux 1 ($J_{V1}$) et le volumique flux 2 ($J_{V2}$), provenant des l ments connect s en parall le :
Une situation dans le sol o les l ments sont connect s en parall le se produit lorsque l'eau s' coule travers diff rentes couches en parall le. Si les couches ont une pente, une diff rence de pression est g n r e. Si les couches ont une paisseur similaire, la diff rence de pression sera la m me dans toutes les couches. Dans ce cas, le longueur de l'échantillon ($\Delta L$) est constant, tandis que chaque couche a une a section de la kème couche ($S_k$) diff rente.
Dans cette situation, les conductivit s hydrauliques sont directement additionn es, et leurs valeurs d pendent du type de sol, et donc de a conductivité hydraulique dans la kème couche ($K_{sk}$) et de a section de la kème couche ($S_k$).
Le flux de liquide dans un milieu poreux comme le sol est mesur l'aide de la variable a densité de flux ($j_s$), qui repr sente la vitesse moyenne laquelle le liquide se d place travers celui-ci. Lors de la mod lisation du sol et de la mani re dont le liquide le traverse, on constate que ce processus est influenc par des facteurs tels que a porosité ($f$) et le rayon d'un grain générique ($r_0$), qui, lorsqu'ils sont plus lev s, facilitent le flux, tandis que a viscosité ($\eta$) entrave le passage travers les capillaires, r duisant ainsi la vitesse d' coulement.
Le mod le int gre finalement ce que nous appellerons a conductivité hydraulique ($K_s$), une variable qui d pend des interactions entre le rayon d'un grain générique ($r_0$), a porosité ($f$), a densité du liquide ($\rho_w$), a accélération gravitationnelle ($g$), a viscosité ($\eta$) et a porosité propre générique ($q_0$) :
a conductivité hydraulique ($K_s$) exprime la facilit avec laquelle le liquide est conduit travers le milieu poreux. En fait, a conductivité hydraulique ($K_s$) augmente avec a porosité ($f$) et le rayon d'un grain générique ($r_0$), et diminue avec a porosité propre générique ($q_0$) et a viscosité ($\eta$).
Comme le flux total ($J_{Vt}$) est li le rayon d'un grain générique ($r_0$), a porosité ($f$), a densité du liquide ($\rho_w$), a accélération gravitationnelle ($g$), a viscosité ($\eta$), a porosité propre générique ($q_0$), a hauteur de la colonne de liquide ($S$) et le longueur de l'échantillon ($\Delta L$), il est gal :
Par cons quent, a conductance hydraulique ($G_h$) est gal :
Dans le contexte de la r sistance lectrique, son inverse existe, connu sous le nom de conductance lectrique. De mani re similaire, ce qui serait a conductance hydraulique ($G_h$) peut tre d fini en termes de a résistance hydraulique ($R_h$) travers l'expression :
En calculant a résistance hydraulique ($R_h$) avec a viscosité ($\eta$), a porosité propre générique ($q_0$), le rayon d'un grain générique ($r_0$), a porosité ($f$), le longueur de l'échantillon ($\Delta L$), et a hauteur de la colonne de liquide ($S$) en utilisant
qui peut tre r crite en utilisant l'expression pour a conductivité hydraulique ($K_s$) avec a densité du liquide ($\rho_w$) et a accélération gravitationnelle ($g$), ce qui donne
Comme a résistance hydraulique ($R_h$) est li a conductivité hydraulique ($K_s$), a densité du liquide ($\rho_w$), a accélération gravitationnelle ($g$), a hauteur de la colonne de liquide ($S$) et le longueur de l'échantillon ($\Delta L$), il s'exprime comme suit :
Puisque a conductance hydraulique ($G_h$) est l'inverse de a résistance hydraulique ($R_h$), nous pouvons conclure que
A différence de pression totale ($\Delta p_t$) par rapport aux diff rentes ERROR:10132,0, nous conduisant la conclusion suivante :
Darcy r crit l' quation de Hagen Poiseuille de sorte que a différence de pression ($\Delta p$) soit gal a résistance hydraulique ($R_h$) fois le volumique flux ($J_V$)xa0:
Lorsqu'il y a plusieurs r sistances hydrauliques connect es en s rie, nous pouvons calculer a résistance hydraulique totale en série ($R_{st}$) en ajoutant a resistência hidráulica em uma rede ($R_{hk}$), comme exprim dans la formule suivante :
Dans le cas de r sistances hydrauliques en s rie, l'inverse de a conductance hydraulique de la série totale ($G_{st}$) est calcul en additionnant les inverses de chaque a conductance hydraulique dans un réseau ($G_{hk}$) :
tant donn que chaque a résistance hydraulique de la kème couche ($R_{sk}$), qui d pend de a densité du liquide ($\rho_w$), a accélération gravitationnelle ($g$), a section de calque ($S$), a largeur de la kème couche ($L_k$) et a conductivité hydraulique dans la kème couche ($K_{sk}$), est
il en r sulte que a résistance hydraulique totale en série ($R_{st}$) est
La somme des couches de sol en parall le, not e le flux total ($J_{Vt}$), est gale la somme de le débit volumique dans un réseau ($J_{Vk}$) :
A conductance hydraulique totale parallèle ($G_{pt}$) est calcul avec la somme de a conductance hydraulique dans un réseau ($G_{hk}$)xa0:
Avec l'introduction de a conductance hydraulique ($G_h$), nous pouvons r crire l' quation de Hagen-Poiseuille avec a différence de pression ($\Delta p$) et le volumique flux ($J_V$) l'aide de l' quation suivante :
A résistance hydraulique totale en parallèle ($R_{pt}$) peut tre calcul comme l'inverse de la somme de a resistência hidráulica em uma rede ($R_{hk}$)xa0:
tant donn que chaque a conductance hydraulique dans un réseau ($G_{hk}$), d pendant de a densité du liquide ($\rho_w$), a accélération gravitationnelle ($g$), a longueur de la couche de sol ($L$), a section de la kème couche ($S_k$), et a conductivité hydraulique dans la kème couche ($K_{sk}$), est gal :
Par cons quent, a conductance hydraulique totale parallèle ($G_{pt}$) est calcul comme suit :
ID:(371, 0)