Pressão hidrostática
Storyboard 
No caso de solo saturado, a porosidade está completamente preenchida com água. A presença de água implica massa adicional e a existência de pressão em função da profundidade. Ambos os fatores afetarão o comportamento do solo.
ID:(368, 0)
Descrição da coluna d'água
Imagem 
Para estudar o comportamento de líquidos, é útil introduzir o conceito de uma coluna de líquido. Essa coluna é uma abstração de um recipiente cilíndrico (por exemplo, uma proveta) com líquido, permitindo estudar a força a que um objeto no interior dela está exposto.
Uma vez introduzido o conceito, podemos pensar em sua existência independentemente da existência do recipiente que a contém. Por exemplo, um mergulhador nadando em alto mar está exposto ao peso gerado por uma coluna "imaginária" de líquido que existe sobre o mergulhador, desde a superfície do líquido até sua pele e a superfície do mar.

la massa da coluna líquida ($M$) pode ser calculado a partir de la densidade líquida ($\rho_w$) e o volume da coluna ($V$).
Para calcular la densidade líquida ($\rho_w$), utiliza-se a seguinte equação:
| $ \rho_w = \displaystyle\frac{ M }{ V }$ |
E para o volume da coluna ($V$), a equação é:
| $ V = S h $ |
Dessa forma, o valor de la massa da coluna líquida ($M$) é obtido por meio de:
| $ M = \rho_w S h $ |
Isso é válido desde que la altura da coluna líquida ($S$) permaneça constante ao longo de la altura da coluna ($h$).
A seção pode mudar em sua forma, mas não em sua superfície.
ID:(2207, 0)
Força da água na parte inferior da coluna
Nota 
Uma vez que o volume e, portanto, a massa da coluna são conhecidos, pode-se calcular a força que ela exerce em sua base. É importante notar que isso se aplica a líquidos considerados incompressíveis, o que significa que as camadas inferiores do líquido são supostas não serem comprimidas pelo peso das camadas acima delas.
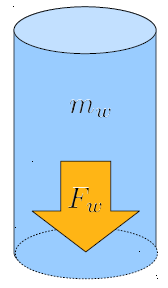
Esse princípio pode ser aplicado para calcular a força exercida por qualquer líquido, como água ou óleo, e é particularmente útil na engenharia hidráulica e na mecânica dos fluidos.
Dado que la massa da coluna líquida ($M$) depende de la densidade líquida ($\rho_w$), la altura da coluna líquida ($S$) e la altura da coluna ($h$) de acordo com a equação:
| $ M = \rho_w S h $ |
e la força da coluna ($F$) é representada com la aceleração gravitacional ($g$) por:
| $ F_g = m_g g $ |
então a expressão pode ser escrita da seguinte forma:
| $ F = S h \rho_w g $ |
.
ID:(2208, 0)
Introdução do conceito de pressão
Citar 
Na mecânica, descrevemos como corpos com massa definida se movem. No caso de um líquido, seu movimento não é uniforme e cada seção do líquido se move de forma diferente. No entanto, essas \\"seções\\" não têm uma massa definida, já que não são objetos definidos ou separados.
Para resolver essa questão, podemos segmentar o líquido em uma série de pequenos volumes separados e, se possível, estimar sua massa usando a densidade. Dessa forma, podemos introduzir a ideia de que as forças definem o movimento do líquido.
No entanto, os volumes são arbitrários em última instância, e o que acaba gerando o movimento é a força que atua na face do volume. Portanto, faz mais sentido introduzir o conceito de ERROR:10113,0 por tal ERROR:6002,0, que é chamado de la pressão da coluna de água ($p$).
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
ID:(46, 0)
Pressão da água na parte inferior da coluna
Exercício 
A La força da coluna ($F$) que atua sobre o fundo depende de la altura da coluna líquida ($S$) no sentido de que se esta última variar, a força também variará na mesma proporção. Nesse sentido, la força da coluna ($F$) e la altura da coluna líquida ($S$) não estão interligados de forma dependente; eles variam proporcionalmente. Faz sentido definir essa proporção como la pressão ($p$):

Como a la força da coluna ($F$) gerada por uma coluna de líquido de la altura da coluna ($h$), la altura da coluna líquida ($S$), la densidade líquida ($\rho_w$) e la aceleração gravitacional ($g$) é
| $ F = S h \rho_w g $ |
e a la pressão da coluna de água ($p$) é definida então como
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
temos que a la pressão da coluna de água ($p$) gerada por uma coluna de líquido é
| $ p = \rho_w g h $ |
Esta é a lei da pressão hidrostática, também conhecida como Lei de Pascal, principalmente atribuída a Blaise Pascal [1].
![]() [1] "Traité de l'équilibre des liqueurs" (Tratado sobre o Equilíbrio dos Líquidos), Blaise Pascal, 1663.
[1] "Traité de l'équilibre des liqueurs" (Tratado sobre o Equilíbrio dos Líquidos), Blaise Pascal, 1663.
ID:(2085, 0)
Soma da pressão da coluna e atmosfera
Equação 
Se considerarmos que a coluna está sob a influência de la pressão atmosférica ($p_0$), então a contribuição de la pressão atmosférica ($p_0$) deve ser somada a la pressão da coluna de água ($p$) da coluna, conforme mostrado aqui:

Quando calculamos la pressão da coluna de água ($p$) a uma determinada profundidade, é importante levar em consideração que a superfície do líquido está exposta a la pressão atmosférica ($p_0$), o que pode afetar o valor da pressão nesse ponto. Portanto, é necessário generalizar a equação para la pressão da coluna de água ($p$) para incluir não apenas a coluna de líquido la densidade líquida ($\rho_w$), la altura da coluna ($h$) e la aceleração gravitacional ($g$), mas também la pressão atmosférica ($p_0$):
| $ p_t = p_0 + \rho_w g h $ |
Não é sempre necessário considerar a pressão atmosférica na modelagem:
Em muitos casos, a pressão atmosférica está presente em todo o sistema, de modo que as diferenças de pressão não dependem dela.
ID:(2210, 0)
Conectando duas colunas de líquido
Script 
Ao conectar duas colunas de água com alturas diferentes em suas bases, é criada uma situação em que existe uma diferença de pressão ao longo do tubo conectado.
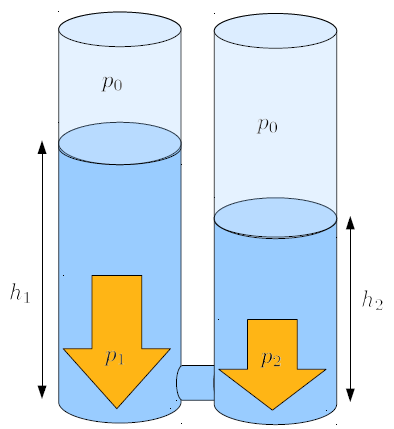
Esse arranjo nos permite estudar como a diferença de pressão gera um fluxo de líquido ao longo do tubo. Podemos pensar em um elemento de líquido com determinado comprimento e seção transversal igual à do tubo, e estimar a massa correspondente usando a densidade. Com a seção transversal, também podemos converter a diferença de pressão em uma diferença de forças e, assim, estudar como os volumes de líquidos são acelerados devido às diferenças de pressão.
ID:(933, 0)
Pressão hidrostática
Storyboard 
No caso de solo saturado, a porosidade está completamente preenchida com água. A presença de água implica massa adicional e a existência de pressão em função da profundidade. Ambos os fatores afetarão o comportamento do solo.
Variáveis
Cálculos
Cálculos
Equações
Dado que la massa da coluna líquida ($M$) depende de la densidade líquida ($\rho_w$), la altura da coluna líquida ($S$) e la altura da coluna ($h$) de acordo com a equa o:
e la força da coluna ($F$) representada com la aceleração gravitacional ($g$) por:
ent o a express o pode ser escrita da seguinte forma:
Dado que la massa da coluna líquida ($M$) depende de la densidade líquida ($\rho_w$), la altura da coluna líquida ($S$) e la altura da coluna ($h$) de acordo com a equa o:
e la força da coluna ($F$) representada com la aceleração gravitacional ($g$) por:
ent o a express o pode ser escrita da seguinte forma:
Como a la força da coluna ($F$) gerada por uma coluna de l quido de la altura da coluna ($h$), la altura da coluna líquida ($S$), la densidade líquida ($\rho_w$) e la aceleração gravitacional ($g$)
e a la pressão da coluna de água ($p$) definida ent o como
temos que a la pressão da coluna de água ($p$) gerada por uma coluna de l quido
Como a la força da coluna ($F$) gerada por uma coluna de l quido de la altura da coluna ($h$), la altura da coluna líquida ($S$), la densidade líquida ($\rho_w$) e la aceleração gravitacional ($g$)
e a la pressão da coluna de água ($p$) definida ent o como
temos que a la pressão da coluna de água ($p$) gerada por uma coluna de l quido
La massa da coluna líquida ($M$) pode ser calculado a partir de la densidade líquida ($\rho_w$) e o volume da coluna ($V$).
Para calcular la densidade líquida ($\rho_w$), utiliza-se a seguinte equa o:
E para o volume da coluna ($V$), a equa o :
Dessa forma, o valor de la massa da coluna líquida ($M$) obtido por meio de:
La massa da coluna líquida ($M$) pode ser calculado a partir de la densidade líquida ($\rho_w$) e o volume da coluna ($V$).
Para calcular la densidade líquida ($\rho_w$), utiliza-se a seguinte equa o:
E para o volume da coluna ($V$), a equa o :
Dessa forma, o valor de la massa da coluna líquida ($M$) obtido por meio de:
Se houver la diferença de pressão ($\Delta p$) entre dois pontos, conforme determinado pela equa o:
podemos usar la pressão da coluna de água ($p$), que definida como:
Isso resulta em:
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
Como la diferença de altura ($\Delta h$) :
la diferença de pressão ($\Delta p$) pode ser expressa como:
Exemplos
Para estudar o comportamento de l quidos, til introduzir o conceito de uma coluna de l quido. Essa coluna uma abstra o de um recipiente cil ndrico (por exemplo, uma proveta) com l quido, permitindo estudar a for a a que um objeto no interior dela est exposto.
Uma vez introduzido o conceito, podemos pensar em sua exist ncia independentemente da exist ncia do recipiente que a cont m. Por exemplo, um mergulhador nadando em alto mar est exposto ao peso gerado por uma coluna "imagin ria" de l quido que existe sobre o mergulhador, desde a superf cie do l quido at sua pele e a superf cie do mar.
la massa da coluna líquida ($M$) pode ser calculado a partir de la densidade líquida ($\rho_w$) e o volume da coluna ($V$).
Para calcular la densidade líquida ($\rho_w$), utiliza-se a seguinte equa o:
E para o volume da coluna ($V$), a equa o :
Dessa forma, o valor de la massa da coluna líquida ($M$) obtido por meio de:
Isso v lido desde que la altura da coluna líquida ($S$) permane a constante ao longo de la altura da coluna ($h$).
A se o pode mudar em sua forma, mas n o em sua superf cie.
Uma vez que o volume e, portanto, a massa da coluna s o conhecidos, pode-se calcular a for a que ela exerce em sua base. importante notar que isso se aplica a l quidos considerados incompress veis, o que significa que as camadas inferiores do l quido s o supostas n o serem comprimidas pelo peso das camadas acima delas.
Esse princ pio pode ser aplicado para calcular a for a exercida por qualquer l quido, como gua ou leo, e particularmente til na engenharia hidr ulica e na mec nica dos fluidos.
Dado que la massa da coluna líquida ($M$) depende de la densidade líquida ($\rho_w$), la altura da coluna líquida ($S$) e la altura da coluna ($h$) de acordo com a equa o:
e la força da coluna ($F$) representada com la aceleração gravitacional ($g$) por:
ent o a express o pode ser escrita da seguinte forma:
Na mec nica, descrevemos como corpos com massa definida se movem. No caso de um l quido, seu movimento n o uniforme e cada se o do l quido se move de forma diferente. No entanto, essas \\"se es\\" n o t m uma massa definida, j que n o s o objetos definidos ou separados.
Para resolver essa quest o, podemos segmentar o l quido em uma s rie de pequenos volumes separados e, se poss vel, estimar sua massa usando a densidade. Dessa forma, podemos introduzir a ideia de que as for as definem o movimento do l quido.
No entanto, os volumes s o arbitr rios em ltima inst ncia, e o que acaba gerando o movimento a for a que atua na face do volume. Portanto, faz mais sentido introduzir o conceito de ERROR:10113,0 por tal ERROR:6002,0, que chamado de la pressão da coluna de água ($p$).
A La força da coluna ($F$) que atua sobre o fundo depende de la altura da coluna líquida ($S$) no sentido de que se esta ltima variar, a for a tamb m variar na mesma propor o. Nesse sentido, la força da coluna ($F$) e la altura da coluna líquida ($S$) n o est o interligados de forma dependente; eles variam proporcionalmente. Faz sentido definir essa propor o como la pressão ($p$):
Como a la força da coluna ($F$) gerada por uma coluna de l quido de la altura da coluna ($h$), la altura da coluna líquida ($S$), la densidade líquida ($\rho_w$) e la aceleração gravitacional ($g$)
e a la pressão da coluna de água ($p$) definida ent o como
temos que a la pressão da coluna de água ($p$) gerada por uma coluna de l quido
Esta a lei da press o hidrost tica, tamb m conhecida como Lei de Pascal, principalmente atribu da a Blaise Pascal [1].
![]() [1] "Trait de l' quilibre des liqueurs" (Tratado sobre o Equil brio dos L quidos), Blaise Pascal, 1663.
[1] "Trait de l' quilibre des liqueurs" (Tratado sobre o Equil brio dos L quidos), Blaise Pascal, 1663.
Se considerarmos que a coluna est sob a influ ncia de la pressão atmosférica ($p_0$), ent o a contribui o de la pressão atmosférica ($p_0$) deve ser somada a la pressão da coluna de água ($p$) da coluna, conforme mostrado aqui:
Quando calculamos la pressão da coluna de água ($p$) a uma determinada profundidade, importante levar em considera o que a superf cie do l quido est exposta a la pressão atmosférica ($p_0$), o que pode afetar o valor da press o nesse ponto. Portanto, necess rio generalizar a equa o para la pressão da coluna de água ($p$) para incluir n o apenas a coluna de l quido la densidade líquida ($\rho_w$), la altura da coluna ($h$) e la aceleração gravitacional ($g$), mas tamb m la pressão atmosférica ($p_0$):
N o sempre necess rio considerar a press o atmosf rica na modelagem:
Em muitos casos, a press o atmosf rica est presente em todo o sistema, de modo que as diferen as de press o n o dependem dela.
Ao conectar duas colunas de gua com alturas diferentes em suas bases, criada uma situa o em que existe uma diferen a de press o ao longo do tubo conectado.
Esse arranjo nos permite estudar como a diferen a de press o gera um fluxo de l quido ao longo do tubo. Podemos pensar em um elemento de l quido com determinado comprimento e se o transversal igual do tubo, e estimar a massa correspondente usando a densidade. Com a se o transversal, tamb m podemos converter a diferen a de press o em uma diferen a de for as e, assim, estudar como os volumes de l quidos s o acelerados devido s diferen as de press o.
O volume da coluna ($V$) determinado por la altura da coluna líquida ($S$) e la altura da coluna ($h$) e calculado da seguinte forma:
O volume da coluna ($V$) determinado por la altura da coluna líquida ($S$) e la altura da coluna ($h$) e calculado da seguinte forma:
A La densidade líquida ($\rho_w$) calculada a partir de la massa da coluna líquida ($M$) e o volume da coluna ($V$) usando a equa o:
A La densidade líquida ($\rho_w$) calculada a partir de la massa da coluna líquida ($M$) e o volume da coluna ($V$) usando a equa o:
Usando la densidade líquida ($\rho_w$), la altura da coluna líquida ($S$) e la altura da coluna ($h$), voc pode calcular la massa da coluna líquida ($M$) com a f rmula:
Usando la densidade líquida ($\rho_w$), la altura da coluna líquida ($S$) e la altura da coluna ($h$), voc pode calcular la massa da coluna líquida ($M$) com a f rmula:
La força da coluna ($F$) calculado a partir de la altura da coluna líquida ($S$), la densidade líquida ($\rho_w$), la altura da coluna ($h$) e la aceleração gravitacional ($g$) usando:
La força da coluna ($F$) calculado a partir de la altura da coluna líquida ($S$), la densidade líquida ($\rho_w$), la altura da coluna ($h$) e la aceleração gravitacional ($g$) usando:
La pressão da coluna de água ($p$) calculado a partir de la força da coluna ($F$) e la altura da coluna líquida ($S$) da seguinte forma:
La pressão da coluna de água ($p$) calculado a partir de la força da coluna ($F$) e la altura da coluna líquida ($S$) da seguinte forma:
Se considerarmos a express o de la força da coluna ($F$) e a dividirmos por la altura da coluna líquida ($S$), obtemos la pressão da coluna de água ($p$). Nesse processo, simplificamos la altura da coluna líquida ($S$), de modo que n o dependa mais dele. A express o resultante a seguinte:
Se considerarmos a express o de la força da coluna ($F$) e a dividirmos por la altura da coluna líquida ($S$), obtemos la pressão da coluna de água ($p$). Nesse processo, simplificamos la altura da coluna líquida ($S$), de modo que n o dependa mais dele. A express o resultante a seguinte:
La pressão da coluna de água ($p$) com la densidade líquida ($\rho_w$), la altura da coluna ($h$), la aceleração gravitacional ($g$) e la pressão atmosférica ($p_0$) igual a:
La pressão da coluna de água ($p$) com la densidade líquida ($\rho_w$), la altura da coluna ($h$), la aceleração gravitacional ($g$) e la pressão atmosférica ($p_0$) igual a:
Quando duas colunas de l quido s o conectadas com la altura da coluna líquida 1 ($h_1$) e la altura da coluna líquida 2 ($h_2$), criada uma la diferença de altura ($\Delta h$), que calculada da seguinte forma:
A La diferença de altura ($\Delta h$) ir gerar a diferen a de press o que far o l quido fluir da coluna mais alta para a coluna mais baixa.
Quando duas colunas de l quido s o conectadas com la pressão na coluna 1 ($p_1$) e la pressão na coluna 2 ($p_2$), criada uma la diferença de pressão ($\Delta p$) que calculada de acordo com a seguinte f rmula:
la diferença de pressão ($\Delta p$) representa a diferen a de press o que far o l quido fluir da coluna mais alta para a coluna mais baixa.
A diferen a de altura, representada por la diferença de altura ($\Delta h$), implica que a press o em ambas as colunas diferente. Em particular, la diferença de pressão ($\Delta p$) uma fun o de la densidade líquida ($\rho_w$), la aceleração gravitacional ($g$) e la diferença de altura ($\Delta h$), da seguinte forma:
ID:(368, 0)
